상태공간 방정식과 전달함수

모든 선형 시불변 (LTI, linear time-invariant) 시스템은 다음과 같이 상태공간 방정식(state-space equation)으로 표현할 수 있다.

 

\[ \begin{align} \dot{\mathbf{x}}(t) &=A \mathbf{x}(t)+B\mathbf{u}(t) \tag{1} \\ \\ \mathbf{y}(t) &=C \mathbf{x}(t)+D \mathbf{u}(t), \ \ \ t \ge 0 \end{align} \]

 

여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\), \(\mathbf{u}(t) \in \mathbb{R}^p\), \( \mathbf{y}(t) \in \mathbb{R}^q\) 이고 \(A, B, C, D\) 는 상수 행렬이다.

 

 

이제 이 시스템의 해를 구해보자. 행렬지수함수의 정의에 의하면 다음 식이 성립한다.

 

\[ \frac{d}{dt} e^{At}=Ae^{At}=e^{At} A \tag{2} \]

 

식 (1)의 양변에 \(e^{-At}\) 를 곱하면

 

\[ e^{-At} \ \dot{\mathbf{x}}(t)=e^{-At} A \mathbf{x}(t)+e^{-At} B \mathbf{u}(t) \tag{3} \]

 

이 되는데, 식 (2)에 의하면 식 (3)은 다음과 같이 쓸 수 있다.

 

\[ \frac{d}{dt} \left( e^{-At} \mathbf{x}(t) \right)= e^{-At} B \mathbf{u}(t) \tag{4} \]

 

식 (4)의 양변을 적분하면,

 

\[ \left. e^{-At} \mathbf{x} (t) \right|_0^t= \int_0^t e^{-A \tau} B \mathbf{u}(\tau) \ d\tau \]

 

가 된다. 위 식을 풀면

 

\[ e^{-At} \mathbf{x}(t)- \mathbf{x}(0)= \int_0^t e^{-A \tau} B \mathbf{u} (\tau) \ d \tau \tag{5} \]

 

이 되므로 식 (1)의 해는 다음과 같이 구할 수 있다.

 

\[ \begin{align} \mathbf{x}(t) &= e^{At} \mathbf{x}(0)+ \int_0^t e^{A(t-\tau)} B \mathbf{u}( \tau) \ d \tau \tag{6} \\ \\ \mathbf{y}(t) &= Ce^{At} \mathbf{x}(0)+C \int_0^t e^{A(t-\tau)} B \mathbf{u}(\tau) \ d\tau +D\mathbf{u}(t) \end{align} \]

 

식 (6)에 의하면 시스템 (1)의 반응은 입력이 \(0\) 일 때(\(\mathbf{u}(t)=0\))의 반응인 제로-입력 반응과 초기값이 \(0\)일 때(\(\mathbf{x}(0)=0\))의 반응인 제로-상태 반응의 합으로 표현할 수 있다는 것을 알 수 있다 (https://pasus.tistory.com/59).

이와 같이 시간영역에서 직접 해를 구할 수 있지만 라플라스 변환(Laplace transform)을 이용하여 해를 구할 수도 있다. 식 (1)의 양변을 라플라스 변환하면 다음과 같이 된다.

 

\[ \begin{align} sX(s)- \mathbf{x}(0) &=AX(s)+BU(s)\tag{7} \\ \\ Y(s) &=CX(s)+DU(s) \end{align} \]

 

여기서 \(X(s)= \mathcal{L}[ \mathbf{x}(t)]\), \(U(s)=\mathcal{L}[\mathbf{u}(t)]\), \(Y(s)=\mathcal{L}[\mathbf{y}(t)]\) 이다. 식 (7)을 정리하면 다음과 같이 s-영역에서 해를 구할 수 있다.

 

\[ \begin{align} X(s) &= (sI-A)^{-1} \mathbf{x}(0)+(sI-A)^{-1} BU(s) \tag{8} \\ \\ Y(s) &=C(sI-A)^{-1} \mathbf{x}(0)+C(sI-A)^{-1} BU(s)+DU(s) \end{align} \]

 

만약 초기값이 모두 \(0\) 이라면, 즉 \(\mathbf{x}(0)=0\), 시스템 (1)의 입출력 관계식을 다음과 같이 쓸 수 있다.

 

\[ \begin{align} Y(s) &= C(sI-A)^{-1} BU(s)+DU(s) \tag{9} \\ \\ &= H(s)U(s) \end{align} \]

 

여기서 행렬 \(H(s)\) 를 시스템의 전달함수행렬(transfer-function matrix) 또는 전달행렬이라고 한다.

 

\[ H(s)=C(sI-A)^{-1} B+D \tag{10} \]

 

이제 식 (8)을 라플라스 역변환하면 \(\mathbf{x}(t)\) 를 계산할 수 있다.

 

\[ \begin{align} \mathbf{x}(t) &= \mathcal{L}^{-1} [X(s)] = \mathcal{L}^{-1} [(sI-A)^{-1} ] \mathbf{x}(0) \tag{11} \\ \\ & \ \ \ \ \ + \mathcal{L}^{-1} [(sI-A)^{-1} ]* \mathcal{L}^{-1} [BU(s)] \end{align} \]

 

여기서 \(*\) 기호는 컨볼루션(convolution)을 의미한다.

 

 

식 (10)에서 \(\mathcal{L}^{-1} [(sI-A)^{-1} ]\) 를 계산하기 앞서 행렬지수함수 \(e^{At}\) 의 라플라스 변환부터 계산해 보자. \(e^{At}\) 의 정의에 의하면 라플라스 변환은 다음과 같다.

 

\[ \begin{align} \mathcal{L}[e^{At} ] &= \mathcal{L} \left[ I+tA+ \frac{t^2}{2!} A^2+ \frac{t^3}{3!} A^3+ \cdots \right] \tag{12} \\ \\ &= \frac{1}{s} I+ \frac{1}{s^2} A+ \frac{1}{s^3} A^2+ \frac{1}{s^4} A^3 + \cdots \end{align} \]

 

식 (12)의 양변에 \(\frac{1}{s} A\) 를 곱하면 다음과 같다.

 

\[ \frac{1}{s} \mathcal{L}[e^{At} ] A= \frac{1}{s^2} A+ \frac{1}{s^3} A^2+ \frac{1}{s^4} A^3 + \cdots \tag{13} \]

 

이제 식 (13)에서 (12)를 빼면

 

\[ \mathcal{L}[e^{At} ]- \frac{1}{s} \mathcal{L}[e^{At} ]A= \frac{1}{s} I \tag{14} \]

 

이 되므로, \(\mathcal{L}[e^{At} ]\) 는 다음과 같이 계산된다.

 

\[ \begin{align} \mathcal{L}[e^{At} ] &= \frac{1}{s} \left( I- \frac{1}{s} A \right)^{-1}= \left[ s \left( I- \frac{1}{s} A \right) \right]^{-1} \tag{15} \\ \\ &=(sI-A)^{-1} \end{align} \]

 

식 (15)에 의하면 \(\mathcal{L}^{-1} [(sI-A)^{-1} ]=e^{At}\) 가 됨을 알 수 있다. 따라서 식 (11)은 다음과 같이 된다.

 

\[ \begin{align} \mathbf{x}(t) &=e^{At} \mathbf{x}(0)+ e^{At}*B \mathbf{u}(t) \tag{16} \\ \\ &=e^{At} \mathbf{x}(0)+ \int_0^t e^{A(t-\tau)} B \mathbf{u}( \tau) \ d\tau \\ \\ \mathbf{y}(t) &= Ce^{At} \mathbf{x}(0)+C \int_0^t e^{A(t-\tau)} B \mathbf{u}(\tau) \ d\tau +D \mathbf{u}(t) \\ \\ &= Ce^{At} \mathbf{x}(0)+ \int_0^t \left[ Ce^{A(t-\tau)} B+D \delta(t-\tau) \right] \mathbf{u}( \tau) \ d\tau \\ \\ &=Ce^{At} \mathbf{x}(0)+ \int_0^t h(t-\tau) \mathbf{u}(\tau) \ d\tau \end{align} \]

 

여기서 \(\delta (t)\) 는 디랙델타(Dirac-delta)함수이고 \(h(t)\) 를 임펄스반응행렬(impulse response matrix) 또는 임펄스행렬이라고 한다.

 

\[ h(t)=Ce^{At} B+D \delta (t) \tag{17} \]

 

식 (10)과 (17)에 의하면 시스템의 전달함수행렬과 임펄스반응행렬은 다음 관계가 있음을 알 수 있다.

 

\[ H(s)= \mathcal{L} [h(t)] \tag{18} \]

 

시스템을 수학적으로 표현하는 방법이 두가지가 있는데, 식 (1)은 상태공간 방정식으로 표현하는 방법이고, 식 (9)나 또는 식 (19)는 입출력의 관계식으로 표현하는 방법이다.

 

\[ \mathbf{y}(t)= \int_0^t h(t-\tau ) \mathbf{u}( \tau) \ d \tau \tag{19} \]

 

입출력의 관계식으로 표현하는 방법에서는 시스템의 초기값이 \(0\) 이라고 가정하며, 이 경우 시스템의 반응은 오로지 입력만의 영향을 받는 제로-상태 반응과 같다.

입력이 \(p\) 개 (\(\mathbf{u}(t) \in \mathbb{R}^p\)), 출력이 \(q\) 개 (\(\mathbf{y}(t) \in \mathbb{R}^q\))인 시스템에서 임펄스반응행렬은 다음과 같이 \(q \times p\) 행렬로 주어진다.

 

\[ h(t-\tau)= \begin{bmatrix} h_{11} (t-\tau) & h_{12} (t-\tau) & \cdots & h_{1p} (t-\tau) \\ h_{21} (t-\tau) & h_{22} (t-\tau) & \cdots & h_{2p} (t-\tau) \\ \vdots & \vdots & \ddots & \vdots \\ h_{q1} (t-\tau) & h_{q2} (t-\tau) & \cdots & h_{qp} (t-\tau) \end{bmatrix} \tag{20} \]

 

여기서 \(h_{ij} (t-\tau)\) 는 다른 입력단에서의 입력값이 모두 \(0\) 이고 시간 \(\tau\) 에서 \(j\) 번째 입력단에만 임펄스가 가해졌을 때 시간 \(t\) 에서 \(i\) 번째 출력단에서의 반응을 나타낸다.

 

 

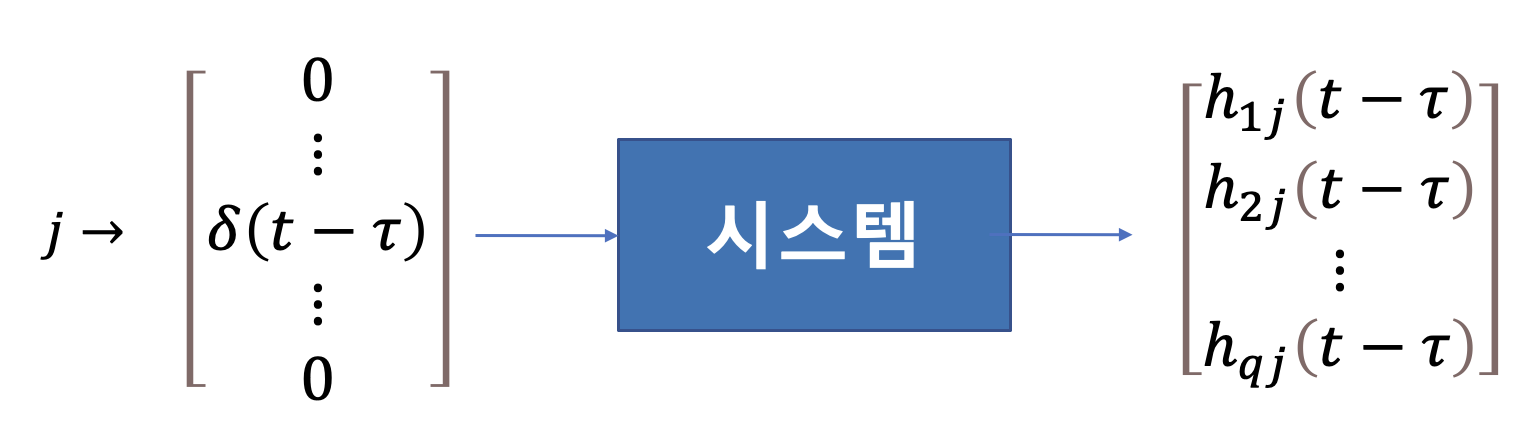
전달함수행렬도 다음과 같이 \(q \times p\) 행렬로 주어진다.

 

\[ H(s)= \begin{bmatrix} H_{11} (s) & H_{12} (s) & \cdots & H_{1p} (s) \\ H_{21} (s) & H_{22} (s) & \cdots & H_{2p} (s) \\ \vdots & \vdots & \ddots & \vdots \\ H_{q1} (s) & H_{q2} (s) & \cdots & H_{qp} (s) \end{bmatrix} \tag{21} \]

 

여기서 \(H_{ij} (s)\) 는 \(j\) 번째 입력에서 \(i\) 번째 출력으로의 전달함수이며 다음과 같이 계산된다.

 

\[ H_{ij} (s)= \mathcal{L}[h_{ij} (t)] \tag{22} \]

 

상태공간 방정식이 주어지면 식 (10)으로 전달행렬을 계산할 수 있다. 이와 반대로 전달행렬에서 상태공간 방정식을 계산할 수 있다면 그 행렬을 실현가능(realizable)하다고 하고 계산된 행렬 \(A, B, C, D\) 를 '실현(realization)' 이라고 한다.

\(H(s)\) 가 실현가능하기 위한 필요충분조건은 \(H(s)\) 가 '적절한 유리함수 행렬' (proper rational matrix)이어야 한다는 것이다. 유리함수란 다항식을 다항식으로 나눈 함수로 정의되며, 적절한 유리함수란 다항식 분모의 차수가 다항식 분자의 차수보다 크거나 같은 함수를 의미한다. \(H(s)\) 가 실현가능하다면 무수히 많은 행렬 \(A, B, C, D\) 를 구할 수 있다.