보통 제어기는 디지털 방식으로 구현되고 있다. 이 방식에서는 제어기의 출력도 디지털 신호이기 때문에 일정한 시간 간격에서만 사용할 수 있다. 즉 이산시간(discrete-time) 단계에서만 새로운 제어입력 값을 사용할 수 있다. 하지만 제어 대상 시스템이 연속시간(continuous-time) 시스템이라면 연속적인 입력이 필요하기 때문에 간헐적으로 계산되는 제어 입력을 사용할 수는 없다. 이 때 일반적으로 사용하는 방법은 다음 샘플링 시간까지 제어입력 값을 일정하게 유지시키는 것이다. 이를 0차홀드(ZOH, zero-order hold) 방식이라고 한다. 물론 더 복잡한 유형의 홀드 연산도 가능하지만, ZOH가 가장 널리 사용된다.
연속시간 (continuous-time) 선형 시불변 (LTI, linear time-invariant) 시스템은 다음과 같이 상태공간 방정식(state-space equation)으로 표현할 수 있다.
\[ \begin{align} & \dot{\mathbf{x}}(t)=A \mathbf{x}(t)+B \mathbf{u}(t) \tag{1} \\ \\ & \mathbf{y}(t)=C \mathbf{x}(t)+D \mathbf{u}(t) \end{align} \]
여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\), \(\mathbf{u}(t) \in \mathbb{R}^p\), \(\mathbf{y}(t) \in \mathbb{R}^q\) 이고 \(A, \ B, \ C, \ D\) 는 상수 행렬이다.
이제 시스템의 입력 \(\mathbf{u}(t)\) 가 시간 \(t=t_k\) 에서만 바뀌고, 시간 \(t_k \le t \lt t_{k+1}\)사이에서는 일정한 값으로 유지된다고 가정하자. 즉,
\[ \begin{align} \mathbf{u}(t)= \mathbf{u} (t_k ), \ \ \ \ \ t_k \le t \lt t_{k+1} \tag{2} \end{align} \]
여기서 \(T=t_{k+1}-t_k\) 는 샘플링 시간이고 \(\mathbf{u}(t_k )\) 는 시간 \(t=t_k\) 에서 \(\mathbf{u}(t)\) 값을 의미한다. \(k\) 는 시간스텝(time step)을 나타내는 인덱스로서 정수 값을 갖는다.

그러면 샘플링 구간 \(t \in [t_k, \ t_{k+1} )\) 에서 연속시간 시스템의 해를 구하면 다음과 같이 된다 (https://pasus.tistory.com/296).
\[ \begin{align} \mathbf{x}(t_{k+1} ) & =e^{AT} \mathbf{x}(t_k )+ \int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)} B \mathbf{u}(\tau) \ d \tau \tag{3} \\ \\ &=e^{AT} \mathbf{x}(t_k )+ \int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)} B \ d \tau \ \mathbf{u}(t_k ) \end{align} \]
위 식에서 적분변수를 \(\lambda =\tau-t_k\) 로 변환하면,
\[ \begin{align} \mathbf{x}(t_{k+1} ) &= e^{AT} \mathbf{x}(t_k )+ \int_0^{t_{k+1}-t_k} e^{A(t_{k+1}-t_k-\lambda)} B \ d \lambda \ \mathbf{u}(t_k ) \tag{4} \\ \\ &=e^{AT} \mathbf{x}(t_k )+ \int_0^T e^{A(T-\lambda)} B \ d\lambda \ \mathbf{u}(t_k ) \end{align} \]
이 된다. 다시 \(\tau=T-\lambda\) 로 변환하여 정리하면,
\[ \begin{align} \mathbf{x}(t_{k+1} ) &= e^{AT} \mathbf{x}(t_k )+ \int_T^0 e^{A \tau} B \ (-d \tau) \ \mathbf{u}(t_k ) \tag{5} \\ \\ &=e^{AT} \mathbf{x}(t_k )+ \int_0^T e^{A\tau} B \ d\tau \ \mathbf{u}(t_k ) \end{align} \]
이 된다. 이산시간 시스템의 기호를 따르기 위하여 다음과 같이 정의하면,
\[ \begin{align} \mathbf{x}_{k+1}= \mathbf{x}(t_{k+1} ), \ \ \ \mathbf{x}_k= \mathbf{x}(t_k ), \ \ \ \mathbf{u}_k=\mathbf{u}(t_k ) \tag{6} \end{align} \]
다음과 같이 연속시간 시스템 (1)의 이산시간 등가 모델(equivalent model)을 얻을 수 있다.
\[ \begin{align} \mathbf{x}_{k+1}= F \mathbf{x}_k+G \mathbf{u}_k \tag{7} \end{align} \]
여기서
\[ \begin{align} F &=e^{AT} \tag{8} \\ \\ G &= \int_0^T e^{A\tau } B \ d \tau \\ &=A^{-1} \left[ e^{A\tau} \right]_0^T B \\ &=A^{-1} [e^{AT}-I] B \end{align} \]
이다. 식 (8)에서는 \(A\) 의 역행렬이 존재함을 가정하였다.
식 (1)의 측정 모델은 동적운동이 없는 정적 시스템이기 때문에 다음과 같이 간단히 샘플링된 변환식을 구할 수 있다.
\[ \begin{align} \mathbf{y}_k=C \mathbf{x}_k+D \mathbf{u}_k \tag{9} \end{align} \]
여기서 \(\mathbf{y}_k= \mathbf{y}(t_k )\) 이다. 식 (7)과 (9)를 이산시간(discrete-time) 차분 방정식(difference equation)이라고 한다.
식 (8)을 테일러 시리즈(Taylor series)로 전개하면 다음과 같다.
\[ \begin{align} F &= e^{AT}=I+AT+ \frac{T^2}{2} A^2+ ⋯ \tag{10} \\ \\ G &= A^{-1} [e^{AT}-I]B \\ &=A^{-1} \left[ AT+ \frac{T^2}{2} A^2+⋯ \right] B \\ &= BT+ \frac{T^2}{2} AB + ⋯ \end{align} \]
만약 샘플링 시간 \(T\) 가 매우 작다면 위 식에서 \(T^2\) 이상은 절삭할 수 있다. 이를 오일러 근사 (Euler's approximation)라고 한다.
오일러 근사식은 식 (1)에서 미분을 다음과 같이 근사화하여 직접 구할 수도 있다.
\[ \begin{align} & \dot{\mathbf{x}}(t_k ) \approx \frac{ \mathbf{x}(t_{k+1} )- \mathbf{x}(t_k )}{T}=A \mathbf{x}(t_k )+B \mathbf{u}(t_k ) \tag{11} \\ \\ \to \ \ & \mathbf{x}(t_{k+1} )=(I+AT) \mathbf{x}(t_k )+BT \mathbf{u}(t_k ) \\ \\ \to \ \ & \mathbf{x}_{k+1}=(I+AT) \mathbf{x}_k+BT \mathbf{u}_k \end{align} \]
식 (11)에서 \(\dot{\mathbf{x}}(t_k )\) 을 근사화할 때 미래 시간과 현재 시간의 \(\mathbf{x}(t)\) 값을 이용(forward difference)했는데, 현재 시간과 과거 시간의 값을 이용(backward difference) 할 수도 있다.
\[ \begin{align} & \dot{\mathbf{x}}(t_k ) \approx \frac{ \mathbf{x}(t_k )- \mathbf{x}(t_{k-1} )}{T}=A \mathbf{x}(t_k )+B \mathbf{u}(t_k ) \tag{12} \\ \\ \to \ \ & \mathbf{x}(t_k )= AT \mathbf{x}(t_k )+ \mathbf{x}(t_{k-1}) + BT \mathbf{u}(t_k ) \\ \\ \to \ \ & \mathbf{x}_k=(I-AT)^{-1} \mathbf{x}_{k-1}+(I-AT)^{-1} BT \mathbf{u}_k \\ \\ & \ \ \ \ \ \approx (I+AT) \mathbf{x}_{k-1}+BT \mathbf{u}_k \end{align} \]
식 (12)에서 세번째 줄은 \(T\) 가 매우 작다는 가정하에서 성립한다. 식 (7) 또는 (11)과 식 (12)의 차이점은 제어입력 \(\mathbf{u}_k\) 가 가해지는 싯점에 있다. 식 (7) 또는 (11)에서는 \(\mathbf{x}_{k+1}\) 를 계산할 때 \(\mathbf{u}_k\) 가 적용된 반면 식 (12)에서는 \(\mathbf{x}_k\) 를 계산할 때 \(\mathbf{u}_k\) 가 적용되었다.
제어 분야에서는 식 (7) 또는 (11)의 형식이 일반적으로 사용되는 반면에, 기계학습 분야에서는 식 (12)의 형식이 사용되기도 한다.
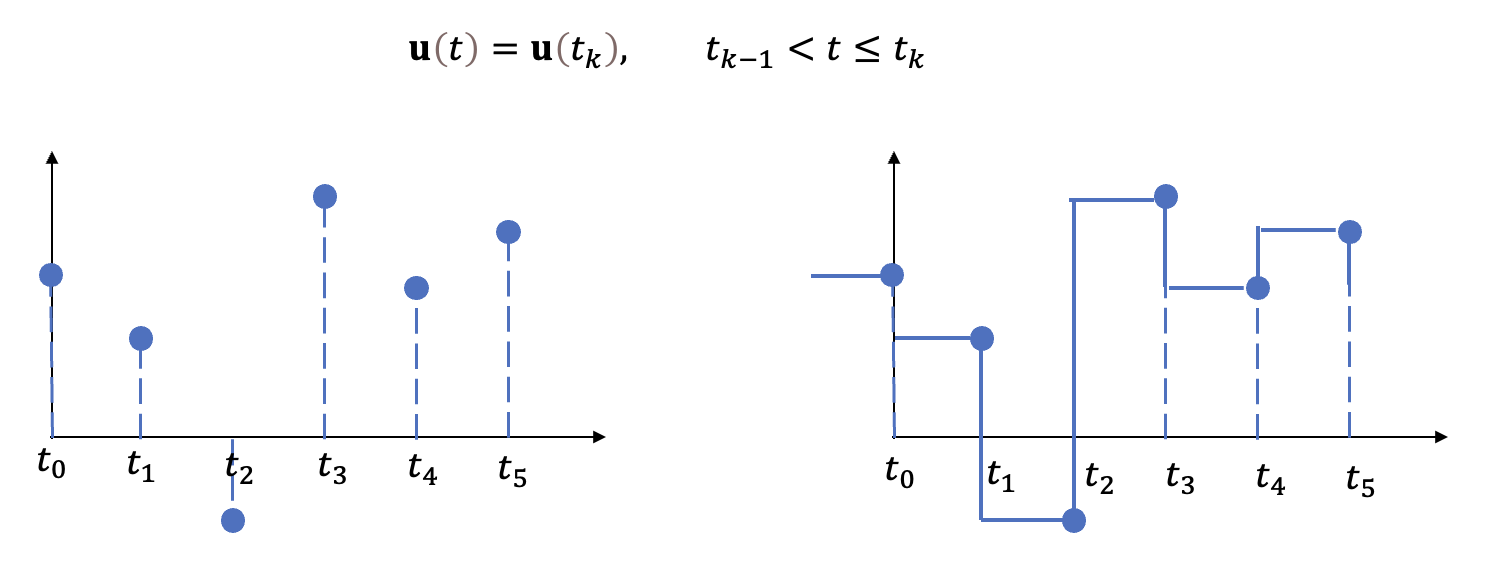
만약 시스템의 입력 \(\mathbf{u}(t)\) 가 시간 \(t_{k-1} \lt t \le t_k\) 사이에서는 일정한 값 \(\mathbf{u}(t)=\mathbf{u}(t_k )\) 로 유지된다고 가정하면, 식 (1)의 해는 다음과 같이 된다.
\[ \begin{align} \mathbf{x}(t_k ) &= e^{AT} \mathbf{x}(t_{k-1} )+ \int_{t_{k-1}}^{t_k} e^{A(t_k-\tau)} B \ \mathbf{u}(\tau) \ d\tau \tag{13} \\ \\ &=e^{AT} \mathbf{x}(t_{k-1} )+\int_{t_{k-1}}^{t_k} e^{A(t_k-\tau)} B \ d \tau \ \mathbf{u}(t_k ) \end{align} \]
그러면 연속시간 시스템 (1)의 이산시간 등가 모델은 다음과 같다.
\[ \begin{align} \mathbf{x}_k=F \mathbf{x}_{k-1}+G \mathbf{u}_k \tag{14} \end{align} \]
여기서 \(F\) 와 \(G\) 는 식 (8)과 동일하다. 식 (14)는 식 (12)와 마찬가지로 제어입력이 가해지는 싯점이 식 (7) 또는 (11)과 차이가 있다.
지금까지 ZOH에 의한 등가 이산화 방법에 대해 설명했다. 이 방법은 샘플링 순간에 정확한 이산시간 모델을 제공한다. 이밖에 연속시간 전달함수(transfer function)를 이산시간 등가 함수로 변환하는 방법도 있다.
'유도항법제어 > 비행제어' 카테고리의 다른 글
| [Continuous-Time] 제어가능한 부분공간 (0) | 2024.07.23 |
|---|---|
| [Continuous-Time] 제어가능성 (Controllability) (0) | 2024.07.16 |
| 근궤적법 (Root locus method)에서 K→∞ 일 때의 근 (0) | 2023.11.03 |
| 상태공간 방정식과 전달함수 (0) | 2023.09.22 |
| 상태천이행렬 (State Transition Matrix) 과 Floquet 정리 (0) | 2023.06.30 |




댓글