[PX4] 멀티콥터 자세 명령

PX4의 위치 제어기에서는 원하는 궤적(desired trajectory) 정보를 이용하여 추력 벡터를 계산한다.

 

 

관성 좌표계 $\{i\}$ 로 표현된 추력 벡터는 별도로 주어지는 방위각(azimuth angle) 명령 ${\psi }_{cmd}$ 와 함께 자세 명령(attitude command) 계산 모듈로 보내져서 쿼터니언 ${\mathbf{q}}_{cmd}$ 로 파라미터화된 자세 명령을 생성하게 된다.

 

 

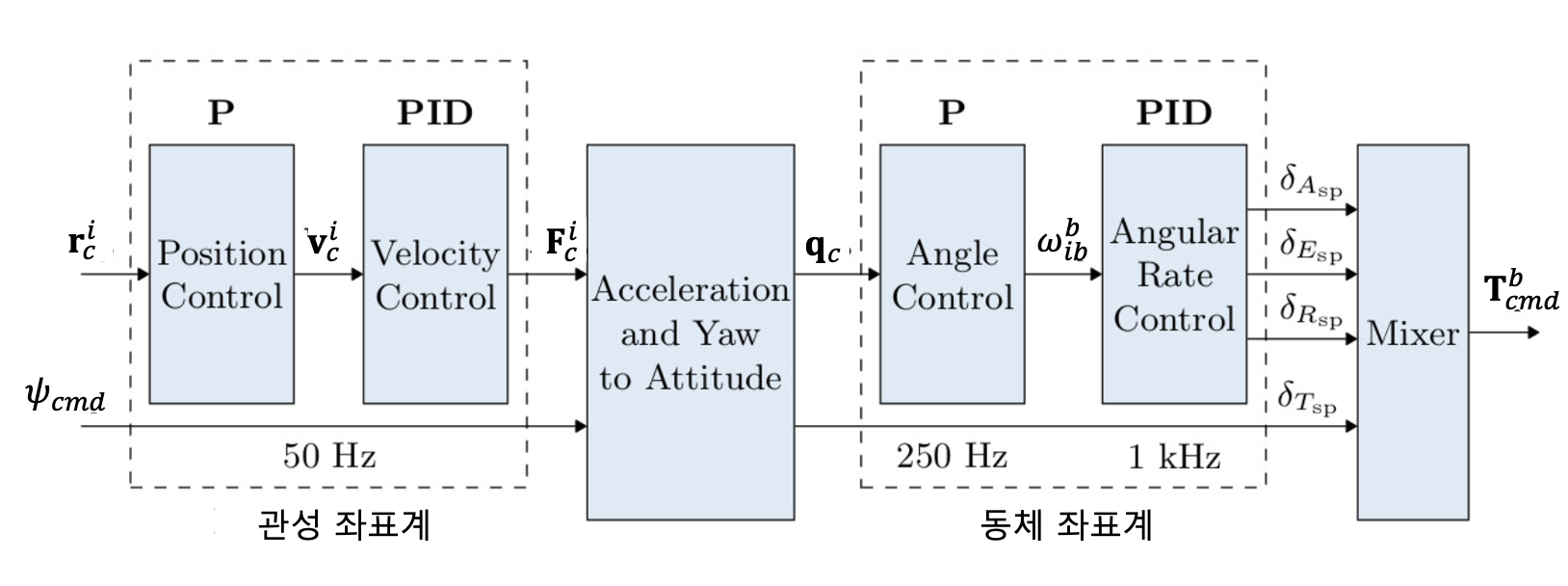
쿼터니언 ${\mathbf{q}}_{cmd}$ 를 계산하기 위해서는 먼저 관성 좌표계 $\{i\}$ 에 대해서 동체 좌표계 $\{b\}$ 가 취해야 할 목표 좌표계를 구해야 하는데 이 좌표계를 $\{d\}$ 라고 하자. 그러면 ${\mathbf{q}}_{cmd}={\mathbf{q}}_d^i$ 가 되며 자세 제어기의 목적은 $\{b\}=\{d\}$ 가 되도록 하는 것이다.

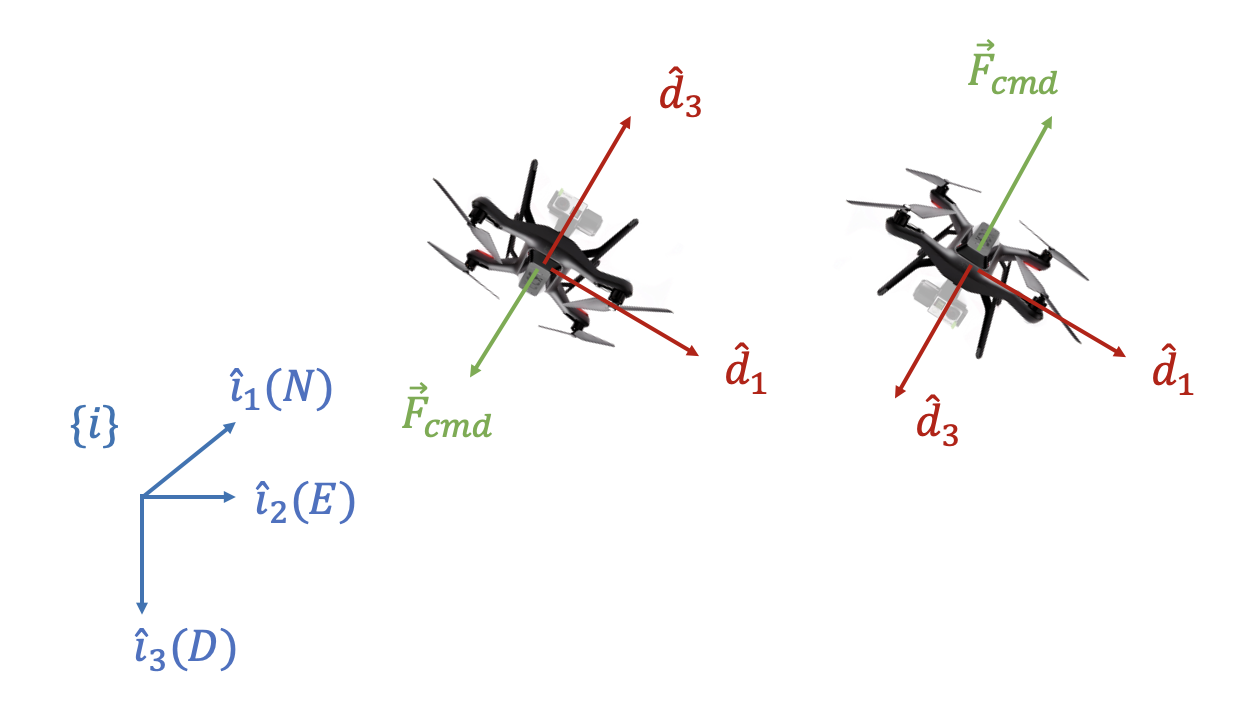
쿼터니언 ${\mathbf{q}}_d^i$ 는 방향코사인행렬(DCM) $C_d^i$ 를 계산한 후 변환하는 방법을 통해서 구하도록 한다. 먼저 좌표계 $\{d\}$ 의 ${\hat{d}}_3$ 축은 추력 벡터 ${\overrightarrow{F}}_{cmd}$ 의 반대 방향이어야 하므로 ${\hat{d}}_3$ 를 다음과 같이 정한다.

 

$$\begin{array}{r}\text{(1)}& & {\hat{d}}_3=-\frac{{\overrightarrow{F}}_{cmd}}{\Vert {\overrightarrow{F}}_{cmd}{\Vert }_2}\\ \to & {\mathbf{d}}_3^i=-\frac{{\mathbf{F}}_{cmd}^i}{\Vert {\mathbf{F}}_{cmd}^i{\Vert }_2}\end{array}$$

 

만약 추력이 $0$ 이라면 ${\hat{d}}_3={\hat{i}}_3$ 로 놓는다. 또는 ${\mathbf{d}}_3^i=[001{]}^T$ 로 놓는다. 방위각 명령 ${\psi }_{cmd}$ 는 3-2-1 오일러각 좌표변환 방법에 의해서 주어지는 첫번째 각, 즉 관성 좌표계의 ${\hat{i}}_3$ 축을 중심으로 한 회전각이므로 이를 반영하기 위해서 ${\hat{i}}_3$ 축을 중심으로 ${\psi }_{cmd}$ 만큼 좌표계 $\{i\}$ 를 회전시킨다. 이 때 변환된 임시 좌표계 $\{c\}$ 라고 하자.

 

 

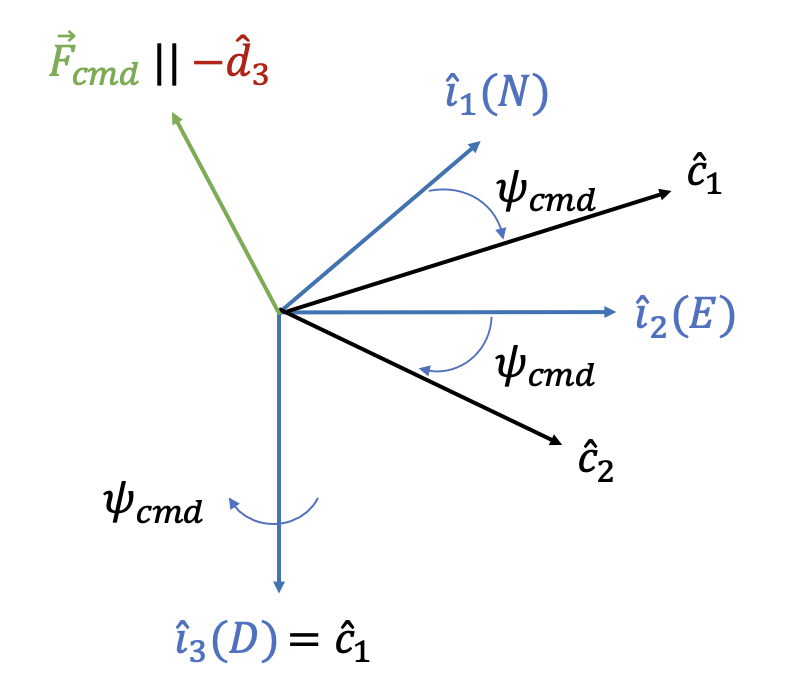
좌표계 $\{c\}$ 의 ${\hat{c}}_2$ 축은 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(2)}& {\mathbf{c}}_2^i& =C_c^i{\mathbf{c}}_2^c\\ & =\left[\begin{array}{ccc}\cos {\psi }_{cmd}& -\sin {\psi }_{cmd}& 0\\ \sin {\psi }_{cmd}& \cos {\psi }_{cmd}& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]\\ \\ & =\left[\begin{array}{c}-\sin {\psi }_{cmd}\\ \cos {\psi }_{cmd}\\ 0\end{array}\right]\end{array}$$

 

그런 다음 ${\hat{d}}_1$ 축을 다음과 같이 정의한다.

 

$$\begin{array}{r}\text{(3)}& & {\hat{d}}_1={\hat{c}}_2\times {\hat{d}}_3\\ \to & {\mathbf{d}}_1^i=[{\mathbf{c}}_2^i\times ]{\mathbf{d}}_3^i\end{array}$$

 

 

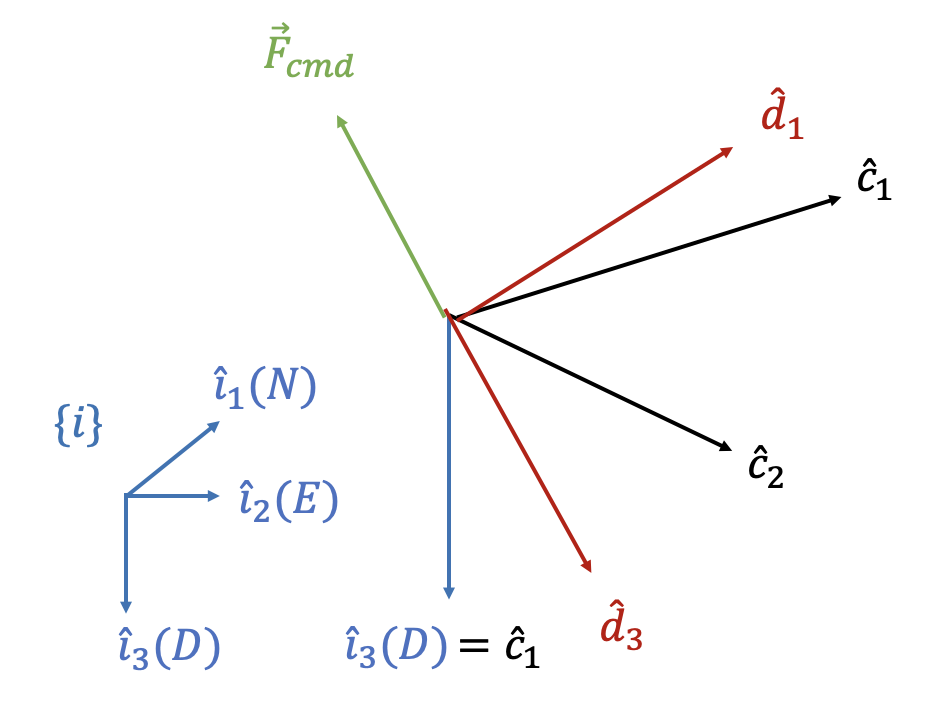
만약 ${\hat{d}}_3$ 축이 ${\hat{i}}_1-{\hat{i}}_2$ 평면에 있다면, 즉 ${\hat{d}}_3\cdot {\hat{i}}_3=0$ 이면 ${\hat{d}}_1={\hat{i}}_3$ 으로 놓는다.

 

 

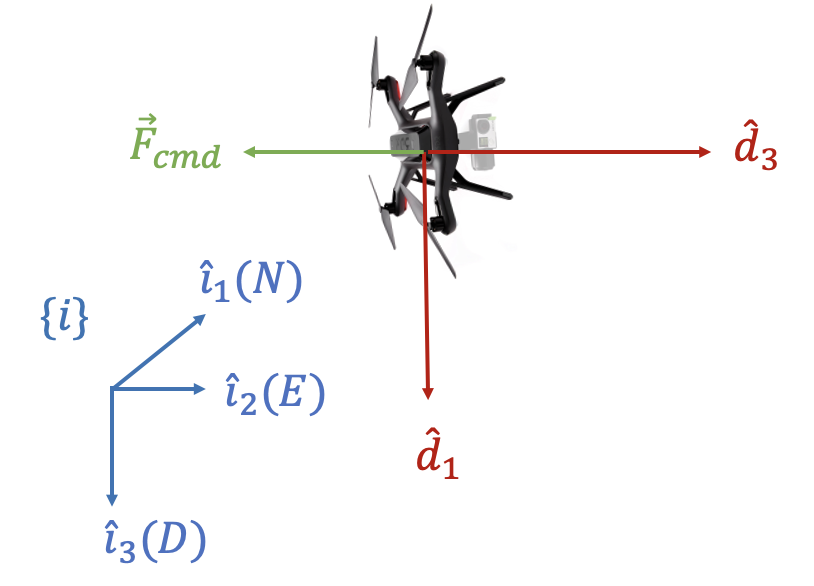
또한 만약 추력벡터가 아래 방향을 향하고 있으면, 즉 ${\hat{d}}_3\cdot {\hat{i}}_3<0$ 이면 식 (1)에서 계산된 ${\hat{d}}_1$ 대신에 ${\hat{d}}_1\leftarrow -{\hat{d}}_1$ 를 사용한다. 이유는 멀티콥터가 배면 비행을 할 때도 ${\hat{d}}_1$ 축을 같은 방향으로 유지하기 위해서다.

 

 

마지막으로 ${\hat{d}}_2$ 축은 오른손 법칙에 의해서 다음과 같이 정해진다.

 

$$\begin{array}{r}\text{(4)}& & {\hat{d}}_2={\hat{d}}_3\times {\hat{d}}_1\\ \to & {\mathbf{d}}_2^i=[{\mathbf{d}}_3^i\times ]{\mathbf{d}}_1^i\end{array}$$

 

식 (1), (3), (4)에서 구한 ${\mathbf{d}}_1^i,{\mathbf{d}}_2^i,{\mathbf{d}}_3^i$ 를 이용하면, 좌표계 $\{i\}$ 에서 좌표계 $\{d\}$ 로의 DCM $C_d^i$ 를 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(5)}& C_d^i& =\left[\begin{array}{ccc}{\hat{i}}_1\cdot {\hat{d}}_1& {\hat{i}}_1\cdot {\hat{d}}_2& {\hat{i}}_1\cdot {\hat{d}}_3\\ {\hat{i}}_2\cdot {\hat{d}}_1& {\hat{i}}_2\cdot {\hat{d}}_2& {\hat{i}}_2\cdot {\hat{d}}_3\\ {\hat{i}}_3\cdot {\hat{d}}_1& {\hat{i}}_3\cdot {\hat{d}}_2& {\hat{i}}_3\cdot {\hat{d}}_3\end{array}\right]\\ & =\left[\begin{array}{ccc}{\mathbf{d}}_1^i& {\mathbf{d}}_2^i& {\mathbf{d}}_3^i\end{array}\right]\end{array}$$

 

마지막으로 DCM과 쿼티니언 변환 관계식을 이용하여 다음과 같이 ${\mathbf{q}}_{cmd}={\mathbf{q}}_d^i$ 를 계산할 수 있다.

 

$$\begin{array}{}\text{(6)}& {\mathbf{q}}_{cmd}={\mathbf{q}}_d^i=\left[\begin{array}{c}\frac{1}{2}\sqrt{1+tr(C_d^i)}\\ \frac{C_{32}-C_{23}}{4q_0}\\ \frac{C_{13}-C_{31}}{4q_0}\\ \frac{C_{21}-C_{12}}{4q_0}\end{array}\right]\end{array}$$