상태공간 방정식과 전달함수

모든 선형 시불변 (LTI, linear time-invariant) 시스템은 다음과 같이 상태공간 방정식(state-space equation)으로 표현할 수 있다.

 

$$\begin{array}{r}\text{(1)}& \dot{\mathbf{x}}(t)& =A\mathbf{x}(t)+B\mathbf{u}(t)\\ \mathbf{y}(t)& =C\mathbf{x}(t)+D\mathbf{u}(t),t\ge 0\end{array}$$

 

여기서 $\mathbf{x}(t)\in {\mathbb{R}}^n$, $\mathbf{u}(t)\in {\mathbb{R}}^p$, $\mathbf{y}(t)\in {\mathbb{R}}^q$ 이고 $A,B,C,D$ 는 상수 행렬이다.

 

 

이제 이 시스템의 해를 구해보자. 행렬지수함수의 정의에 의하면 다음 식이 성립한다.

 

$$\begin{array}{}\text{(2)}& \frac{d}{dt}{e}^{At}=A{e}^{At}=e^{At}A\end{array}$$

 

식 (1)의 양변에 $e^{-At}$ 를 곱하면

 

$$\begin{array}{}\text{(3)}& e^{-At}\dot{\mathbf{x}}(t)=e^{-At}A\mathbf{x}(t)+e^{-At}B\mathbf{u}(t)\end{array}$$

 

이 되는데, 식 (2)에 의하면 식 (3)은 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(4)}& \frac{d}{dt}(e^{-At}\mathbf{x}(t))=e^{-At}B\mathbf{u}(t)\end{array}$$

 

식 (4)의 양변을 적분하면,

 

$${e^{-At}\mathbf{x}(t)|}_0^t={\int }_0^t{e}^{-A\tau }B\mathbf{u}(\tau )d\tau$$

 

가 된다. 위 식을 풀면

 

$$\begin{array}{}\text{(5)}& e^{-At}\mathbf{x}(t)-\mathbf{x}(0)={\int }_0^t{e}^{-A\tau }B\mathbf{u}(\tau )d\tau \end{array}$$

 

이 되므로 식 (1)의 해는 다음과 같이 구할 수 있다.

 

$$\begin{array}{r}\text{(6)}& \mathbf{x}(t)& =e^{At}\mathbf{x}(0)+{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau \\ \mathbf{y}(t)& =C{e}^{At}\mathbf{x}(0)+C{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau +D\mathbf{u}(t)\end{array}$$

 

식 (6)에 의하면 시스템 (1)의 반응은 입력이 $0$ 일 때($\mathbf{u}(t)=0$)의 반응인 제로-입력 반응과 초기값이 $0$일 때($\mathbf{x}(0)=0$)의 반응인 제로-상태 반응의 합으로 표현할 수 있다는 것을 알 수 있다 (https://pasus.tistory.com/59).

이와 같이 시간영역에서 직접 해를 구할 수 있지만 라플라스 변환(Laplace transform)을 이용하여 해를 구할 수도 있다. 식 (1)의 양변을 라플라스 변환하면 다음과 같이 된다.

 

$$\begin{array}{r}\text{(7)}& sX(s)-\mathbf{x}(0)& =AX(s)+BU(s)\\ Y(s)& =CX(s)+DU(s)\end{array}$$

 

여기서 $X(s)=\mathcal{L}[\mathbf{x}(t)]$, $U(s)=\mathcal{L}[\mathbf{u}(t)]$, $Y(s)=\mathcal{L}[\mathbf{y}(t)]$ 이다. 식 (7)을 정리하면 다음과 같이 s-영역에서 해를 구할 수 있다.

 

$$\begin{array}{r}\text{(8)}& X(s)& =(sI-A{)}^{-1}\mathbf{x}(0)+(sI-A{)}^{-1}BU(s)\\ Y(s)& =C(sI-A{)}^{-1}\mathbf{x}(0)+C(sI-A{)}^{-1}BU(s)+DU(s)\end{array}$$

 

만약 초기값이 모두 $0$ 이라면, 즉 $\mathbf{x}(0)=0$, 시스템 (1)의 입출력 관계식을 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(9)}& Y(s)& =C(sI-A{)}^{-1}BU(s)+DU(s)\\ & =H(s)U(s)\end{array}$$

 

여기서 행렬 $H(s)$ 를 시스템의 전달함수행렬(transfer-function matrix) 또는 전달행렬이라고 한다.

 

$$\begin{array}{}\text{(10)}& H(s)=C(sI-A{)}^{-1}B+D\end{array}$$

 

이제 식 (8)을 라플라스 역변환하면 $\mathbf{x}(t)$ 를 계산할 수 있다.

 

$$\begin{array}{r}\text{(11)}& \mathbf{x}(t)& ={\mathcal{L}}^{-1}[X(s)]={\mathcal{L}}^{-1}[(sI-A{)}^{-1}]\mathbf{x}(0)\\ & +{\mathcal{L}}^{-1}[(sI-A{)}^{-1}]\ast {\mathcal{L}}^{-1}[BU(s)]\end{array}$$

 

여기서 $\ast$ 기호는 컨볼루션(convolution)을 의미한다.

 

 

식 (10)에서 ${\mathcal{L}}^{-1}[(sI-A{)}^{-1}]$ 를 계산하기 앞서 행렬지수함수 $e^{At}$ 의 라플라스 변환부터 계산해 보자. $e^{At}$ 의 정의에 의하면 라플라스 변환은 다음과 같다.

 

$$\begin{array}{r}\text{(12)}& \mathcal{L}[e^{At}]& =\mathcal{L}[I+tA+\frac{t^2}{2!}{A}^2+\frac{t^3}{3!}{A}^3+\cdots ]\\ & =\frac{1}{s}I+\frac{1}{s^2}A+\frac{1}{s^3}{A}^2+\frac{1}{s^4}{A}^3+\cdots \end{array}$$

 

식 (12)의 양변에 $\frac{1}{s}A$ 를 곱하면 다음과 같다.

 

$$\begin{array}{}\text{(13)}& \frac{1}{s}\mathcal{L}[e^{At}]A=\frac{1}{s^2}A+\frac{1}{s^3}{A}^2+\frac{1}{s^4}{A}^3+\cdots \end{array}$$

 

이제 식 (13)에서 (12)를 빼면

 

$$\begin{array}{}\text{(14)}& \mathcal{L}[e^{At}]-\frac{1}{s}\mathcal{L}[e^{At}]A=\frac{1}{s}I\end{array}$$

 

이 되므로, $\mathcal{L}[e^{At}]$ 는 다음과 같이 계산된다.

 

$$\begin{array}{r}\text{(15)}& \mathcal{L}[e^{At}]& =\frac{1}{s}{(I-\frac{1}{s}A)}^{-1}={\left[s(I-\frac{1}{s}A)\right]}^{-1}\\ & =(sI-A{)}^{-1}\end{array}$$

 

식 (15)에 의하면 ${\mathcal{L}}^{-1}[(sI-A{)}^{-1}]=e^{At}$ 가 됨을 알 수 있다. 따라서 식 (11)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(16)}& \mathbf{x}(t)& =e^{At}\mathbf{x}(0)+e^{At}\ast B\mathbf{u}(t)\\ & =e^{At}\mathbf{x}(0)+{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau \\ \\ \mathbf{y}(t)& =C{e}^{At}\mathbf{x}(0)+C{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau +D\mathbf{u}(t)\\ \\ & =C{e}^{At}\mathbf{x}(0)+{\int }_0^t[C{e}^{A(t-\tau )}B+D\delta (t-\tau )]\mathbf{u}(\tau )d\tau \\ \\ & =C{e}^{At}\mathbf{x}(0)+{\int }_0^{t}h(t-\tau )\mathbf{u}(\tau )d\tau \end{array}$$

 

여기서 $\delta (t)$ 는 디랙델타(Dirac-delta)함수이고 $h(t)$ 를 임펄스반응행렬(impulse response matrix) 또는 임펄스행렬이라고 한다.

 

$$\begin{array}{}\text{(17)}& h(t)=C{e}^{At}B+D\delta (t)\end{array}$$

 

식 (10)과 (17)에 의하면 시스템의 전달함수행렬과 임펄스반응행렬은 다음 관계가 있음을 알 수 있다.

 

$$\begin{array}{}\text{(18)}& H(s)=\mathcal{L}[h(t)]\end{array}$$

 

시스템을 수학적으로 표현하는 방법이 두가지가 있는데, 식 (1)은 상태공간 방정식으로 표현하는 방법이고, 식 (9)나 또는 식 (19)는 입출력의 관계식으로 표현하는 방법이다.

 

$$\begin{array}{}\text{(19)}& \mathbf{y}(t)={\int }_0^{t}h(t-\tau )\mathbf{u}(\tau )d\tau \end{array}$$

 

입출력의 관계식으로 표현하는 방법에서는 시스템의 초기값이 $0$ 이라고 가정하며, 이 경우 시스템의 반응은 오로지 입력만의 영향을 받는 제로-상태 반응과 같다.

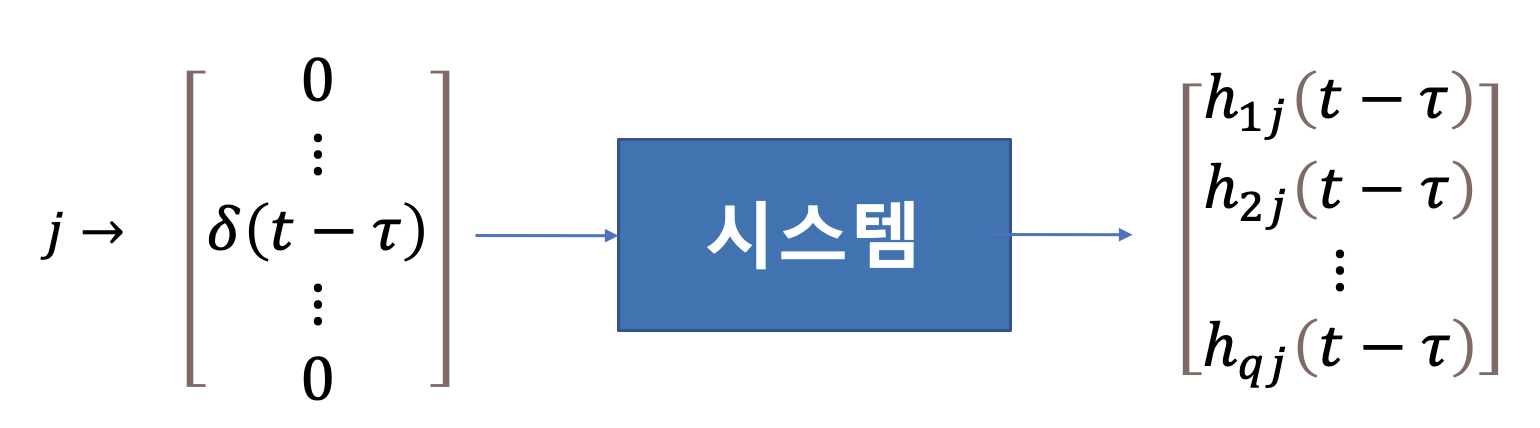
입력이 $p$ 개 ($\mathbf{u}(t)\in {\mathbb{R}}^p$), 출력이 $q$ 개 ($\mathbf{y}(t)\in {\mathbb{R}}^q$)인 시스템에서 임펄스반응행렬은 다음과 같이 $q\times p$ 행렬로 주어진다.

 

$$\begin{array}{}\text{(20)}& h(t-\tau )=\left[\begin{array}{cccc}{h}_{11}(t-\tau )& h_{12}(t-\tau )& \cdots & h_{1p}(t-\tau )\\ h_{21}(t-\tau )& h_{22}(t-\tau )& \cdots & h_{2p}(t-\tau )\\ ⋮& ⋮& \ddots & ⋮\\ h_{q1}(t-\tau )& h_{q2}(t-\tau )& \cdots & h_{qp}(t-\tau )\end{array}\right]\end{array}$$

 

여기서 $h_{ij}(t-\tau )$ 는 다른 입력단에서의 입력값이 모두 $0$ 이고 시간 $\tau$ 에서 $j$ 번째 입력단에만 임펄스가 가해졌을 때 시간 $t$ 에서 $i$ 번째 출력단에서의 반응을 나타낸다.

 

 

전달함수행렬도 다음과 같이 $q\times p$ 행렬로 주어진다.

 

$$\begin{array}{}\text{(21)}& H(s)=\left[\begin{array}{cccc}{H}_{11}(s)& H_{12}(s)& \cdots & H_{1p}(s)\\ H_{21}(s)& H_{22}(s)& \cdots & H_{2p}(s)\\ ⋮& ⋮& \ddots & ⋮\\ H_{q1}(s)& H_{q2}(s)& \cdots & H_{qp}(s)\end{array}\right]\end{array}$$

 

여기서 $H_{ij}(s)$ 는 $j$ 번째 입력에서 $i$ 번째 출력으로의 전달함수이며 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(22)}& H_{ij}(s)=\mathcal{L}[h_{ij}(t)]\end{array}$$

 

상태공간 방정식이 주어지면 식 (10)으로 전달행렬을 계산할 수 있다. 이와 반대로 전달행렬에서 상태공간 방정식을 계산할 수 있다면 그 행렬을 실현가능(realizable)하다고 하고 계산된 행렬 $A,B,C,D$ 를 '실현(realization)' 이라고 한다.

$H(s)$ 가 실현가능하기 위한 필요충분조건은 $H(s)$ 가 '적절한 유리함수 행렬' (proper rational matrix)이어야 한다는 것이다. 유리함수란 다항식을 다항식으로 나눈 함수로 정의되며, 적절한 유리함수란 다항식 분모의 차수가 다항식 분자의 차수보다 크거나 같은 함수를 의미한다. $H(s)$ 가 실현가능하다면 무수히 많은 행렬 $A,B,C,D$ 를 구할 수 있다.