관성좌표계의 원점 \(O\) 에 대한 파티클 시스템의 총 각운동량 \(\vec{H}_O\) 를 다음과 같이 정의한 바 있다.
\[ \vec{H}_O= \sum_{j=1}^n \vec{r}_j \times m_j \vec{v}_j \tag{1} \]
여기서 \(\vec{v}_j\) 는 파티클 \(j\) 의 속도로서 \(\vec{v}_j= \frac{^i d\vec{r}_j}{dt}\) 이다.
임의의 점 \(A\) 에 대한 파티클 시스템의 총 각운동량 \(\vec{H}_A\) 는 다음과 같이 정의한다.
\[ \vec{H}_A = \sum_{j=1}^n \vec{r}_{j/A} \times m_j \vec{v}_j \tag{2} \]
여기서 \(\vec{r}_{j/A}\) 는 점 \(A\) 에서 파티클 \(j\) 까지의 위치벡터다. 주의할 점은 속도는 여전히 \(\vec{v}_j= \frac{^i d\vec{r}_j}{dt}\) 로서 관성좌표계의 원점 \(O\) 에 대한 파티클 \(j\)의 위치벡터 \(\vec{r}_j\) 를 관성좌표계에서 미분한 속도라는 것이다.

점 \(A\) 에 대한 파티클 시스템의 총 각운동량 \(\vec{H}_A^\prime\) 를 다음과 같이 정의하기도 한다.
\[ \vec{H}_A^\prime= \sum_{j=1}^n \vec{r}_{j/A} \times m_j \vec{v}_{j/A} \tag{3} \]
여기서 \(\vec{v}_{j/A}\) 는 점 \(A\) 에 대한 파티클 \(j\) 의 상대속도로서 \(\vec{v}_{j/A}= \frac{^id \vec{r}_{j/A}}{dt}\) 이다. 일반적으로 \(\vec{H}_A \ne \vec{H}_A^\prime\) 이지만 점 \(A\) 가 시스템의 질량중심 \(G\) 라면 두 각운동량은 같다.
\[ \vec{H}_G= \vec{H}_G^\prime \tag{4} \]
먼저 이를 증명해 보기로 하자. 식 (2)로부터 질량중심G에 대한 파티클 시스템의 총 각운동량 \(\vec{H}_G\) 는 다음과 같다.
\[ \begin{align} \vec{H}_G &= \sum_{j=1}^n \vec{r}_{j/G} \times m_j \frac{^i d \vec{r}_j}{dt} \tag{5} \\ \\ &= \sum_{j=1}^n \vec{r}_{j/G} \times m_j \frac{^i d}{dt} \left( \vec{r}_G + \vec{r}_{j/G} \right) \\ \\ &= \sum_{j=1}^n \vec{r}_{j/G} \times m_j \frac{^i d \vec{r}_G}{dt} + \sum_{j=1}^n \vec{r}_{j/G} \times m_j \frac{ ^i d\vec{r}_{j/G}}{dt} \end{align} \]
위 식에서 점 \(G\) 는 질량중심이므로,
\[ \sum_{j=1}^n \vec{r}_{j /G} \times m_j \frac{^i d \vec{r}_G}{dt}= \left( \sum_{j=1}^n m_j \vec{r}_{j /G} \right) \times \frac{ ^i d \vec{r}_G}{dt}=0 \tag{6} \]
이 된다. 따라서 식 (5)는 식 (3)의 정의에 의해서
\[ \vec{H}_G = \sum_{j=1}^n \vec{r}_{j /G} \times m_j \frac{^id \vec{r}_{j /G}}{dt}= \vec{H}_G^\prime \tag{7} \]
가 된다.
이제 임의의 점 \(A\) 에 대한 시스템의 총 각운동량 식 (2)를 미분해 보자.
\[ \frac{^i d \vec{H}_A}{dt} = \sum_{j=1}^n \frac{^id \vec{r}_{j/A}}{dt} \times m_j \frac{^id \vec{r}_j}{dt}+ \sum_{j=1}^n \vec{r}_{j/A} \times m_j \frac{ ^id^2 \vec{r}_j}{dt^2} \tag{8} \]
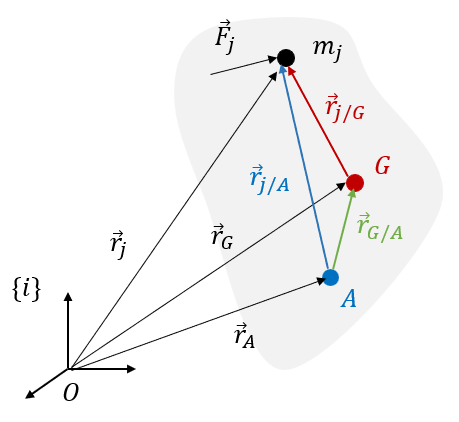
여기서 위 그림에 나와 있듯이 다음과 같은 위치벡터 간의 관계식을 이용하면,
\[ \vec{r}_{j/A}= \vec{r}_{G/A}+ \vec{r}_{j/G} \ , \ \ \ \ \ \vec{r}_j= \vec{r}_G+ \vec{r}_{j/G} \tag{9} \]
식 (8)은 다음과 같이 된다.
\[ \begin{align} \frac{^i d \vec{H}_A}{dt} &= \sum_{j=1}^n \left( \frac{^id \vec{r}_{G/A}}{dt} + \frac{^id \vec{r}_{j/G}}{dt} \right) \times m_j \left( \frac{^i d\vec{r}_G }{dt} + \frac{^id \vec{r}_{j/G}}{dt} \right) + \sum_{j=1}^n \vec{r}_{j/A} \times \vec{F}_j \tag{10} \\ \\ &=m \frac{^id \vec{r}_{G/A}}{dt} \times \vec{v}_G+ \sum_{j=1}^n \vec{M}_{jA} \end{align} \]
여기서 질량중심의 정의 \(\sum_{j=1}^n m_j \vec{r}_{j /G}=0\) 을 이용했으며, \(\vec{v}_G\) 는 질량중심의 속도로서 \(\vec{v}_G=\frac{^i d\vec{r}_G}{dt}\), \(m\) 은 총 질량으로서 \(m=\sum_{j=1}^n m_j\) 이고, \(\vec{M}_{jA}\) 는 점 \(A\) 에 대한 외력 \(\vec{F}_j\) 에 의한 모멘트이다.
만약 점 \(A\) 가 질량중심이라면 식 (10)에서 \( \vec{r}_{G/A}=0\) 이므로 다음 식이 성립한다.
\[ \frac{^id \vec{H}_G}{dt} = \sum_{j=1}^n \vec{M}_{jG} \tag{11} \]
또한 식 (4)에 의하면 위 식은 다음과 같다.
\[ \frac{^id \vec{H}_G^\prime}{dt} = \sum_{j=1}^n \vec{M}_{jG} \tag{12} \]
한편 점 \(A\) 가 관성좌표계의 원점 \(O\) 라면 식 (10)에서 \(\vec{r}_{G/A} = \vec{r}_G\) 이므로 \( \frac{^id \vec{r}_{G/A}}{dt} \times \vec{v}_G= \vec{v}_G \times \vec{v}_G=0\) 이 되어서 다음 식이 성립한다.
\[ \frac{^id \vec{H}_O}{dt} = \sum_{j=1}^n \vec{M}_{jO} \tag{13} \]
따라서 관성좌표계에서 고정된 점 \(O\) 또는 움직이는 질량중심점 \(G\) 에 대한 총 각운동량의 변화율은 점 \(O\) 또는 \(G\)에 관한 외력에 의한 모멘트와 같다는 것을 알 수 있다. 이와 같이 질량중심점에 관해서 모멘트 식을 전개하면 고정된 점에 관해서 식을 전개한 것처럼 식이 간단해진다.
파티클 시스템의 총 운동에너지는 각 파티클이 갖는 운동에너지의 합과 같다.
\[ T=\frac{1}{2} \sum_{j=1}^n m_j \frac{^id \vec{r}_j}{dt} \cdot \frac{^id \vec{r}_j}{dt} \tag{14} \]
식 (9)를 이용하면 위 식을 다음과 같이 전개할 수 있다.
\[ \begin{align} T &= \frac{1}{2} \sum_{j=1}^n m_j \left( \frac{^i d \vec{r}_G}{dt} + \frac{^id \vec{r}_{j/G}}{dt} \right) \cdot \left( \frac{^i d \vec{r}_G}{dt} + \frac{^id \vec{r}_{j/G}}{dt} \right) \tag{15} \\ \\ &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} \sum_{j=1}^n m_j \frac{^id \vec{r}_{j/G}}{dt} \cdot \frac{^id \vec{r}_{j/G}}{dt} \end{align} \]
식 (15)에 의하면, 파티클 시스템의 운동에너지는 질량중심에 집중된 시스템의 전체 질량을 고려하여 얻은 운동에너지에 질량중심에 대한 파티클의 상대적인 운동에너지를 더한 것과 같다.
이로서 강체 운동방정식을 구하기 위한 준비를 모두 마쳤다.
'항공우주 > 동역학' 카테고리의 다른 글
| 강체의 운동방정식 - 4 (0) | 2022.02.07 |
|---|---|
| 강체의 운동방정식 - 3 (0) | 2022.02.06 |
| 강체의 운동방정식 - 1 (0) | 2022.02.03 |
| 해밀톤 방정식 (Hamilton’s Equation) (0) | 2021.08.08 |
| 라그랑지 방정식 (Lagrange’s Equation) (0) | 2021.08.08 |




댓글