해밀톤 방정식 (Hamilton’s Equation)

라그랑지 방정식(Lagrange's equation)은 $n$ 개의 2차 미분 방정식으로 구성되어 있다. 이 방정식을 $2n$ 개의 1차 미분 방정식으로 재 구성한 것이 해밀톤 방정식(Hamilton's equation)이다.

 

 

먼저 일반화된 운동량(generalized momentum)을 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(1)}& p_i=\frac{\partial L}{\partial \dot{q_i}},i=1,2,...,n\end{array}$$

 

이어서 해밀토니안 함수(Hamiltonian function)를 다음과 같이 정의하고,

 

$$\begin{array}{}\text{(2)}& H=\sum _{i=1}^n{p}_i{\dot{q}}_i-L(\mathbf{q},\dot{\mathbf{q}},t)\end{array}$$

 

일반화된 속도 ${\dot{q}}_i$ 대신에 일반화된 운동량 $p_i$ 로 치환하면 해밀토니안은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(3)}& H& =H(q_1,q_2,...,q_n,p_1,p_2,...,p_n,t)\\ & =H(\mathbf{q},\mathbf{p},t)\end{array}$$

 

여기서 $\mathbf{q}=[q_1{q}_2...q_n{]}^T$ 와 $\mathbf{p}=[p_1{p}_2...p_n{]}^T$ 는 각각 $n$ 차원 벡터이다.

식 (3)으로 주어지는 해밀토니안의 변분(variation)을 구하면 다음과 같다.

 

$$\begin{array}{}\text{(4)}& \delta H=\sum _{i=1}^n(\frac{\partial H}{\partial q_i}\delta q_i+\frac{\partial H}{\partial p_i}\delta p_i)\end{array}$$

 

한편 식 (2)로 주어지는 해밀토니안의 변분을 구하면 다음과 같다.

 

$$\begin{array}{r}\text{(5)}& \delta H& =\sum _{i=1}^n(p_i\delta {\dot{q}}_i+{\dot{q}}_i\delta p_i-\frac{\partial L}{\partial q_i}\delta q_i-\frac{\partial L}{\partial {\dot{q}}_i}\delta {\dot{q}}_i)\\ & =\sum _{i=1}^n({\dot{q}}_i\delta p_i-\frac{\partial L}{\partial q_i}\delta q_i)\end{array}$$

 

여기서 식 (1)이 사용되었다.

이제 식(4)와 (5)를 비교하면 다음 식을 얻을 수 있다.

 

$$\begin{array}{r}\text{(6)}& & {\dot{q}}_i=\frac{\partial H}{\partial p_i}\\ & \frac{\partial L}{\partial q_i}=-\frac{\partial H}{\partial q_i},i=1,...,n\end{array}$$

 

만약 홀로노믹 보존(holonomic conservative) 시스템이라면 라그랑지 방정식에 의해서,

 

$$\begin{array}{}\text{(7)}& \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}=0,i=1,...,n\end{array}$$

 

이므로 식 (6)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(8)}& & {\dot{q}}_i=\frac{\partial H}{\partial p_i}\\ & {\dot{p}}_i=-\frac{\partial H}{\partial q_i},i=1,...,n\end{array}$$

 

위 식은 $2n$ 개의 1차 미분 방정식으로서 해밀톤 표준 방정식(Hamilton canonical equation)이라고 한다.

식 (8)의 두 식을 보면 $q_i$ 와 $p_i$ 가 서로 대칭성을 보이는 것을 알 수 있다. 따라서 $q_i$ 와 $p_i$ 를 동일하게 '상태'로 간주하고 둘을 $2n$ 차원 위상벡터(phase vector)로 본다. 그러면 시스템의 운동을 $2n$ 차원 위상공간(phase space)에서의 경로로 나타낼 수 있다.

 

 

 

 

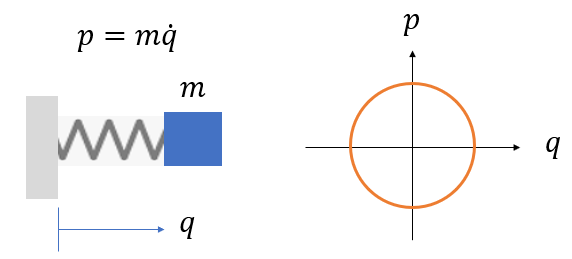
만약 홀로노믹 비보존 시스템이라면 라그랑지 방정식에 의해서,

 

$$\begin{array}{}\text{(9)}& \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}=Q_i,i=1,...,n\end{array}$$

 

이므로 식 (6)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(10)}& & {\dot{q}}_i=\frac{\partial H}{\partial p_i}\\ & {\dot{p}}_i=-\frac{\partial H}{\partial q_i}+Q_i,i=1,...,n\end{array}$$

 

위 식은 홀로노믹 비보존 시스템에 적용되는 해밀톤 방정식이다.

만약 시스템이 $m$ 개의 비홀로노믹 제약조건을 갖는다면,

 

$$\begin{array}{}\text{(11)}& \sum _{i=1}^n{a}_{li}d{q}_i+a_{l0}dt=0,l=1,2,...,m\end{array}$$

 

라그랑지 방정식은 다음과 같으므로

 

$$\begin{array}{}\text{(12)}& \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i}=Q_i+\sum _{l=1}^m{\lambda }_l{a}_{li},i=1,...,n\end{array}$$

 

식 (6)은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(13)}& & {\dot{q}}_i=\frac{\partial H}{\partial p_i}\\ & {\dot{p}}_i=-\frac{\partial H}{\partial q_i}+Q_i+\sum _{l=1}^m{\lambda }_l{a}_{li},i=1,...,n\end{array}$$

 

위 식은 비홀로노믹 시스템에 적용되는 해밀톤 방정식이다.

 

 

한편 식 (3)을 시간 미분하면 다음과 같다.

 

$$\begin{array}{}\text{(14)}& \frac{dH}{dt}=\sum _{i=1}^n(\frac{\partial H}{\partial q_i}{\dot{q}}_i+\frac{\partial H}{\partial p_i}{\dot{p}}_i)+\frac{\partial H}{\partial t}\end{array}$$

 

시스템이 홀로노믹 보존 시스템이라면 식 (8)에 의해서 위 식은 다음과 같이 된다.

 

$$\begin{array}{}\text{(15)}& \frac{dH}{dt}=\frac{\partial H}{\partial t}\end{array}$$

 

따라서 해밀토니안 함수가 명시적인 시간 함수가 아니라면,

 

$$\begin{array}{}\text{(16)}& \frac{dH}{dt}=0\end{array}$$

 

가 된다. 정리하면 홀로노믹 보존 시스템에서 해밀토니안 함수가 명시적인 시간함수가 아니라면 해밀토니안은 보존된다.

덧붙여 만약 홀로노믹 구속조건이 시간의 함수가 아니라면 운동 에너지가 다음과 같이 일반화 속도의 2차 함수로 표현되므로

 

$$\begin{array}{}\text{(17)}& T=\frac{1}{2}\sum _{k=1}^N{m}_k(\sum _{i=1}^n\sum _{j=1}^n\frac{\partial {\mathbf{r}}_k}{\partial q_i}\cdot \frac{\partial {\mathbf{r}}_k}{\partial q_j}{\dot{q}}_i{\dot{q}}_j)\end{array}$$

 

해밀토니안의 정의인 식 (2)에 의하면

 

$$\begin{array}{r}\text{(18)}& H& =\sum _{i=1}^n\frac{\partial L}{\partial {\dot{q}}_i}{\dot{q}}_i-L\\ & =2T-(T-V)\\ \\ & =T+V\end{array}$$

 

홀로노믹 보존 시스템에서 해밀토니안은 기계적인 에너지와 같으므로 해밀토니안 함수가 명시적인 시간함수가 아니라면 기계적인 에너지가 보존된다는 것을 알 수 있다.