지금까지 파티클 시스템(systems of particles)에 대해서 다음과 같은 운동방정식을 얻었다.
\[ \begin{align} & \sum_{j=1}^n \vec{F}_j =m \frac{^id^2 \vec{r}_G }{dt^2}= m \frac{^id \vec{v}_G }{dt} \tag{1} \\ \\ & \sum_{j=1}^n \vec{M}_{jG} = \frac{^id \vec{H}_G }{dt} \tag{2} \\ \\ & \vec{H}_G= \sum_{j=1}^n \vec{r}_{j/G} \times m_j \frac{^id \vec{r}_j}{dt} \\ \\ & T= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G + \frac{1}{2} \sum_{j=1}^n m_j \frac{^id \vec{r}_{j/G}}{dt} \cdot \frac{^i d\vec{r}_{j/G}}{dt} \tag{3} \end{align} \]
여기서 \(G\) 는 질량중심점이다.
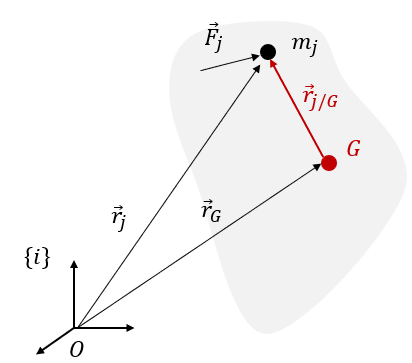
강체(rigid body)를 파티클의 연속적인 집합이며 파티클 사이의 거리가 변하지 않는 파티클 시스템으로 보면 식 (1)~(3)을 합(sum) 기호 대신 적분 기호로 바꾸어 강체에 적용할 수 있다.
다음 그림과 같이 강체를 구성하는 미소(infinitesimal) 질점 dm에 작용하는 미소 외력을 \(d \vec{F}\) 라고 하자. 그리고 강체의 질량중심 \(G\) 를 원점으로 하고 강체에 고정된 좌표계를 강체 좌표계 \(\{b\}\) 라고 하자.
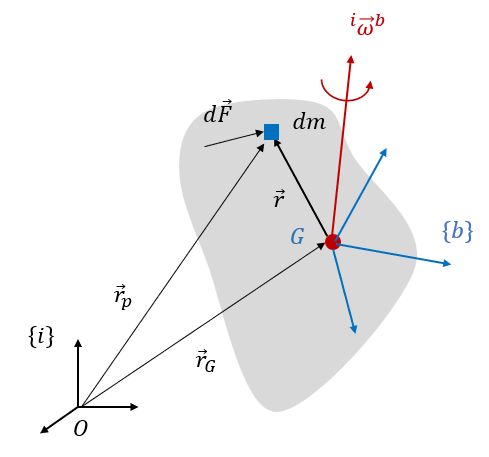
그림에서 \(\vec{r}_G\) 는 관성좌표계 \(\{i\}\) 의 원점에서 질량중심까지의 위치벡터, \(\vec{r}_p\) 는 관성좌표계의 원점에서 미소 질점 \(dm\) 까지의 위치벡터, \(\vec{r}\) 는 강체 좌표계 \(\{b\}\) 의 원점에서 미소 질점 \(dm\) 까지의 위치벡터이다. 그러면 식 (1)로부터 다음 식이 성립한다.
\[ \vec{F}= \int d\vec{F} =m \frac{^id \vec{v}_G }{dt} \tag{4} \]
여기서 \(m\) 은 강체의 질량으로서 \(m= \int dm\) 이다. BKE(Basic Kinematic Equation)을 이용하면 식 (4)를 다음과 같이 전개할 수 있다.
기본 운동학 방정식 (BKE)
동일한 벡터라도 좌표계가 달라지면 그 표현이 달라진다. 뿐만 아니라 동일한 벡터를 시간 미분할 때도 미분을 수행하는 좌표계가 달라지면 그 값이 달라진다. 예를 들어 어떤 원판의 중심에서
pasus.tistory.com
\[ \vec{F}= m \left( \frac{^b d \vec{v}_G}{dt} + ^i \vec{\omega}^b \times \vec{v}_G \right) \tag{5} \]
여기서 \( ^i \vec{\omega}^b\) 는 관성좌표계 \(\{i\}\) 에 대한 강체 좌표계 \(\{b\}\) 의 각속도벡터다. 식 (5)를 병진 운동방정식(translational equation of motion)이라고 한다.
한편, 식 (2)로부터 강체에 작용하는 외력에 의해 생기는 질량중심에 관한 모멘트와 각운동량의 관계식을 얻을 수 있다.
\[ \vec{M}_G = \int d \vec{M}_G = \int \vec{r} \times d \vec{F}= \frac{^id \vec{H}_G }{dt} \tag{6} \]
BKE를 이용하면 식 (6)을 다음과 같이 전개할 수 있다.
\[ \vec{M}_G= \frac{ ^b d \vec{H}_G}{dt} + ^i \vec{\omega}^b \times \vec{H}_G \tag{7} \]
식 (7)에서 강체의 질량중심에 대한 강체의 각운동량 \(\vec{H}_G\) 는 다음과 같이 구할 수 있다.
\[ \begin{align} \vec{H}_G &= \int \vec{r} \times \frac{^i d\vec{r}_p }{dt} dm \tag{8} \\ \\ &= \int \vec{r} \times \left( \frac{^i d \vec{r}_G }{dt} + \frac{^i d \vec{r}}{dt} \right) dm \\ \\ &= \int \vec{r} \times \frac{^i d \vec{r}}{dt} dm \\ \\ &= \vec{H}_{G/G} \end{align} \]
BKE를 사용하여 위 식을 더 전개하면 다음과 같이 된다.
\[ \begin{align} \vec{H}_G &= \int \vec{r} \times \left( \frac{ ^b d \vec{r}}{dt} + ^i \vec{\omega}^b \times \vec{r} \right) dm \tag{9} \\ \\ &= \int \vec{r} \times \left( ^i \vec{\omega}^b \times \vec{r} \right) dm \end{align} \]
강체로 가정했으므로 위 식에서 \( \frac{^b d \vec{r}}{dt}=0\) 이다. 다음과 같은 관계식을 이용하면,
\[ \begin{align} \vec{r} \times \left( ^i \vec{\omega}^b \times \vec{r} \right) &= (\vec{r} \cdot \vec{r} ) ^i \vec{\omega}^b - \vec{r} \left( \vec{r} \cdot ^i \vec{\omega}^b \right) \tag{10} \\ \\ &= \left( \bar{U} r^2 -\vec{r} \ \vec{r} \right) \cdot ^i \vec{\omega}^b \end{align} \]
식 (9)를 다음과 같이 간단하게 표기할 수 있다.
\[ \begin{align} \vec{H}_G &= \int \left( \bar{U} r^2- \vec{r} \ \vec{r} \right) \cdot ^i \vec{\omega}^b dm \tag{11} \\ \\ &= \bar{I}_G \cdot ^i \vec{\omega}^b \end{align} \]
여기서 \(r=| \vec{r} |\) 이며,
\[ \bar{I}_G = \int \left( \bar{U} r^2 - \vec{r} \ \vec{r} \right) dm \tag{12} \]
이다. 식 (10)에서 \(\bar{U}\) 를 단위 다이아딕(unit dyadic)이라고 하며 좌표계 \(\{b\}\) 로 표현하면 다음과 같다.
\[ \bar{U} = \hat{b}_1 \hat{b}_1+ \hat{b}_2 \hat{b}_2+ \hat{b}_3 \hat{b}_3 \tag{13} \]
단위 다이아딕 정의에 의하면 \( \bar{U} \cdot {^i \vec{\omega}^b } = {^i \vec{\omega}^b} \) 가 됨을 알 수 있다.
한편 식 (12)의 \(\bar{I}_G\) 를 점 \(G\) 에 관한 관성 다이아딕(inertia dyadic)이라고 한다. 관성 다이아딕 정의에 의하면 관성 다이아딕은 좌표계의 원점의 위치에 따라서 달라짐을 알 수 있다.
위치벡터 \(\vec{r}\) 의 좌표계 \(\{b\}\) 에 대한 각 축성분을 \(r_j = \vec{r} \cdot \hat{b}_j\) 라 하면 좌표계 \(\{b\}\) 에 관한 관성 다이아딕의 스칼라 성분을 다음과 같이 구할 수 있다.
\[ \begin{align} I_{jk}^b &= \hat{b}_j \cdot \bar{I}_G \cdot \hat{b}_k = \int \hat{b}_j \cdot \left( \bar{U} r^2 -\vec{r} \ \vec{r} \right) \cdot \hat{b}_k \ dm \tag{14} \\ \\ &= \int (r^2 \delta_{jk}- r_j r_k ) dm \end{align} \]
여기서 \(\delta_{jk}\) 는 크로넥커 델타 함수로서 \(j=k\) 일 때는 \(1\) 이고 \(j \ne k\) 이면 \(0\) 이다. 식 (14)를 이용하면 관성 다이아딕을 다음과 같이 좌표계 \(\{b\}\) 로 표현할 수도 있다.
\[ \bar{I}_G = \sum_{j=1}^3 \sum_{k=1}^3 I_{jk}^b \hat{b}_j \hat{b}_k \tag{15} \]
좌표계 \(\{b\}\) 에 관한 관성 다이아딕의 스칼라 성분은 다음과 같이 행렬 형태로 표시할 수 있으며, 이 행렬을 좌표계 \(\{b\}\) 에 관한 관성행렬(inertia matrix) 또는 관성텐서(inertia tensor)라고 한다.
\[ [ I_G^b ] = \begin{bmatrix} I_{11} & I_{12} & I_{13} \\ I_{21} & I_{22} & I_{23} \\ I_{31} & I_{32} & I_{33} \end{bmatrix} \tag{16} \]
관성 다이아딕은 특정 좌표계와 무관하지만 관성 다이아딕을 특정 좌표계로 표현한 관성행렬은 좌표계에 따라 달라짐에 주의해야 한다. 이는 마치 벡터는 좌표계와 무관하지만 벡터를 특정 좌표계로 표현한 ‘벡터(열이 1개인 행렬)’는 좌표계에 따라 달라지는 것과 같다.
식 (11)을 (7)에 대입하면 다음과 같이 된다.
\[ \vec{M}_G ={ \bar{I}_G} \cdot \frac{^b d {^i \vec{\omega}^b} }{dt} + {^i \vec{\omega}^b} \times \left( \bar{I}_G \cdot {^i \vec{\omega}^b} \right) \tag{17} \]
식 (17)을 회전 운동방정식(rotational equation of motion)식이라고 한다. 위 식에 의하면 회전 운동방징식은 병진 운동방정식과 완전히 분리되어 있음을 알 수 있다.
이제, 식 (3)을 이용하여 강체의 운동에너지를 구해보자. 식 (3)을 강체에 적용하면,
\[ T= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} \int \frac{^i d \vec{r}}{dt} \cdot \frac{^i d \vec{r}}{dt} dm \tag{18} \]
BKE를 사용하여 위 식을 더 전개하면 다음과 같이 된다.
\[ \begin{align} T &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} \int \left( \frac{^b d \vec{r}}{dt} + {^i \vec{\omega}^b} \times \vec{r} \right) \cdot \left( \frac{^b d \vec{r}}{dt} + {^i \vec{\omega}^b} \times \vec{r} \right) dm \tag{19} \\ \\ &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} \int \left( {^i \vec{\omega}^b} \times \vec{r} \right) \cdot \left( {^i \vec{\omega}^b} \times \vec{r} \right) dm \\ \\ &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} \int {^i \vec{\omega}^b} \cdot \vec{r} \times \left( {^i \vec{\omega}^b} \times \vec{r} \right) dm \\ \\ &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} {^i \vec{\omega}^b} \cdot \left( \int \vec{r} \times \left( {^i \vec{\omega}^b} \times \vec{r} \right) dm \right) \end{align} \]
위 식의 두번째 줄에서 세번째 줄로 넘어가는 연산에서는 \(\vec{a} \times \vec{b} \cdot \vec{c}= \vec{a} \cdot \vec{b} \times \vec{c}\) 의 관계식을 이용하였다. 식 (9)와 (11)에 의하면 식 (19)는 다음과 같이 된다.
\[ \begin{align} T &= \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} {^i \vec{\omega}^b} \cdot \vec{H}_G \tag{20} \\ \\ & = \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} {^i \vec{\omega}^b} \cdot \left( \bar{I}_G \cdot {^i \vec{\omega}^b} \right) \end{align} \]
식 (20)에 의하면, 강체의 운동에너지는 질량중심의 병진 운동에너지와 질량중심에 대한 회전 운동에너지의 합으로 표현됨을 알 수 있다.
지금까지 질량중심을 기준으로 강체의 운동방정식을 유도하였다. 정리하면 다음과 같다.
\[ \begin{align} & \vec{F}= m \left( \frac{^b d \vec{v}_G}{dt} + {^i\vec{\omega}^b} \times \vec{v}_G \right) \tag{21} \\ \\ & \vec{M}_G = \bar{I}_G \cdot \frac{^b d {^i \vec{\omega}^b} }{dt} + {^i \vec{\omega}^b} \times \left( \bar{I}_G \cdot {^i \vec{\omega}^b} \right) \\ \\ & T = \frac{1}{2} m \vec{v}_G \cdot \vec{v}_G+ \frac{1}{2} {^i \vec{\omega}^b} \cdot \left( \bar{I}_G \cdot {^i \vec{\omega}^b} \right) \end{align} \]
'항공우주 > 동역학' 카테고리의 다른 글
| 라그랑지 방정식을 이용한 강체 운동방정식 유도 (0) | 2022.02.14 |
|---|---|
| 강체의 운동방정식 - 4 (0) | 2022.02.07 |
| 강체의 운동방정식 - 2 (0) | 2022.02.05 |
| 강체의 운동방정식 - 1 (0) | 2022.02.03 |
| 해밀톤 방정식 (Hamilton’s Equation) (0) | 2021.08.08 |




댓글