고체(solid body)는 많은 수의 파티클 (또는 질점)로 구성되어 있는 파티클 시스템(systems of particles)이라고 볼 수 있다. 그 중에서 파티클 사이의 거리가 변하지 않는 시스템을 강체(rigid body)라고 한다. 파티클 사이의 거리가 시간에 따라서 변하는 시스템은 비강체 또는 유연체(탄성체 또는 비탄성체)라고 한다.
파티클 시스템에 적용되는 기본 원리도 강체에 적용되므로 강체의 운동 방정식을 유도하기 위해서 우선 파티클 시스템의 운동 방정식을 유도해 보기로 한다. 다음과 같이 \(n\) 개의 파티클로 구성된 시스템에서 파티클 \(j\) 에 작용하는 힘에는 외력(external force) \(\vec{F}_j\) 와 내력(internal force) \(\vec{f}_{jk}\) 가 있다. 외력은 시스템 외부에서 가해지는 힘이고 내력은 시스템 내에서 다른 파티클과 반응하는 힘으로서 \(\vec{f}_{jk}\) 는 파티클 \(k\) 가 파티클 \(j\) 에 작용하는 힘이다.
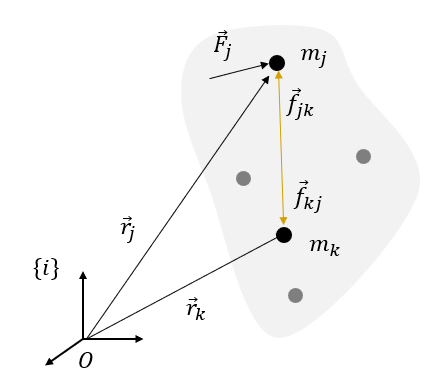
뉴턴의 작용 반작용 법칙에 의하면 파티클 \(k\) 가 파티클 \(j\) 에 작용하는 힘 \(\vec{f}_{jk}\) 와 파티클 \(j\) 가 파티클 \(k\) 에 작용하는 힘 \(\vec{f}_{kj}\) 은 크기가 같고 방향은 서로 반대다.
\[ \ \vec{f}_{jk}= - \vec{f}_{kj} \tag{1} \]
질량이 \(m_j\) 인 파티클 \(j\) 에 뉴턴의 운동 법칙을 적용하면 다음과 같다.
\[ \ \vec{F}_j+ \sum_{k=1}^n \vec{f}_{jk} = m_j \frac{^i d^2 \vec{r}_j}{dt^2} \tag{2} \]
여기서 \(\vec{r}_j\) 는 관성좌표계 \(\{i\}\) 의 원점 \(O\) 에서 파티클 \(j\) 까지의 위치벡터이다. 파티클 시스템을 구성하는 모든 파티클에 대해서 식 (2)가 성립하므로 전체 파티클에 대해서 위 식의 왼쪽항과 오른쪽 항을 모두 더하면 다음과 같다.
\[ \ \sum_{j=1}^n \vec{F}_j + \sum_{j=1}^n \sum_{k=1}^n \vec{f}_{jk} = \sum_{j=1}^n m_j \frac{^i d^2 \vec{r}_j}{dt^2} \tag{3} \]
식 (1)에 의하면 식 (3)은 다음과 같이 된다.
\[ \ \sum_{j=1}^n \vec{F}_j = \sum_{j=1}^n m_j \frac{^i d^2 \vec{r}_j}{dt^2} \tag{4} \]
여기서 시스템의 총 운동량(total linear momentum) \(\vec{L}\) 을 다음과 같이 정의하면,
\[ \ \vec{L}= \sum_{j=1}^n m_j \frac{^i d\vec{r}_j}{dt} = \sum_{j=1}^n m_j \vec{v}_j \tag{5} \]
식 (4)는 다음과 같이 된다.
\[ \ \sum_{j=1}^n \vec{F}_j = \frac{^id \vec{L}}{dt} \tag{6} \]
식 (6)에 의하면 파티클 시스템에 작용하는 외력의 총합과 시스템의 총 운동량의 변화율은 같다. 내력은 시스템의 총 운동량의 변화에 아무 영향을 미치지 못한다.
한편, 관성좌표계의 원점 \(O\) 에 대한 시스템의 총 각운동량(total angular momentum) \(\vec{H}_O\) 를 다음과 같이 정의한다.
\[ \ \vec{H}_O= \sum_{j=1}^n \vec{r}_j \times m_j \vec{v}_j \tag{7} \]
시스템의 총 각운동량과 시스템에 가해지는 모멘트와의 관계식을 알아보기 위해서 식 (2)의 양변에 \(\vec{r}_j\) 를 곱(외적)해 보자.
\[ \ \vec{r}_j \times \vec{F}_j+ \vec{r}_j \times \sum_{k=1}^n \vec{f}_{jk} = \vec{r}_j \times m_j \frac{^i d^2 \vec{r}_j}{dt^2} \tag{8} \]
시스템의 모든 파티클에 대해서 위 식을 모두 더하면 다음과 같이 된다.
\[ \ \sum_{j=1}^n \vec{r}_j \times \vec{F}_j+ \sum_{j=1}^n \vec{r}_j \times \left( \sum_{k=1}^n \vec{f}_{jk} \right) = \sum_{j=1}^n \vec{r}_j \times m_j \frac{^i d^2 \vec{r}_j}{dt^2} \tag{9} \]
파티클 \(j\) 와 \(k\) 에서 두 파티클에 상호 작용하는 내력에 의한 모멘트의 합을 구해보면,
\[ \ \vec{r}_j \times \vec{f}_{jk} + \vec{r}_k \times \vec{f}_{kj}= \vec{r}_j \times (\vec{f}_{jk}+\vec{f}_{kj} )+(\vec{r}_k-\vec{r}_j ) \times \vec{f}_{kj}=0 \tag{10} \]
이 된다. 위 식의 첫번쨰 항은 식 (1)에 의해서 \(0\) 이 되며, 두번째 항은 \((\vec{r}_k-\vec{r}_j )\) 와 \(\vec{f}_{kj}\) 가 서로 평행하기 때문에 \(0\) 이된다. 식 (10)에 의하면 식 (9)의 왼쪽항의 두번째 항은 다음과 같이 \(0\) 이 됨을 알 수 있다.
\[ \ \sum_{j=1}^n \vec{r}_j \times \left( \sum_{k=1}^n \vec{f}_{jk} \right) = \sum_{j=1}^n \sum_{k=1}^n \vec{r}_j \times \vec{f}_{jk} =0 \tag{11} \]
따라서 식 (9)는 다음과 같이 된다.
\[ \ \sum_{j=1}^n \vec{r}_j \times \vec{F}_j = \sum_{j=1}^n \vec{r}_j \times m_j \frac{^id^2 \vec{r}_j}{dt^2} \tag{12} \]
한편 시스템의 총 각운동량 식 (7)을 미분하면 다음과 같다.
\[ \begin{align} \frac{^i d\vec{H}_O}{dt} &= \sum_{j=1}^n \vec{v}_j \times m_j \vec{v}_j + \sum_{j=1}^n \vec{r}_j \times m_j \frac{^i d\vec{v}_j}{dt} \tag{13} \\ \\ &= \sum_{j=1}^n \vec{r}_j \times m_j \frac{^id^2 \vec{r}_j}{dt^2} \end{align} \]
식 (13)과 (12)에 의하면 다음과 같은 식을 얻을 수 있다.
\[ \sum_{j=1}^n \vec{r}_j \times \vec{F}_j = \sum_{j=1}^n \vec{M}_{jO} = \frac{^id \vec{H}_O}{dt} \tag{14} \]
여기서 \(\vec{M}_{jO}\) 는 파티클 \(j\) 에 가해지는 점 \(O\) 에 대한 모멘트(moment)이다. 식 (14)에 의하면 점 \(O\) 에 대해서 파티클 시스템에 작용하는 외력에 의한 모멘트의 총합과 시스템의 총 각운동량의 변화율은 같다. 내력에 의한 모멘트는 시스템의 총 각운동량의 변화에 아무 영향을 미치지 못한다.
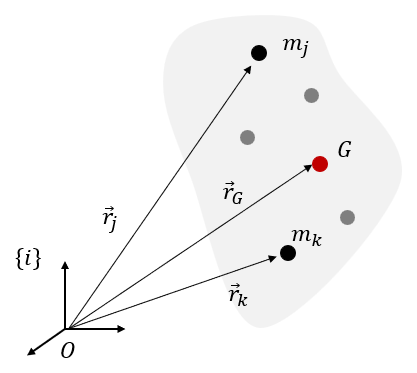
시스템의 질량중심(mass center)은 다음 관계식을 만족하는 위치벡터 \(\vec{r}_G\) 가 가리키는 점 \(G\) 로 정의된다.
\[ m\vec{r}_G = \sum_{j=1}^n m_j \vec{r}_j \tag{15} \]
여기서 \(m\) 은 시스템의 총 질량을 나타내며 \(m=\sum_{j=1}^n m_j\) 이다.
한편, 식 (15)의 양변을 미분하면 다음과 같다.
\[ m \frac{^id \vec{r}_G}{dt} = \sum_{j=1}^n m_j \frac{^i d\vec{r}_j}{dt}= \vec{L} \tag{16} \]
식 (6)과 (16)에 의하면 다음 식이 성립한다.
\[ m \frac{^id^2 \vec{r}_G}{dt^2}= \frac{^id \vec{L}}{dt} = \sum_{j=1}^n \vec{F}_j \tag{17} \]
식 (17)에서 주의할 점은 식 (16)을 미분할 때 시스템의 총 질량이 일정하다는 가정을 사용했다는 점이다. 따라서 시스템의 총 질량이 변화한다면 식 (17)은 성립하지 않는다.
식 (17)에 의하면 파티클 시스템의 질량중심은 시스템의 전체 질량과 모든 외부 힘이 그 지점에 집중된 것처럼 움직인다. 따라서 식 (17)을 수퍼 파티클 정리(super particle theorem)라고도 한다.
또한 식 (17)에 의하면 내력은 질량중심의 운동에 영향을 미치지 않는다는 것을 알 수 있다. 예를 들면 폭발물의 질량중심점은 폭발 후에도 폭발 전의 원래 궤적을 따라 이동한다.
'항공우주 > 동역학' 카테고리의 다른 글
| 강체의 운동방정식 - 3 (0) | 2022.02.06 |
|---|---|
| 강체의 운동방정식 - 2 (0) | 2022.02.05 |
| 해밀톤 방정식 (Hamilton’s Equation) (0) | 2021.08.08 |
| 라그랑지 방정식 (Lagrange’s Equation) (0) | 2021.08.08 |
| 일반화 좌표 (Generalized Coordinate) (0) | 2021.08.08 |




댓글