미사일 운동 방정식을 세우기 위해서는 상황에 따라 다음과 같이 여러 개의 좌표계가 필요하다.
(1) ECI (earth-centered inertial)와 ECEF (earth-centered earth-fixed) 좌표계:
ECI 좌표계
이며 지구자전 각속도

(2) LLH (Latitude-Longitude-Height) 좌표계:
LLH 좌표계 위도, 경도, 높이로 위치를 표시하는 좌표계로서 지리 좌표계(geodetic frame)라고도 한다. 다음 그림에서

LLH 좌표계는 직교 좌표계가 아니기 때문에 DCM(방향코사인행렬) 관계식으로는 표현할 수 없다. LLH 좌표계와 ECEF 좌표계로 표현된 위치 관계식은 다음과 같다.
여기서
이다.
(3) 항법 좌표계:
미사일의 질량 중심점을 원점으로 하거나 또는 그 점의 위치를 지표면에 투사한 점을 원점으로 하고, x축을 북쪽, y축을 동쪽, z축을 지구 중력가속도 방향으로 정의하는 좌표계를 항법 좌표계라고 한다. 보통 항법 시스템에서 많이 사용하는 좌표계이기 때문에 항법 좌표계라고도 한다. 기호로는
이 좌표계는 이동 로컬 탄젠트(moving local tangent) 좌표계라고 하기도 하고 NED(North-East-Down) 좌표계라고도 한다.

항법 좌표계는 좌표계의 원점이 어디에 위치 하느냐에 따라 좌표계의 축 방향이 달라지는 국지적(local) 좌표계이다. ECEF 좌표계에서 NED 좌표계로의 DCM은 다음과 같다.
ECEF 좌표계에서 NED 좌표계의 각속도 식은 다음과 같다.
미사일의 운동 반경이 작다면 NED 좌표계의 원점을 지표면에 고정시키는 경우도 있다. 지표면에 고정되어 있다면 지구와 함께 자전한다는 점에서 ECEF 좌표계와 같다. 원점이 고정되어 있다면 ECEF 좌표계에 대한 NED 좌표계의 각속도 벡터는
방향코사인행렬 (DCM)
DCM은 Direction Cosine Matrix의 약자다. 방향코사인행렬 또는 회전행렬(rotation matrix)이라고 한다. 기호로는
pasus.tistory.com
(4) 미사일 운동 좌표계:
미사일의 질량 중심점을 원점으로 하고 속도 방향을 x축, 지표면과 수평인 평면에서 오른쪽 방향을 y축으로 하는 좌표계를 미사일 운동 좌표계라고 하며, 기호로

NED 좌표계에서 미사일 운동 좌표계로의 DCM은 다음과 같다.
여기서
(5) 미사일 좌표계:
미사일 운동 좌표계의
이렇게 하면 미사일의 양력은 미사일 좌표계의
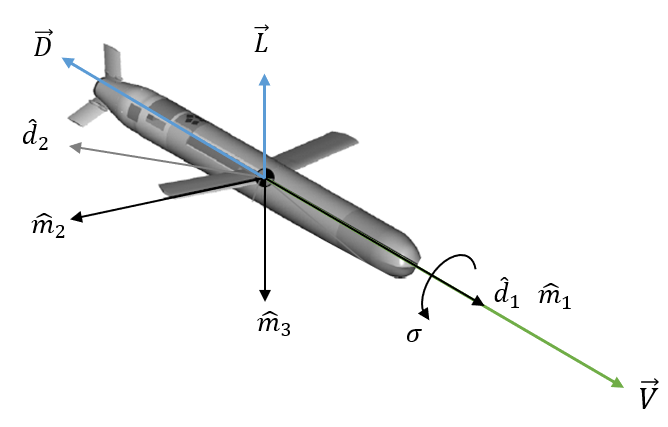
(6) 동체 좌표계:
미사일 좌표계의
미사일을 질점으로 가정하면 동체의 선수 방향이라는 표현은 적당하지 않지만, 추력 벡터가 미사일의 동체 센터 라인과 일치한다고 생각하면 틀린 표현은 아니다. 받음각이 속도벡터와 동체의 센터 라인과의 각도이기 때문에 받음각을 알고 있다면 동체의 선수 방향을 알 수 있다.
여기서 각도
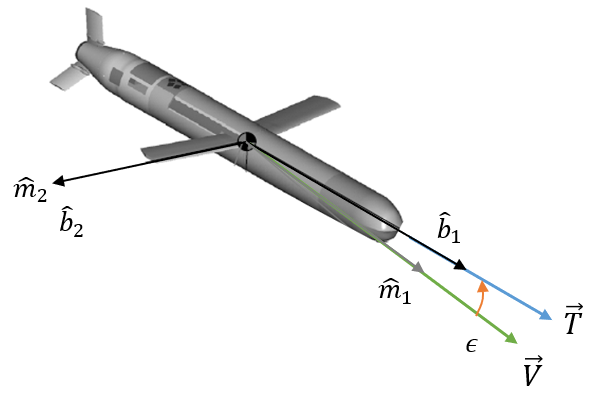
정리하면, 미사일 운동을 위한 좌표계는 관성좌표계부터 시작하여
'항공우주 > 비행역학' 카테고리의 다른 글
| 제트기의 항속시간(Endurance)과 항속거리(Range) (0) | 2022.10.02 |
|---|---|
| NED 좌표계와 LLH 좌표계간의 속도 변환식 (0) | 2022.01.09 |
| 원형 지구 가정에 의한 미사일 운동 방정식 유도 (0) | 2021.12.23 |
| 평평한 지구 가정에 의한 미사일 운동 방정식 유도 (0) | 2021.12.22 |
| ECEF 좌표계에서 미사일 운동 방정식 유도 (0) | 2021.12.21 |




댓글