원형 지구 가정에 의한 미사일 운동 방정식 유도

지구는 자전의 영향으로 약간 타원형이다. 그래서 위도와 경도를 계산하기가 복잡하고, 지면과 수직인 방향이 지구의 중심을 향하지 않기 때문에 수식 전개가 어려워진다. 하지만 지구가 타원형이 아니고 원형이라고 가정하면 이러한 문제가 해결된다.

지구는 이심율이 매우 작은 거의 원형에 가까운 타원형이기 때문에 원형 지구 가정은 지구 재진입 비행체나 중/장거리 미사일의 운동 방정식을 세울 때 많이 사용된다.

 

 

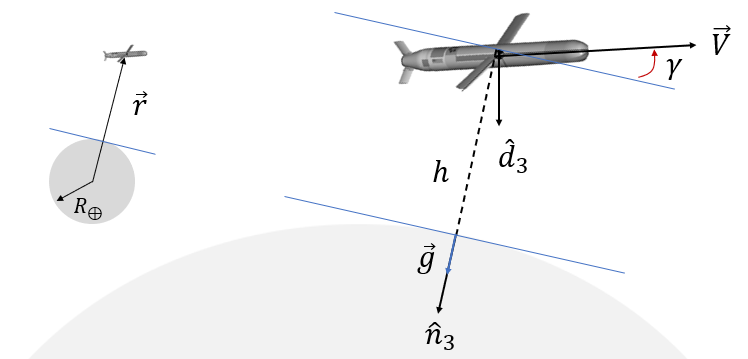
원형 지구 가정에 의해서 다음 식이 성립한다.

 

$$\begin{array}{r}\text{(1)}& & \overrightarrow{r}=-r{\hat{n}}_3\\ & r=R_{mean}+h\\ \\ & \overrightarrow{g}=g{\hat{n}}_3\end{array}$$

 

여기서 $R_{mean}$ 은 지구 평균 반지름이고 $h$ 는 지면에서의 고도, $\{n\}$ 은 이동 NED 좌표계(moving local tangent frame)이다.

ECEF 좌표계에서 미사일의 운동 방정식을 다음과 같이 구한 바 있다(일반적으로 미사일 운동을 위한 좌표계는 $\{i\}\to \{e\}\to \{n\}\to \{d\}\to \{m\}\to \{b\}$ 순으로 전개된다).

 

$$\begin{array}{}\text{(2)}& \frac{{}^{e}d\overrightarrow{V}}{dt}=\frac{\overrightarrow{L}}{m}+\frac{\overrightarrow{D}}{m}+\overrightarrow{g}+\frac{\overrightarrow{T}}{m}-2^i{\overrightarrow{\omega }}^e\times \overrightarrow{V}{-}^i{\overrightarrow{\omega }}^e\times ({}^i{\overrightarrow{\omega }}^e\times \overrightarrow{r})\end{array}$$

 

먼저 속도벡터를 좌표계 $\{d\}$ 에서 미분해 보자. 식 (2)와 BKE를 이용하면 다음 관계식이 성립한다.

 

$$\begin{array}{r}\text{(3)}& \frac{{}^{d}d\overrightarrow{V}}{dt}& =\frac{{}^{e}d\overrightarrow{V}}{dt}{+}^d{\overrightarrow{\omega }}^e\times \overrightarrow{V}\\ & =\frac{\overrightarrow{L}}{m}+\frac{\overrightarrow{D}}{m}+\overrightarrow{g}+\frac{\overrightarrow{T}}{m}\\ \\ & -2^i{\overrightarrow{\omega }}^e\times \overrightarrow{V}{-}^i{\overrightarrow{\omega }}^e\times ({}^i{\overrightarrow{\omega }}^e\times \overrightarrow{r}){+}^d{\overrightarrow{\omega }}^e\times \overrightarrow{V}\end{array}$$

 

방향코사인행렬, 오일러각, 그리고 쿼터니언 | 박성수 | 딥웨이브- 교보ebook

 

식 (3)을 좌표계 $\{d\}$ 로 표현하면 다음과 같다.

 

$$\begin{array}{r}\text{(4)}& {\dot{V}}^d& =-(2[{\omega }_{ie}^d\times ]+[{\omega }_{ed}^d\times ])V^d+\frac{C_m^d{L}^m}{m}+\frac{D^d}{m}\\ & +C_n^d{g}^n+\frac{C_b^d{T}^b}{m}-[{\omega }_{ie}^d\times {]}^2{r}^d\end{array}$$

 

여기서 ${}^d{\overrightarrow{\omega }}^e={-}^e{\overrightarrow{\omega }}^d$ 임을 이용하였다. ${}^e{\overrightarrow{\omega }}^d$ 는 연쇄법칙을 이용하면 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(5)}& {}^e{\overrightarrow{\omega }}^d={}^e{\overrightarrow{\omega }}^n+{}^n{\overrightarrow{\omega }}^d\end{array}$$

 

먼저 ${}^e{\overrightarrow{\omega }}^n$ 을 좌표계 $\{n\}$ 으로 표현하면 다음과 같다.

 

$$\begin{array}{r}\text{(6)}& {\omega }_{en}^n& =C^T(y,-\frac{\pi }{2}-{\lambda }_{lat})(\left[\begin{array}{c}0\\ -{\dot{\lambda }}_{lat}\\ 0\end{array}\right]+C^T(z,{\lambda }_{lon})\left[\begin{array}{c}0\\ 0\\ {\dot{\lambda }}_{lon}\end{array}\right])\\ & =\left[\begin{array}{c}{\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\\ -{\dot{\lambda }}_{lat}\\ -{\dot{\lambda }}_{lon}\sin {\lambda }_{lat}\end{array}\right]\end{array}$$

 

여기서 ${\lambda }_{lon}$ 는 경도, ${\lambda }_{lat}$ 는 위도다.

${}^n{\overrightarrow{\omega }}^d$ 를 좌표계 $\{d\}$ 로 표현하면 다음과 같다.

 

$$\begin{array}{}\text{(7)}& {\omega }_{nd}^d=C_n^d\left[\begin{array}{c}0\\ 0\\ \dot{\psi }\end{array}\right]+\left[\begin{array}{c}0\\ \dot{\gamma }\\ 0\end{array}\right]=\left[\begin{array}{c}-\dot{\psi }\sin \gamma \\ \dot{\gamma }\\ \dot{\psi }\cos \gamma \end{array}\right]\end{array}$$

 

따라서 ${\omega }_{ed}^d$ 는 식 (6)과 (7)을 이용하면 다음과 같이 구할 수 있다.

 

$$\begin{array}{r}\text{(8)}& {\omega }_{ed}^d& =C_n^d{\omega }_{en}^n+{\omega }_{nd}^d\\ & =\left[\begin{array}{c}{\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\cos \psi \cos \gamma -{\dot{\lambda }}_{lat}\sin \psi \cos \gamma +{\dot{\lambda }}_{lon}\sin {\lambda }_{lat}\sin \gamma -\dot{\psi }\sin \gamma \\ -{\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\sin \psi -{\dot{\lambda }}_{lat}\cos \psi +\dot{\gamma }\\ {\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\cos \psi \sin \gamma -{\dot{\lambda }}_{lat}\sin \psi \sin \gamma -{\dot{\lambda }}_{lon}\sin {\lambda }_{lat}\cos \gamma +\dot{\psi }\cos \gamma \end{array}\right]\end{array}$$

 

${\omega }_{ie}^d$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(9)}& {\omega }_{ie}^d& =C_e^d{\omega }_{ie}^e\\ & =\left[\begin{array}{c}{\omega }_{ie}\cos {\lambda }_{lat}\cos \psi \cos \gamma +{\omega }_{ie}\sin {\lambda }_{lat}\sin \gamma \\ -{\omega }_{ie}\cos {\lambda }_{lat}\sin \psi \\ {\omega }_{ie}\cos {\lambda }_{lat}\cos \psi \sin \gamma -{\omega }_{ie}\sin {\lambda }_{lat}\cos \gamma \end{array}\right]\end{array}$$

 

$r^d$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(10)}& r^d=C_n^d{r}^n=\left[\begin{array}{c}r\sin \gamma \\ 0\\ -r\cos \gamma \end{array}\right]\end{array}$$

 

$[{\omega }_{ie}^d\times {]}^2{r}^d$ 는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(11)}& [{\omega }_{ie}^d\times {]}^2{r}^d=\left[\begin{array}{c}r{\omega }_{ie}^2(\cos {\lambda }_{lat}\sin {\lambda }_{lat}\cos \psi \cos \gamma -{\cos }^2{\lambda }_{lat}\sin \gamma )\\ r{\omega }_{ie}^2\cos {\lambda }_{lat}\sin {\lambda }_{lat}\sin \psi \\ r{\omega }_{ie}^2(\cos {\lambda }_{lat}\sin {\lambda }_{lat}\cos \psi \sin \gamma +{\cos }^2{\lambda }_{lat}\cos \gamma )\end{array}\right]\end{array}$$

 

$[{\omega }_{ie}^d\times ]V^d$ 는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(12)}& [{\omega }_{ie}^d\times ]V^d=\left[\begin{array}{c}0\\ V{\omega }_{ie}\cos {\lambda }_{lat}\cos \psi \sin \gamma -V{\omega }_{ie}\sin {\lambda }_{lat}\cos \gamma \\ V{\omega }_{ie}\cos {\lambda }_{lat}\sin \psi \end{array}\right]\end{array}$$

 

$[{\omega }_{ed}^d\times ]V^d$ 는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(13)}& [{\omega }_{ed}^d\times ]V^d=\left[\begin{array}{c}0\\ (V{\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\cos \psi \sin \gamma -V{\dot{\lambda }}_{lat}\sin \psi \sin \gamma \\ -V{\dot{\lambda }}_{lon}\sin {\lambda }_{lat}\cos \gamma +V\dot{\psi }\cos \gamma )\\ V{\dot{\lambda }}_{lon}\cos {\lambda }_{lat}\sin \psi +V{\dot{\lambda }}_{lat}\cos \psi -V\dot{\gamma }\end{array}\right]\end{array}$$

 

$C_m^d{L}^m$ 은 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(14)}& C_m^d{L}^m=\left[\begin{array}{c}0\\ L\sin \sigma \\ -L\cos \sigma \end{array}\right]\end{array}$$

 

$C_n^d{g}^n$ 은 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(15)}& C_n^d{g}^n=\left[\begin{array}{c}-g\sin \gamma \\ 0\\ g\cos \gamma \end{array}\right]\end{array}$$

 

$C_b^d{T}^b$ 는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(16)}& C_b^d{T}^b=\left[\begin{array}{c}T\cos ϵ\\ T\sin \sigma \sin ϵ\\ -T\cos \sigma \sin ϵ\end{array}\right]\end{array}$$

 

 

 

종합하면 식 (4)의 벡터를 각 성분별로 정리하면 다음과 같다.

 

$$\begin{array}{r}\text{(17)}& & \dot{V}=-\frac{D}{m}+\frac{T\cos ϵ}{m}-g\sin \gamma \\ & +r{\omega }_{ie}^2\cos {\lambda }_{lat}(\cos {\lambda }_{lat}\sin \gamma -\sin {\lambda }_{lat}\cos \psi \cos \gamma )\\ \\ \\ & \dot{\psi }=\frac{(L+T\sin ϵ)\sin \sigma }{mV\cos \gamma }+\frac{V\tan {\lambda }_{lat}\sin \psi \cos \gamma }{r}\\ \\ & -2{\omega }_{ie}(\cos {\lambda }_{lat}\cos \psi \tan \gamma -\sin {\lambda }_{lat})\\ \\ & +\frac{r{\omega }_{ie}^2\cos {\lambda }_{lat}\sin {\lambda }_{lat}\sin \psi }{V\cos \gamma }\\ \\ \\ & \dot{\gamma }=\frac{(L+T\sin ϵ)\cos \sigma }{mV}-\frac{g\cos \gamma }{V}\\ \\ & +\frac{V\cos \gamma }{r}+2{\omega }_{ie}\cos {\lambda }_{lat}\sin \psi \\ \\ & +\frac{r{\omega }_{ie}^2}{V}\cos {\lambda }_{lat}(\sin {\lambda }_{lat}\cos \psi \sin \gamma +\cos {\lambda }_{lat}\cos \gamma )\end{array}$$

 

빨간색 부분은 ‘평평한 지구 가정’에 의해 유도된 식에서 추가된 항이다.

한편, 미사일의 위치를 계산하기 위하여 속도 관계식을 살펴보자. 속도 $\overrightarrow{V}$ 는 지면에서의 상대 속도이므로

 

$$\begin{array}{}\text{(18)}& \overrightarrow{V}=\frac{{}^{e}d\overrightarrow{r}}{dt}=\frac{{}^{n}d\overrightarrow{r}}{dt}+{}^e{\overrightarrow{\omega }}^n\times \overrightarrow{r}\end{array}$$

 

이다. 속도벡터를 좌표계 $\{n\}$ 으로 표현하면 다음 식이 성립한다.

 

$$\begin{array}{}\text{(19)}& V^n=C_d^n{V}^d={\dot{r}}^n+[{\omega }_{en}^n\times ]r^n\end{array}$$

 

식 (19)를 풀어 쓰면 다음과 같다.

 

$$\begin{array}{r}\text{(20)}& & {\dot{\lambda }}_{lat}=\frac{V\cos \psi \cos \gamma }{r}\\ & {\dot{\lambda }}_{lon}=\frac{V\sin \psi \cos \gamma }{r\cos {\lambda }_{lat}}\\ \\ & \dot{r}=V\sin \gamma \end{array}$$