이체문제 가정하에서 다음과 같이 기본 궤도 미분 방정식을 유도한 바 있다.
\[ \frac{^i d^2 \vec{r}}{ dt^2} + \frac{\mu}{r^3} \vec{r} =0 \]
여기서 \(\mu=GM\)은 중력 파라미터, \(\vec{r}\)은 관성 좌표계 \(\{i\}\)의 원점에서 질점 \(m\)까지의 위치 벡터, \(r\)은 위치 벡터의 크기, 즉 거리다.

위 식으로 어떤 것을 알 수 있을까.
만유인력은 보존력(conservative force)이므로 만유인력 이외의 다른 힘이 존재하지 않는다는 가정 하에서 질점 \(m\)의 기계적인 에너지(mechanical energy)는 보존될 것으로 예상할 수 있다. 궤도 미분 방정식을 이용하여 질점 \(m\)의 운동 궤도상에서 실제로 기계적인 에너지가 보존되는지를 증명해 보도록 하자.
우선 방정식의 양변과 속도 벡터 \(\vec{v}=\frac{^i d\vec{r}}{dt}\)와의 내적(dot product)을 구해보면 다음과 같다.
\[ \frac{^i d \vec{r}}{ dt} \cdot \left( \frac{^i d^2 \vec{r}}{ dt^2} + \frac{\mu}{r^3} \vec{r} \right) =0 \]
위 식의 좌변을 전개하면
\[ \frac{^i d \vec{r}}{ dt} \cdot \frac{^i d^2 \vec{r}}{ dt^2} + \frac{^i d \vec{r}}{ dt} \cdot \frac{\mu}{r^3} \vec{r} =0 \]
또는
\[ \vec{v} \cdot \frac{^i d \vec{v}}{ dt} + \frac{\mu}{r^3} \vec{r} \cdot \frac{^i d \vec{r}}{ dt} =0 \]
이 된다. 위 식은 어떤 벡터와 그 벡터의 미분 간의 내적에 관한 식인데 이 경우 그 벡터의 크기와 그 미분의 곱셈에 관한 식으로 바꿀 수 있다. 즉, 어떤 벡터 \(\vec{a}\)와 그 크기 \(a\)에 대해서
\[ \vec{a} \cdot \vec{a} = a^2 \]
이므로 양변을 시간 미분하면,
\[ 2 \vec{a} \cdot \frac{d\vec{a}}{dt} = 2a \frac{da}{dt} \]
이 성립한다. 이를 이용하여 위 식을 스칼라 식으로 표현하면 다음과 같다.
\[ v \frac{dv}{dt} + \frac{\mu}{r^3} r \frac{dr}{dt} = 0 \]
여기서 \(v\)는 \(\vec{v}\)의 크기, \(r\)은 \(\vec{r}\)의 크기이다. 좌변을 다시 정리하면,
\[ \frac{d}{dt} \left( \frac{v^2}{2} \right) + \frac{d}{dt} \left( - \frac{\mu}{r} \right) = 0 \]
이 되므로 양변을 적분하면 다음과 같다.
\[ \frac{v^2}{2}- \frac{\mu}{r} =E= constant \]
여기서 \(\frac{v^2}{2}\)은 단위질량당 운동에너지(KE, kinetic energy), \(-\frac{\mu}{r}\)는 단위질량당 위치에너지(PE, potential energy)이다. 운동에너지와 위치에너지의 합이 기계적인 에너지 \(E\)이며, 기계적인 에너지는 질점 \(m\)의 운동 궤도상에서 일정하게 보존됨을 알 수 있다.
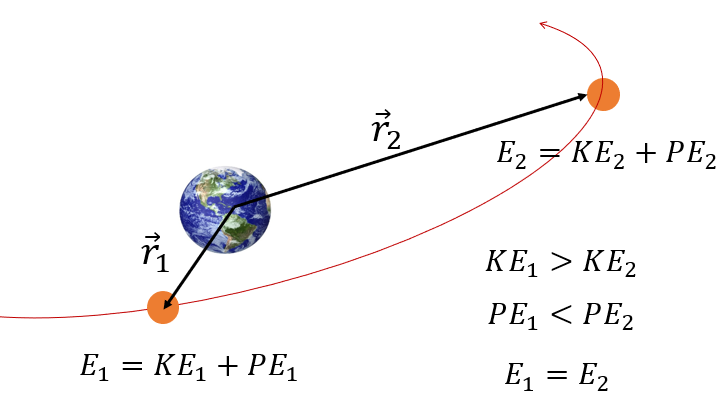
위치에너지는 상대적인 크기를 갖는 에너지이나 여기서는 위치에너지가 \(r=\infty \)에서 \(0\)이 되도록 정의되었으므로 질점 \(m\)의 위치에너지는 항상 음(\(-\))의 값을 갖는다.
에너지 식에 의하면 질점 \(m\)은 질점 \(M\)의 중심에 가까워질수록 (위치에너지가 작아질수록) 속도가 빨라지며 (운동에너지는 커지며), 반대로 질점 \(M\)의 중심에서 멀어질수록 속도는 작아지는 것을 알 수 있다.
'항공우주 > 우주역학' 카테고리의 다른 글
| 삼체문제 (Three-Body Problem) (0) | 2021.04.07 |
|---|---|
| 기본 궤도 미분 방정식 - 궤적 방정식 (0) | 2021.03.01 |
| 기본 궤도 미분 방정식 - 각운동량 보존과 궤도면 (0) | 2021.02.24 |
| 기본 궤도 미분 방정식을 풀기 위한 조건 (0) | 2021.01.12 |
| 더 단순화된 이체문제 (0) | 2021.01.12 |




댓글