기본 궤도 미분 방정식을 풀기 위한 조건

기본 궤도 미분 방정식을 다음과 같이 유도한 바 있다.

 

$$\begin{array}{}\text{(1)}& \frac{{}^i{d}^2\overrightarrow{r}}{d{t}^2}+\frac{\mu }{r^3}\overrightarrow{r}=0\end{array}$$

 

여기서 $\mu =GM$은 중력 파라미터, $\overrightarrow{r}$은 관성 좌표계 $\{i\}$의 원점에서 질점 $m$까지의 위치 벡터, $r$은 위치 벡터의 크기, 즉 거리다.

 

 

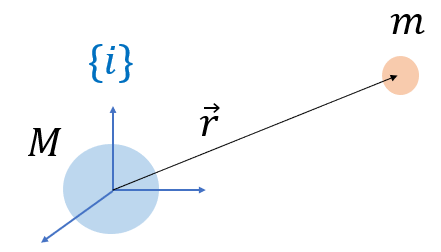
위 식을 유도하는데 다음 3가지 가정을 전제로 했다. 먼저 질량 $m$은 질량 M에 비해서 무시할 수 있을 정도로 작다. 둘째, 질점 $M$은 말 그대로 질점이거나 또는 질점으로 간주할 수 있는 완전한 원구체이며 만유인력은 원구체의 중심을 향한다. 셋째, 질점 $M$과 $m$사이에 작용하는 힘은 만유인력 밖에 없다.

 

 

기본 궤도 방정식은 2차 미분 방정식이기 때문에 식을 풀려면 초기값(initial value)이나 경계값(boundary value)이 필요하다.

초기값을 주고 미분 방정식을 풀어 보라고 하는 문제를 초기값 문제(IVP, initial value problem)라고 한다. 이 경우 초기값은 시간 $t=t_0$에서 주어진 질점 $m$의 위치 및 속도 벡터의 값이다. 초기값을 이용하여 기본 궤도 방정식을 수치 적분하면 질점 $m$의 궤적(위치 및 속도)을 시간의 함수로 나타낼 수 있다.

 

 

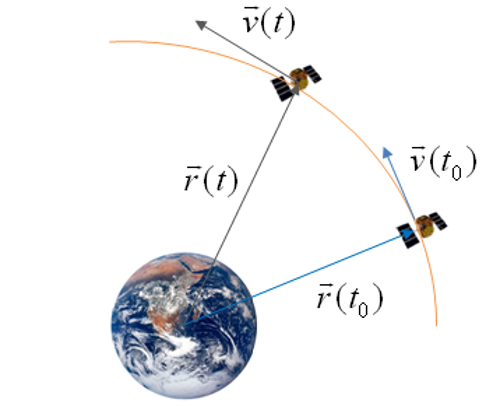
경계값을 주고 미분 방정식을 풀어 보라고 하는 문제를 경계값 문제(BVP, boundary value problem)라고 한다. 이 경우 경계값은 시간 $t=t_0$와 시간 $t=t_f$에서 질점 $m$의 위치 벡터의 값으로 준다. 두 시간 지점에서 값을 주므로 2점 경계값 문제라고도 한다.

한편 이와 같이 2점 경계값을 포함하는 기본 궤도 미분 방정식의 해를 구하는 문제를 램버트 문제(Lambert's problem)이라고 한다. 램버트 문제는 기본적으로 두 개의 위치 벡터와 비행시간 ($t_{tof}=t_f-t_0$ )에 관련된 문제로서 궤도 설계 문제에 많이 사용된다.

초기값 문제와 경계값 문제 중 보통 어느 것이 풀기 쉬울까. 초기값 문제다. 개략적으로 어떻게 푸는지 간단한 예를 통해 살펴보자. 다음과 같이 초기값이 주어진 일차 미분 방정식이 있다고 하자.

 

$$\begin{array}{}\text{(2)}& \dot{x}=5x,x(t_0)=x_0\end{array}$$

 

그러면 가장 쉬운 방법은 시간을 잘게 쪼갠 다음에 미분의 정의를 이용하여 미분 방정식을 근사화하는 것이다.

 

$$\begin{array}{r}\text{(3)}& & \dot{x}(t)\approx \frac{x(t_i)-x(t_{i-1})}{\mathrm{\Delta }t}=5x(t_{i-1})\\ & \to x(t_i)=(1+5\mathrm{\Delta }t)x(t_{i-1})\end{array}$$

 

$\mathrm{\Delta }t=t_i-t_{i-1}$는 잘게 쪼갠 시간의 간격이다. 그리고 주어진 초기값을 이용하여

 

$$\begin{array}{rl}x(t_1)& =(1+5\mathrm{\Delta }t)x(t_0),x(t_0)=x_0\\ \\ x(t_2)& =(1+5\mathrm{\Delta }t)x(t_1)\\ \\ & ⋮\end{array}$$

 

순차적으로 초기 시간부터 $t_0,t_1,t_2,...,$ 마지막 시간까지 시간 전파하면 된다.

경계값 문제의 경우 초기값이 다 주어지지 않았으므로 위 방법대로 시간 전파를 할 수는 없다. 대신 주어지지 않은 초기값, 램버트 문제에서는 초기 속도 벡터를 적당히 추정한 다음에 초기값 문제를 풀 듯이 순차적으로 시간 전파해 본다. 그리고 시간이 $t_f$일 때 경계값으로 주어진 위치 벡터와 비교해 본다. 처음부터 딱 들어맞을 리는 없고 오차가 있을 것이다. 그 오차를 바탕으로 초기 속도 벡터를 다른 값으로 바꿔본다. 그리고 다시 이 값을 초기값 삼아 시간 전파하는 것이다. 몇번하다 보면 시간이 $t_f$일 때 경계값으로 준 위치 벡터와 들어맞는데 이러면 경계값 문제를 푼 것이다. 이와 같은 방법을 슈팅 방법(shooting method)이라고 한다. 슈팅 방법에서는 오차를 바탕으로 초기값을 수정하는 방법도 제공해 준다.

슈팅 방법은 앵그리버드와 같은 슈팅 게임에서 이미 많이 쓰는 방법이다. 앵그리버드에서는 일단 새를 쏴 보고 날아간 거리를 고려해서 다음 번에 새를 쏠 때 방향과 강도를 조정한다.