이체문제 가정하에서 다음과 같이 기본 궤도 미분 방정식을 유도한 바 있다.
\[ \frac{^i d^2 \vec{r}}{ dt^2} + \frac{\mu}{r^3} \vec{r} =0 \]
여기서 \(\mu=GM\)은 중력 파라미터, \(\vec{r}\)은 관성 좌표계 \(\{i\}\)의 원점에서 질점 \(m\)까지의 위치 벡터, \(r\)은 위치 벡터의 크기, 즉 거리다.
위 식으로 알 수 있는 것에는 또 무엇이 있을까.
궤도의 모양을 알 수 있다. 궤도 미분 방정식에 의하면 궤도의 모양은 4가지밖에 없다. 원궤도, 타원궤도, 포물선궤도, 쌍곡선궤도가 그것이다. 어떻게 궤도의 모양을 알 수 있는지 살펴보도록 하자.
사실 궤도 미분 방정식을 풀면 질점 \(m\)의 운동 궤도 모양을 알 수 있다. 위 식은 비선형 미분 방정식이므로 해석적인 방법으로는 풀 수 없으며 수치해석을 통하여 해를 구하는 수밖에 없다. 또한 위 식은 2차 미분 방정식이므로 해를 구하기 위해서는 위치 벡터의 초기값 \(\vec{r} (t_0)\)와 속도 벡터의 초기값 \(\vec{v}(t_0)\) 등 2개의 벡터 초기값이 필요하다.
이 2개의 초기값이 전 시간 범위 \(t \ge t_0\)에서 질점 \(m\)의 운동 특성을 결정짓는 조건이기는 하지만, 수치해석을 통하여 식을 실제로 풀기 전까지는 질점 \(m\)이 어떤 속도로 어떤 모양의 궤도를 그리며 운동할 지는 전혀 알 수가 없다. 하지만 이체문제의 경우 직접 해를 구하지 않고도 초기값과 궤도 모양과의 관계를 도출해 낼 수 있는 방법이 있다.
먼저 기본 방정식의 양변과 각운동량과의 벡터곱(cross product)을 구하기로 한다. 그러면
\[ \vec{h} \times \left( \frac{^i d^2 \vec{r}}{ dt^2} + \frac{\mu}{r^3} \vec{r} \right) =0 \]
이 된다. 위 식을 전개하면
\[ \frac{^i d^2 \vec{r}}{ dt^2} \times \vec{h} = \frac{\mu}{r^3} \left( \vec{h} \times \vec{r} \right) \]
이 된다. \(\vec{h} = \vec{r} \times \vec{v} = constant\) 임을 이용하여 위 식을 정리하면 다음과 같다.
\[ \frac{^i d }{ dt} \left( \frac{^i d \vec{r}}{ dt} \times \vec{h} \right) = \frac{\mu}{r^3} \left[ (\vec{r} \times \vec{v} ) \times \vec{r} \right] \]
여기서 \( (\vec{a} \times \vec{b} ) \times \vec{c} = (\vec{a} \cdot \vec{c} ) \vec{b} -( \vec{a} \cdot \vec{b} ) \vec{c}\) 의 관계를 이용하여 우변을 다시 쓰면,
\[ \begin{align} \frac{^i d }{ dt} \left( \frac{^i d \vec{r}}{ dt} \times \vec{h} \right) &= \frac{\mu}{r^3} \left[ (\vec{r} \cdot \vec{r} ) \vec{v} - ( \vec{r} \cdot \vec{v} ) \vec{r} \right] \\ \\ &= \frac{\mu}{r^3} \left[ r^2 \vec{v} - rv \vec{r} \right] \\ \\ &= \frac{\mu}{r} \vec{v} - \frac{\mu}{r^2} \dot{r} \vec{r} \\ \\ &= \mu \frac{^i d}{dt} \left( \frac{\vec{r}}{r} \right) \end{align} \]
이 된다. 이제, 양변을 적분하면,
\[ \frac{^i d \vec{r}}{ dt} \times \vec{h} = \mu \frac{\vec{r}}{r} + \vec{B} \]
이 된다. \(\vec{B}\)는 적분 상수 벡터이다. 위 식의 양변과 \(\vec{t}\)의 내적(dot product)을 구하면
\[ \vec{r} \cdot \left( \frac{^i d \vec{r}}{ dt} \times \vec{h} \right) = \vec{r} \cdot \left( \mu \frac{\vec{r}}{r} + \vec{B} \right) \]
이 된다. 위 식을 전개하면 다음과 같이 된다.
\[ \left( \vec{r} \times \frac{^i d \vec{r}}{ dt} \right) \cdot \vec{h} = \mu r + rB \cos \theta \]
여기서 \(B\)는 벡터 \(\vec{B}\)의 크기이며 \(\theta\)는 \(\vec{r}\)과 \(\vec{B}\)의 사잇각이다.
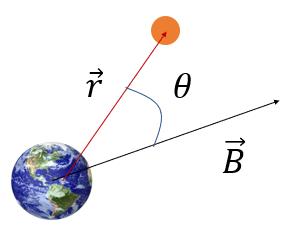
위 식에서 좌변의 괄호는 \(\vec{h}\)이므로 질점 \(M\)의 중심에서 질점 \(m\)까지의 거리 \(r\)로 정리하면
\[ \begin{align} r &= \frac{ h^2 }{ \mu + B \cos\theta } \\ \\ & = \frac{ \frac{h^2}{\mu} }{ 1 + \frac{B}{\mu} \cos\theta } \end{align} \]
이 된다. 여기서 \(\mu, h, B\)는 상수임에 주의하자. \( p= \frac{h^2}{\mu}\)라 하고 \(e= \frac{B}{\mu}\)라 놓으면 위 식은 최종적으로 다음과 같이 된다.
\[ r = \frac{ p }{ 1 + e \cos\theta } \]
여기서 \(p\)와 \(e\)는 상수다. 위 식을 궤적 방정식(trajectory equation)이라고 한다. \(p\)를 통반경 (semi-latus rectum), \(e\)를 이심율 (eccentricity), \(\theta\)는 실제 비행각(true anomaly)이라고 부른다.
아래 그림과 같이 원추를 어떻게 자르느냐에 따라 원추의 단면은 원 (circle), 타원 (ellipse), 포물선 (parabola), 쌍곡선 (hyperbola) 모양이 되는데, 궤적 방정식도 \(e\)값에 따라서 각각 원, 타원, 포물선, 쌍곡선의 식이 된다.
따라서 원추의 단면이 가질 수 있는 모양과 궤적 방정식이 나타낼 수 있는 모양이 일치하기 때문에 궤적 방정식을 원추 단면 방정식 (equation for conic section)이라고도 한다.
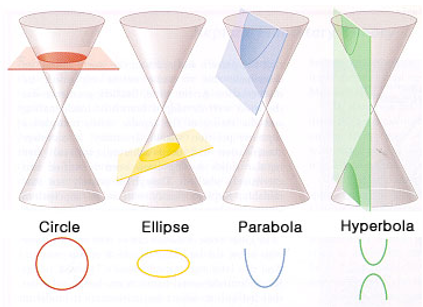
궤적 방정식은 이체문제 가정하에서 질점 \(m\)이 가질 수 있는 궤도의 종류가 원, 타원, 포물선, 쌍곡선 궤도 밖에 없다는 것을 보여주고 있다.
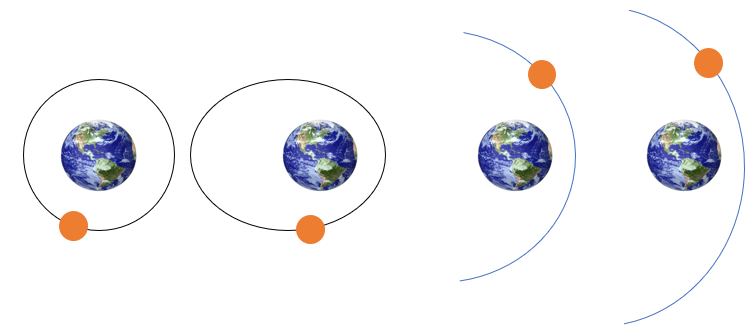
그런데 궤적 방정식에서 원, 타원, 포물선, 쌍곡선의 모양이 보이는가? \(e=0\) 이라면 \(r=p\)가 되므로 원의 방정식이 된다는 것은 쉽게 알 수 있다. 하지만 타원, 포물선, 쌍곡선은?
'항공우주 > 우주역학' 카테고리의 다른 글
| [CR3BP] 운동방정식 유도 (0) | 2021.04.08 |
|---|---|
| 삼체문제 (Three-Body Problem) (0) | 2021.04.07 |
| 기본 궤도 미분 방정식 - 궤도 에너지 보존 (0) | 2021.02.25 |
| 기본 궤도 미분 방정식 - 각운동량 보존과 궤도면 (0) | 2021.02.24 |
| 기본 궤도 미분 방정식을 풀기 위한 조건 (0) | 2021.01.12 |




댓글