이체문제 가정하에서 다음과 같이 기본 궤도 미분 방정식을 유도한 바 있다.
\[ \frac{^i d^2\vec{r}}{dt^2} + \frac{\mu}{r^3} \vec{r} = 0 \]
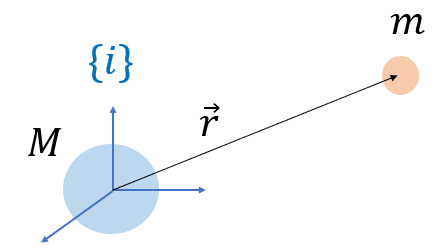
여기서 \(\mu=GM\)은 중력 파라미터, \(\vec{r}\)은 관성 좌표계 \(\{i\}\)의 원점에서 질점 \(m\)까지의 위치 벡터, \(r\)은 위치 벡터의 크기, 즉 거리다.
위 식으로 어떤 것을 알 수 있을까.
먼저 3차원 공간상에 있는 질점 \(m\)은 특정 평면내에서만 운동한다는 것을 알 수 있다. 이 평면을 궤도면(orbital plane)이라고 한다. 질점 \(M\)을 태양, 질점 \(m\)을 지구로 본다면 지구의 공전면을 황도면이라고 하는데, 지구는 태양 주위를 돌지만 황도면을 벗어나지는 못한다. 질점 \(M\)을 지구, 질점 \(m\)을 인공위성으로 본다면 인공위성은 지구 주위를 돌지만 정해진 공전면을 벗어나지는 못한다. 이 사실을 어떻게 알 수 있을까.
질점 \(M\)에 의해 질점 \(m\)에 작용하는 만유인력이 항상 질점 \(M\)의 중심 방향으로만 작용하기 떄문에 질점 \(m\)의 각운동량 (angular momentum)이 보존될 것으로 예상할 수 있다. 궤도 미분 방정식을 이용하여 질점 \(m\)의 운동 궤도상에서 실제로 각운동량이 보존되는지를 증명해 보도록 하자.
우선 방정식의 양변과 위치 벡터와의 벡터곱(cross product)을 계산하기로 한다. 그러면,
\[ \vec{r} \times \left( \frac{^i d^2\vec{r}}{dt^2} + \frac{\mu}{r^3} \vec{r} \right) = \vec{r} \times 0 \]
이 된다. 위 식에서 \(\vec{r} \times \vec{r}=0\) 이므로 좌변을 정리하면,
\[ \vec{r} \times \frac{^i d^2\vec{r}}{dt^2} =\frac{^i d}{dt} \left( \vec{r} \times \frac{^i d\vec{r}}{dt} \right) = 0 \]
이 되며, 속도 벡터는 \(\vec{v}= \frac{^i d\vec{r}}{dt}\)이므로 양변을 적분하면
\[ \vec{r} \times \vec{v} = \vec{h} = constant \]
가 된다. 여기서 단위 질량당 각운동량 벡터인 \(\vec{h}\)가 일정하기 때문에 질점 \(m\)의 모든 궤도상에서 각운동량 벡터가 보존됨을 알 수 있다. 각운동량 벡터는 벡터이므로 크기 뿐만 아니라 방향도 항상 일정하게 유지된다.
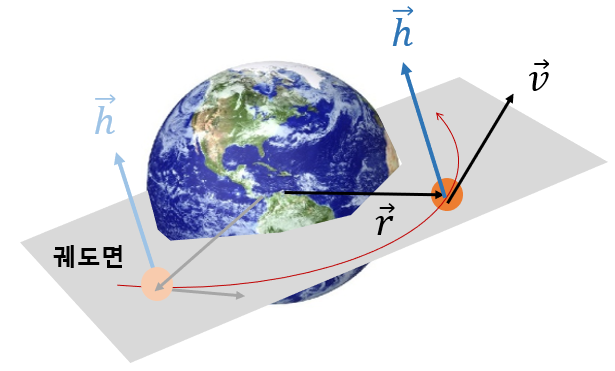
위 식에 의하면, 각운동량 벡터의 방향은 위치 벡터 \(\vec{r}\)과 속도 벡터 \(\vec{v}\)에 각각 직각인 방향이며 그 방향은 항상 일정하다는 아주 중요한 의미를 내포하고 있다. 따라서 위치 벡터와 속도 벡터가 만드는 평면은 각운동량 벡터와 항상 직각이며, 그 평면은 관성좌표계에 대해서 항상 일정하게 유지된다는 것을 알 수 있다.
질점 \(m\)의 위치 벡터와 속도 벡터가 만드는 평면을 '궤도면 (orbital plane)' 이라고 부른다. 궤도면은 각운동량 벡터와 직각이며, 궤도면에는 질점 \(m\)의 위치 벡터와 속도 벡터가 항상 포함돼 있어야 하므로 질점 \(m\)은 궤도면 밖으로 이탈할 수 없고 궤도면 내에서만 운동할 수 있다.
'항공우주 > 우주역학' 카테고리의 다른 글
| 기본 궤도 미분 방정식 - 궤적 방정식 (0) | 2021.03.01 |
|---|---|
| 기본 궤도 미분 방정식 - 궤도 에너지 보존 (0) | 2021.02.25 |
| 기본 궤도 미분 방정식을 풀기 위한 조건 (0) | 2021.01.12 |
| 더 단순화된 이체문제 (0) | 2021.01.12 |
| 기본 궤도 미분 방정식 (0) | 2021.01.11 |




댓글