좌표변환 방법으로서 방향코사인행렬(DCM), 오일러각, 그리고 쿼터니언에 대해서 알아보았다.
이제 각각의 장단점을 비교해 보자.
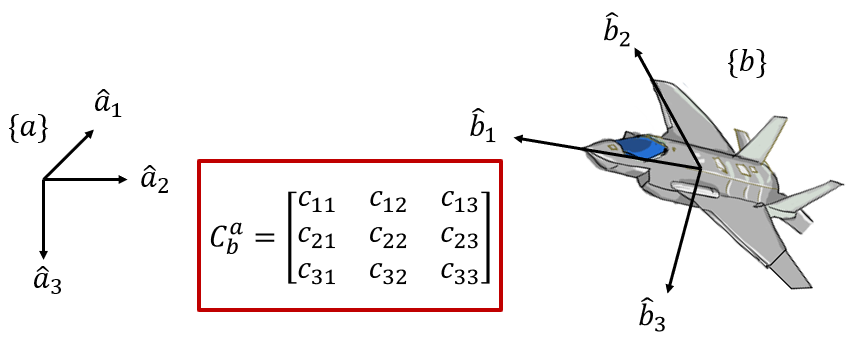
먼저 DCM은 9개의 파라미터로 좌표변환을 표현한다. 그 중 6개는 구속조건을 만족해야 한다. 구속조건은 DCM이 단위직교 행렬(orthonormal matrix)이어야 한다는 것이었다. 이 구속 조건을 맞추기가 쉽지 않다는 것이 DCM의 큰 단점이다.
시간이 흐름에 따라서 좌표계의 자세가 달라질 경우 DCM의 미분 방정식을 세우고 이 방정식을 적분하여 매시간 마다 DCM을 계산해야 하는데, 이 때 수치 오차 때문에 계산된 DCM이 단위직교 행렬이 안될 수가 있다. DCM은 반드시 단위직교 행렬이어야 하므로 강제적으로 단위직교 행렬로 만들어야 할 필요가 있는데, 이것이 쉽지 않다는 뜻이다.
DCM의 또 다른 단점은 직관적이지 않다는 것이다. DCM의 9개 숫자를 보고 두 좌표계의 상대적인 자세를 상상하기란 매우 어렵다. 하지만 DCM은 좌표변환이 쉽고 연쇄법칙이 적용된다는 장점이 있다.

오일러각은 3개의 파라미터로 좌표변환을 표현한다. 최소의 파라미터를 사용하므로 잉여 파라미터가 없기 때문에 달리 구속조건이 없다. 또한 직관적인 좌표변환 방법이다. 오일러각 3개를 주면 두 좌표계의 상대적인 자세가 어떨 것인지 쉽게 상상할 수 있다. 대신 짐벌락 또는 특이점이 존재하는 것이 큰 단점이다. 또한 사인과 코사인 등 삼각함수를 계산해야 하기 때문에 은근히 계산량이 많다는 것도 단점 중의 하나다.
또 다른 단점으로는 연쇄법칙이 적용 안된다는 것이다. 좌표계 \(\{a\}\)에서 \(\{b\}\)로의 오일러각이 \(\phi_1, \theta_1, \psi_1\)이고, 좌표계 \(\{b\}\)에서 \(\{c\}\)로의 오일러각이 \(\phi_2, \theta_2, \psi_2\)라고 할 때, 좌표계 \(\{a\}\)에서 \(\{c\}\)로의 오일러각을 \(\phi_1, \theta_1, \psi_1\)과 \(\phi_2, \theta_2, \psi_2\)를 이용해서 계산하는 방법이 없다는 뜻이다. DCM과 쿼터니언의 경우는 쉬웠다.

쿼터니언은 4개의 파라미터로 좌표변환을 표현한다. 1개의 잉여 파라미터가 있는데 구속조건은 쿼터니언 벡터의 크기가 1이어야 한다는 것이다. 이 조건을 맞추기는 매우 쉽다. 만약 수치 오차 때문에 적분 계산된 쿼터니언 벡터의 크기가 1이 아니더라도 강제로 그 크기를 1로 맞추기는 쉽다. 쿼터니언 벡터의 현재 크기로 나눠주면 그만이다.
단점은 DCM과 마찬가지로 직관적이지 않다는 것이다. 장점은 오일러각 방법과 같은 특이점이 존재하지 않고, DCM 보다도 훨씬 적은 파라미터만으로 좌표변환을 표현할 수 있으며, 연쇄법칙이 적용된다는 것을 들 수 있다.
이와 같이 DCM, 오일러각, 쿼터니언은 각각의 장점과 단점이 있다. 보통은 특이점이 있음에도 불구하고 오일러각이 많이 쓰이지만, 응용 문제에 따라서는 어느 한가지 방법만을 사용하지 않고, 서로 간의 상호 변환 관계식을 이용하여 2가지 또는 3가지 모두 사용하는 경우가 많다.
예를 들면 미분 방정식은 쿼터니언을 이용하여 수치 적분하며, 벡터의 좌표변환은 DCM으로 하고, 두 좌표계 간의 상대적인 자세를 사용자에게 표시할 때는 오일러각을 이용하는 식이다.
'항공우주 > 동역학' 카테고리의 다른 글
| 기본 운동학 방정식 (BKE) (0) | 2021.04.13 |
|---|---|
| 각속도 벡터 (0) | 2021.04.13 |
| 쿼터니언 (Quaternions) (0) | 2021.02.08 |
| 짐벌락 (Gimbal Lock) (0) | 2021.02.07 |
| 오일러각 (Euler Angles) (0) | 2021.02.07 |




댓글