오일러의 회전 정리(Euler's rotation theorem)에 의하면 모든 좌표변환은 어떤 회전축과 그 회전축을 중심으로 하는 한번의 회전을 통해서 가능하다. 쿼터니언(quaternions)의 정의는 이 회전축과 회전각에 기반을 두고 있다.
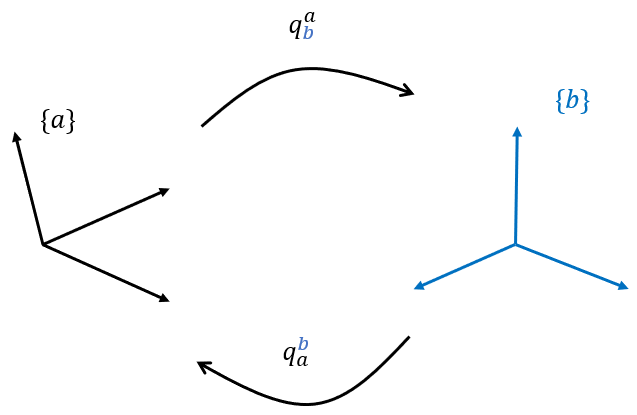
좌표계 \(\{a\}\)를 회전축 \(\hat{p}\) 를 중심으로 회전각 \(\beta\) 만큼 회전하여 좌표계 \(\{b\}\)로 변환했다고 하면, 좌표계 \(\{a\}\)에서 좌표계 \(\{b\}\)로의 쿼터니언 \(q_b^a\)는 다음과 같이 정의된다.
\[ q_b^a= \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{bmatrix} = \begin{bmatrix} \cos \left( \frac{\beta}{2} \right) \\ p_1 \sin \left(\frac{\beta}{2} \right) \\ p_2 \sin \left( \frac{\beta}{2} \right) \\ p_3 \sin \left( \frac{\beta}{2} \right) \end{bmatrix} \]
여기서
\[ \mathbf{p}^a=\mathbf{p}^b= \begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix} \]
이다. 쿼터니언은 정의와 같이 4개의 실수값으로 구성되어 있기 때문에 사원수라고 번역되기도 한다.
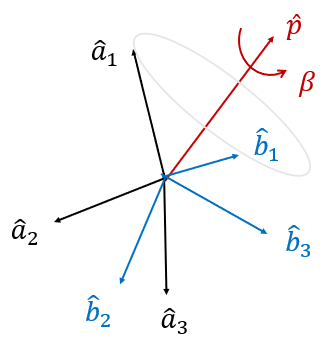
\(q_0\)를 쿼터니언의 스칼라부(scalar part)라고 하며 \( \begin{bmatrix} q_1 & q_2 & q_3 \end{bmatrix}^T\)를 쿼터니언의 벡터부(vector part)라고 한다.
회전축 \(\hat{p}\) 를 중심으로 반대 방향으로 회전각 \(\beta\) 만큼 회전하면 쿼터니언은
\[ q_b^a= \begin{bmatrix} \cos \left( \frac{\beta}{2} \right) \\ -p_1 \sin \left(\frac{\beta}{2} \right) \\ -p_2 \sin \left( \frac{\beta}{2} \right) \\ -p_3 \sin \left( \frac{\beta}{2} \right) \end{bmatrix} \]
가 되어 벡터부만 부호가 바뀐다. 이를 켤레 쿼터니언(quaternions conjugate)이라고 하고 기호로 \( \left( q_b^a \right)^\star\) 로 표시한다.
좌표계 \(\{b\}\)에서 좌표계 \(\{a\}\)로의 쿼터니언은 벡터 \(q\)의 위 첨자와 아래 첨자를 반대로 써서 \(q_a^b\)로 표현할 수 있다. \(q_b^a\)와 \(q_a^b\)는 서로 역변환 관계로서 \(q_a^b=\left( q_b^a \right)^\star\)의 식이 성립한다.
쿼티니언 \(q\)와 \(r\)의 곱셈을 다음과 같이 벡터와 행렬 형식으로 정의할 수 있다. 쿼터니언 곱셈은 \(\otimes\)로 표기한다.
\[ \begin{align} q \otimes r &= \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{bmatrix} \otimes \begin{bmatrix} r_0 \\ r_1 \\ r_2 \\ r_3 \end{bmatrix} \\ \\ &= \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{bmatrix} \begin{bmatrix} r_0 \\ r_1 \\ r_2 \\ r_3 \end{bmatrix} \\ \\ &= \left[ q \right] r \end{align} \]
여기서 \(\left[ q \right]\)을 쿼터니언 행렬이라고 한다.
쿼티니언은 본래 아일랜드의 수학자 해밀턴(William R. Hamilton)이 1843년에 복소수를 확장시켜 만든 수체계(number system)다. 복소수가 2차원 평면상의 점을 표현할 수 있다는 사실로부터 3차원 공간상의 점을 표현하는 방법을 찾다가 만들었다고 한다. 쿼터니언 곱셈도 쿼터니언 수체계의 기본 규칙에서 파생되었다.
쿼터니언의 정의에 의해서 다음 3가지 성질이 파생된다.
먼저, 벡터 \(\vec{u}\)를 좌표계 \(\{a\}\)로 표현한 벡터 \(\mathbf{u}^a\)와 좌표계 \(\{b\}\)로 표현한 \(\mathbf{u}^b\)는 다음 관계가 있다.
\[ \bar{\mathbf{u}}^a = q_b^a \otimes \bar{\mathbf{u}}^b \otimes \left( q_b^a \right)^\star \]
여기서 \(\bar{\mathbf{u}}^a\)는 쿼터니언이 \(4 \times 1\) 벡터임을 감안하여 벡터 \(\mathbf{u}^a\)를 쿼터니언 벡터화한 것으로 다음과 같이 정의한다.
\[ \bar{\mathbf{u}}^a= \begin{bmatrix} 0 \\ \mathbf{u}^a \end{bmatrix} \]
위 식에 의하면 쿼터니언 \(q_b^a\)는 좌표계 \(\{b\}\)에서 표현한 벡터 \(\mathbf{u}^b\)를 좌표계 \(\{a\}\)에서 표현한 벡터 \(\mathbf{u}^a\)로 변환해 준다.
쿼터니언의 두번째 성질은 쿼터니언의 크기가 1이라는 것이다. 즉,
\[ \begin{align} \left( q_b^a \right)^T q_b^a &= \cos^2 \left( \frac{\beta}{2} \right) + \left( \mathbf{p}^a \right)^T \mathbf{p}^a \sin^2 \left( \frac{\beta}{2} \right) \\ \\ &= 1 \end{align} \]
여기서 \(\mathbf{p}^a\)는 회전축 방향을 표시하는 단위 벡터이기 때문에 크기는 1이다.
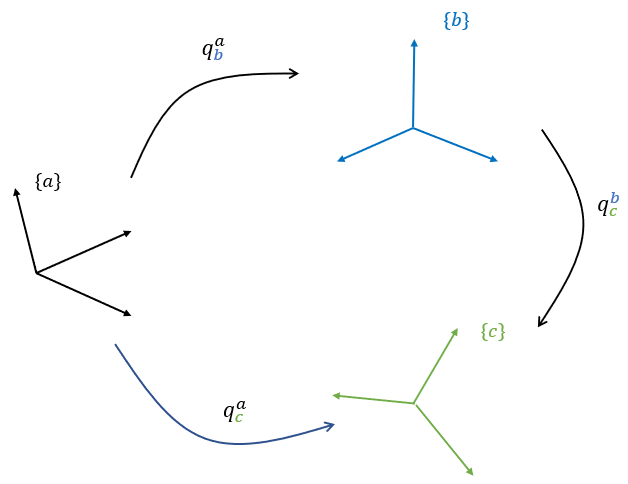
쿼터니언의 세번째 성질은 연쇄법칙이 성립한다는 것이다. 연쇄법칙은 다음과 같은 것이다.
\[ q_c^a=q_b^a \otimes q_c^b \]
좌표계 \(\{a\}\)에서 좌표계 \(\{c\}\)로의 쿼터니언을 직접 계산할 수도 있지만 중간 단계의 좌표계 \(\{b\}\)를 두고 각각의 쿼터니언을 계산해서 구할 수도 있다는 이야기다. 즉 \(\{a\}\)에서 \(\{c\}\)로 가는 것은 \(\{a\}\)에서 \(\{b\}\)로, 다시 \(\{b\}\)에서 \(\{c\}\)로 가는 것과 같다는 뜻이다.
쿼터니언의 첫번째 성질을 증명하려면 좀 복잡한 과정을 거쳐야 하므로 증명은 하지 않겠다. 세번째 성질은 첫번째 성질을 이용하면 쉽게 증명할 수 있다. 쿼터니언에 관한 자세한 사항은 다음 책을 참고하면 좋을 것 같다.
방향코사인행렬, 오일러각, 그리고 쿼터니언
<b>“좌표계간의 상호 변환관계를 말하다”</b> <b>“물체의 자세 변화를 수학적으로 표현하고 싶은 개발자를 위한 책”</b> 이 책은 방향코사인행렬, 오일러각, 쿼터니언과 이들의 시간 변화율에
digital.kyobobook.co.kr
'항공우주 > 동역학' 카테고리의 다른 글
| 각속도 벡터 (0) | 2021.04.13 |
|---|---|
| 좌표변환 방법 비교 (0) | 2021.02.08 |
| 짐벌락 (Gimbal Lock) (0) | 2021.02.07 |
| 오일러각 (Euler Angles) (0) | 2021.02.07 |
| 방향코사인행렬 (DCM) (1) | 2021.02.06 |




댓글