각속도 벡터

각속도 벡터(angular velocity vector)는 어떤 좌표계를 기준으로 다른 좌표계가 회전 운동할 때, 회전축과 회전 속력을 나타내기 위한 벡터다.

 

 

각속도 벡터의 크기는 회전 속력의 크기인 각속력을 나타내고, 각속도 벡터의 방향은 기준 좌표계에 대하여 회전 운동하는 좌표계의 순간적인 회전축 방향을 나타낸다. 각속력의 크기뿐만 아니라 회전축 방향도 순간순간 변할 수 있으므로 각속도 벡터는 시간의 함수다.

좌표계 $\{b\}$가 좌표계 $\{a\}$를 기준으로 회전 운동할 때, 좌표계 $\{a\}$에서 본 좌표계 $\{b\}$의 각속도 벡터는 ${}^a{\overrightarrow{\omega }}^b$로 표기한다.

 

 

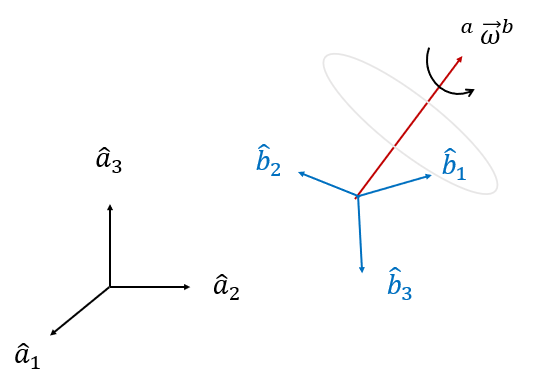
예를 들어서 원판이 점 $O$를 중심으로 일정한 각속력 ${\omega }_0$로 회전하고 있고, 원판의 중심 $O$를 원점으로 하는 정지해 있는 좌표계 $\{a\}$와 원판에 부착되어 원판과 함께 회전하는 원판 좌표계 $\{b\}$가 있다고 하자.

 

 

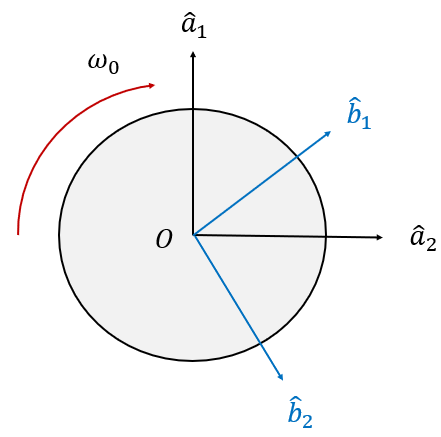
그러면 회전축은 ${\hat{a}}_3$ 또는 ${\hat{b}}_3$이고 각속력은 ${\omega }_0$이므로, 좌표계 $\{a\}$에서 본 좌표계 $\{b\}$의 각속도 벡터는

 

$${}^a{\overrightarrow{\omega }}^b={\omega }_0{\hat{a}}_3={\omega }_0{\hat{b}}_3$$

 

이다.

좌표계 $\{a\}$에서 본 좌표계 $\{b\}$의 각속도가 ${}^a{\overrightarrow{\omega }}^b$이므로, 반대로 좌표계 $\{b\}$에서 본 좌표계 $\{a\}$의 각속도는 ${}^b{\overrightarrow{\omega }}^a$가 되며, 직관적으로 ${}^a{\overrightarrow{\omega }}^b$와 ${}^b{\overrightarrow{\omega }}^a$는 서로 역의 관계에 있다고 예상할 수 있다.

 

$${}^a{\overrightarrow{\omega }}^b={-}^b{\overrightarrow{\omega }}^a$$

 

${}^a{\overrightarrow{\omega }}^b$도 벡터이므로 특정 좌표계에 대해서 표현할 수 있다. 좌표계 $\{a\}$에서 본 좌표계 $\{b\}$의 각속도를 좌표계 $\{c\}$로 표현할 경우에 ${\omega }_{ab}^c$로 표기한다. 예를 들어 ${}^a{\overrightarrow{\omega }}^b$가 아래와 같이 좌표계 $\{b\}$로 표현되었을 경우,

 

$${}^a{\overrightarrow{\omega }}^b={\omega }_1{\hat{b}}_1+{\omega }_2{\hat{b}}_2+{\omega }_3{\hat{b}}_3$$

 

벡터 ${\omega }_{ab}^b$는 다음과 같이 쓸 수 있다.

 

$${\omega }_{ab}^b=[{\omega }_1{\omega }_2{\omega }_3{]}^T$$

 

각속도에서도 연쇄법칙이 성립한다. 연쇄법칙은 다음과 같은 것이다.

 

$${}^a{\overrightarrow{\omega }}^c{=}^a{\overrightarrow{\omega }}^b{+}^b{\overrightarrow{\omega }}^c$$

 

좌표계 $\{a\}$에서 본 좌표계 $\{c\}$의 각속도 벡터를 직접 구할 수도 있지만 중간 단계의 좌표계 $\{b\}$를 두고 각각의 각속도 벡터를 계산해서 구할 수도 있다.

 

 

즉 $\{a\}$에서 $\{c\}$로 가는 것은 $\{a\}$에서 $\{b\}$로, 다시 $\{b\}$에서 $\{c\}$로 가는 것과 같다는 뜻이다. 연쇄법칙은 각속도를 직접 구하기 어려운 경우에 매우 유용하게 사용될 수 있다.

 

 

방향코사인행렬, 오일러각, 그리고 쿼터니언