동일한 벡터라도 좌표계가 달라지면 그 표현이 달라진다. 뿐만 아니라 동일한 벡터를 시간 미분할 때도 미분을 수행하는 좌표계가 달라지면 그 값이 달라진다.
예를 들어 어떤 원판의 중심에서 원판 위의 한점을 가리키는 위치 백터 \(\vec{r}\)이 있다고 하자. 이 원판이 회전하고 관찰자 A도 원판의 중심에서 원판과 같이 회전한다고 하자. 그러면 관찰자 A에게는 시간이 흘러도 벡터 \(\vec{r}\)의 크기와 방향이 바뀌지 않고 그대로일 것이므로, 이 벡터를 시간에 대해서 미분한다면 관찰자 A는 그 값을 \(0\)이라고 할 것이다.
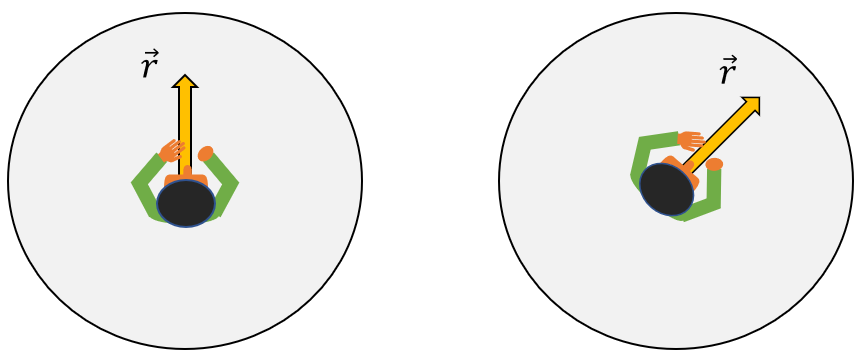
반면에 원판의 중심에 또다른 관찰자 B가 있다고 하자. 관찰자 B는 원판이 회전함에도 불구하고 원판과는 별개로 그대로 있다고 하자(약간 공중 부양해 있다고 가정). 그러면 관찰자 B에게는 시간이 흐름에 따라 벡터 \(\vec{r}\)의 크기는 변하지 않겠지만 방향은 계속 달라질 것이므로, 이 벡터를 시간에 대해서 미분한다면 관찰자 B는 그 값이 \(0\) 이 아니라고 할 것이다.

이 예에서 관찰자 A는 원판에 고정되어 있는 좌표계이고, 관찰자 B는 원판의 외부에 고정되어 있는 좌표계라고 볼 수 있다.
이렇듯 좌표계에 따라서 미분값이 달라지므로 벡터를 시간 미분할 때는 미분을 수행하고자 하는 좌표계를 명시해야 한다.
좌표계 \(\{a\}\)에서 벡터 \(\vec{r}\)의 시간 미분을 \( \frac{^a d\vec{r}}{dt}\)라고 표기한다. \( \frac{^b d\vec{r}}{dt}\)는 좌표계 \(\{b\}\)에서의 벡터 \(\vec{r}\)의 시간 미분을 의미한다. 동일한 벡터를 서로 다른 좌표계에서 미분하면 다른 결과가 얻어지므로 일반적으로
\[ \frac{ ^a d\vec{r}}{dt} \ne \frac{ ^b d\vec{r}}{dt} \]
이다.
임의의 벡터 \(\vec{u}\)가 좌표계 \(\{b\}\)로 표현되어 있다고 하자.
\[ \vec{u} = u_1 \hat{b}_1+ u_2 \hat{b}_2 + u_3 \hat{b}_3 \tag{1} \]
좌표계 \(\{b\}\)에서 벡터 \(\vec{u}\)의 시간 미분은 다음과 같다.
\[ \frac{^b d\vec{u}}{dt} = \dot{u}_1 \hat{b}_1+ \dot{u}_2 \hat{b}_2 + \dot{u}_3 \hat{b}_3 \tag{2} \]
좌표계 \(\{b\}\)에서 보았을 때 좌표계 \(\{b\}\)의 좌표축을 나타내는 단위벡터 \(\hat{b}_1, \hat{b}_2, \hat{b}_3\)는 크기와 방향이 변하지 않기 때문에 미분이 간단해졌다.
하지만 벡터 \(\vec{u}\)를 좌표계 \(\{a\}\)에서 시간 미분한다면 다음과 같이 복잡해진다.
\[ \begin{align} \frac{^a d\vec{u}}{dt} &= \dot{u}_1 \hat{b}_1+ \dot{u}_2 \hat{b}_2 + \dot{u}_3 \hat{b}_3 \tag{3} \\ \\ & \ \ + u_1 \frac{^a d\hat{b}_1}{dt} + u_2 \frac{^a d\hat{b}_2}{dt} + u_3 \frac{^a d\hat{b}_3}{dt} \end{align} \]
좌표계 \(\{b\}\)의 좌표축을 나타내는 단위벡터 \(\hat{b}_1, \hat{b}_2, \hat{b}_3\)는 좌표계 \(\{a\}\)에서 보았을 때 크기는 \(1\)로 고정되어 변하지 않지만 방향은 바뀔 수 있기 때문에 미분값이 \(0\)이라고 볼 수 없기 때문이다.
그렇다면 좌표계 \(\{b\}\)의 단위벡터 \(\hat{b}_1, \hat{b}_2, \hat{b}_3\)는 좌표계 \(\{a\}\)에서 보았을 때 왜 방향이 바뀔까. 좌표계 \(\{b\}\)가 좌표계 \(\{a\}\)에서 보았을 때 수평 이동만 한다면 단위벡터의 방향은 바뀌지 않는다. 오직 회전 운동을 할 때만 방향이 바뀐다.
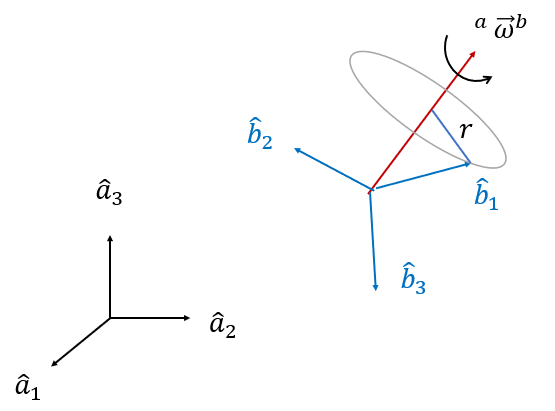
어떤 좌표계가 다른 좌표계에 대해서 상대적인 회전 운동을 한다면 그 운동을 각속도 벡터 \( ^a \vec{\omega}^b\)로 표현할 수 있다.
좌표계 \(\{a\}\)에서 좌표계 \(\{b\}\)의 좌표축 \(\hat{b}_1\)을 시간 미분하면 다음과 같이 된다 (증명은 생략한다).
\[ \frac{^a d\hat{b}_1}{dt}= ^a \vec{\omega}^b \times \hat{b}_1 \tag{4} \]
마찬가지로 다른 좌표축 \(\hat{b}_2\)와 \(\hat{b}_3\)에 대해서도 다음과 같은 관계식이 성립한다. 즉,
\[ \begin{align} & \frac{^a d\hat{b}_2}{dt}= ^a \vec{\omega}^b \times \hat{b}_2 \tag{5} \\ \\ & \frac{^a d\hat{b}_3}{dt}= ^a \vec{\omega}^b \times \hat{b}_3 \end{align} \]
이제 식 (1), (2), (4), (5)를 식 (3)에 대입해 보자. 그러면 다음과 같은 미분 관계식을 얻을 수 있다.
\[ \frac{^a d\vec{u}}{dt}= \frac{^b d\vec{u}}{dt} + ^a \vec{\omega}^b \times \vec{u} \tag{6} \]
이 식은 서로 다른 좌표계에서 수행한 벡터의 시간 미분간의 관계를 나타내 주는 식이다. 이 식을 기본 운동학 방정식 (BKE, Basic Kinematic Equation)이라고 한다. 아주 중요한 식이다.
방향코사인행렬, 오일러각, 그리고 쿼터니언
<b>“좌표계간의 상호 변환관계를 말하다”</b> <b>“물체의 자세 변화를 수학적으로 표현하고 싶은 개발자를 위한 책”</b> 이 책은 방향코사인행렬, 오일러각, 쿼터니언과 이들의 시간 변화율에
digital.kyobobook.co.kr
'항공우주 > 동역학' 카테고리의 다른 글
| 홀로노믹 구속 (Holonomic Constraint)과 가상 변위 (0) | 2021.08.04 |
|---|---|
| 포텐셜 에너지 (Potential Energy) (0) | 2021.08.03 |
| 각속도 벡터 (0) | 2021.04.13 |
| 좌표변환 방법 비교 (0) | 2021.02.08 |
| 쿼터니언 (Quaternions) (0) | 2021.02.08 |




댓글