쿼터니언 (Quaternions)

오일러의 회전 정리(Euler's rotation theorem)에 의하면 모든 좌표변환은 어떤 회전축과 그 회전축을 중심으로 하는 한번의 회전을 통해서 가능하다. 쿼터니언(quaternions)의 정의는 이 회전축과 회전각에 기반을 두고 있다.

 

 

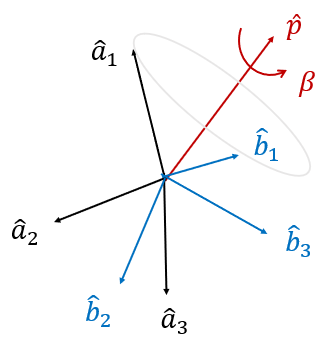
좌표계 $\{a\}$를 회전축 $\hat{p}$ 를 중심으로 회전각 $\beta$ 만큼 회전하여 좌표계 $\{b\}$로 변환했다고 하면, 좌표계 $\{a\}$에서 좌표계 $\{b\}$로의 쿼터니언 $q_b^a$는 다음과 같이 정의된다.

 

$$q_b^a=\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\left[\begin{array}{c}\cos \left(\frac{\beta }{2}\right)\\ p_1\sin \left(\frac{\beta }{2}\right)\\ p_2\sin \left(\frac{\beta }{2}\right)\\ p_3\sin \left(\frac{\beta }{2}\right)\end{array}\right]$$

 

여기서

 

$${\mathbf{p}}^a={\mathbf{p}}^b=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]$$

 

이다. 쿼터니언은 정의와 같이 4개의 실수값으로 구성되어 있기 때문에 사원수라고 번역되기도 한다.

 

 

$q_0$를 쿼터니언의 스칼라부(scalar part)라고 하며 ${\left[\begin{array}{ccc}{q}_1& q_2& q_3\end{array}\right]}^T$를 쿼터니언의 벡터부(vector part)라고 한다.

회전축 $\hat{p}$ 를 중심으로 반대 방향으로 회전각 $\beta$ 만큼 회전하면 쿼터니언은

 

$$q_b^a=\left[\begin{array}{c}\cos \left(\frac{\beta }{2}\right)\\ -p_1\sin \left(\frac{\beta }{2}\right)\\ -p_2\sin \left(\frac{\beta }{2}\right)\\ -p_3\sin \left(\frac{\beta }{2}\right)\end{array}\right]$$

 

가 되어 벡터부만 부호가 바뀐다. 이를 켤레 쿼터니언(quaternions conjugate)이라고 하고 기호로 ${\left(q_b^a\right)}^{\star }$ 로 표시한다.

좌표계 $\{b\}$에서 좌표계 $\{a\}$로의 쿼터니언은 벡터 $q$의 위 첨자와 아래 첨자를 반대로 써서 $q_a^b$로 표현할 수 있다. $q_b^a$와 $q_a^b$는 서로 역변환 관계로서 $q_a^b={\left(q_b^a\right)}^{\star }$의 식이 성립한다.

 

 

쿼티니언 $q$와 $r$의 곱셈을 다음과 같이 벡터와 행렬 형식으로 정의할 수 있다. 쿼터니언 곱셈은 $\otimes$로 표기한다.

 

$$\begin{array}{rl}q\otimes r& =\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]\otimes \left[\begin{array}{c}{r}_0\\ r_1\\ r_2\\ r_3\end{array}\right]\\ \\ & =\left[\begin{array}{cccc}{q}_0& -q_1& -q_2& -q_3\\ q_1& q_0& -q_3& q_2\\ q_2& q_3& q_0& -q_1\\ q_3& -q_2& q_1& q_0\end{array}\right]\left[\begin{array}{c}{r}_0\\ r_1\\ r_2\\ r_3\end{array}\right]\\ \\ & =\left[q\right]r\end{array}$$

 

여기서 $\left[q\right]$을 쿼터니언 행렬이라고 한다.

쿼티니언은 본래 아일랜드의 수학자 해밀턴(William R. Hamilton)이 1843년에 복소수를 확장시켜 만든 수체계(number system)다. 복소수가 2차원 평면상의 점을 표현할 수 있다는 사실로부터 3차원 공간상의 점을 표현하는 방법을 찾다가 만들었다고 한다. 쿼터니언 곱셈도 쿼터니언 수체계의 기본 규칙에서 파생되었다.

 

 

쿼터니언의 정의에 의해서 다음 3가지 성질이 파생된다.

먼저, 벡터 $\overrightarrow{u}$를 좌표계 $\{a\}$로 표현한 벡터 ${\mathbf{u}}^a$와 좌표계 $\{b\}$로 표현한 ${\mathbf{u}}^b$는 다음 관계가 있다.

 

$${\overline{\mathbf{u}}}^a=q_b^a\otimes {\overline{\mathbf{u}}}^b\otimes {\left(q_b^a\right)}^{\star }$$

 

여기서 ${\overline{\mathbf{u}}}^a$는 쿼터니언이 $4\times 1$ 벡터임을 감안하여 벡터 ${\mathbf{u}}^a$를 쿼터니언 벡터화한 것으로 다음과 같이 정의한다.

 

$${\overline{\mathbf{u}}}^a=\left[\begin{array}{c}0\\ {\mathbf{u}}^a\end{array}\right]$$

 

위 식에 의하면 쿼터니언 $q_b^a$는 좌표계 $\{b\}$에서 표현한 벡터 ${\mathbf{u}}^b$를 좌표계 $\{a\}$에서 표현한 벡터 ${\mathbf{u}}^a$로 변환해 준다.

쿼터니언의 두번째 성질은 쿼터니언의 크기가 1이라는 것이다. 즉,

 

$$\begin{array}{rl}{\left(q_b^a\right)}^T{q}_b^a& ={\cos }^2\left(\frac{\beta }{2}\right)+{\left({\mathbf{p}}^a\right)}^T{\mathbf{p}}^a{\sin }^2\left(\frac{\beta }{2}\right)\\ \\ & =1\end{array}$$

 

여기서 ${\mathbf{p}}^a$는 회전축 방향을 표시하는 단위 벡터이기 때문에 크기는 1이다.

쿼터니언의 세번째 성질은 연쇄법칙이 성립한다는 것이다. 연쇄법칙은 다음과 같은 것이다.

 

$$q_c^a=q_b^a\otimes q_c^b$$

 

좌표계 $\{a\}$에서 좌표계 $\{c\}$로의 쿼터니언을 직접 계산할 수도 있지만 중간 단계의 좌표계 $\{b\}$를 두고 각각의 쿼터니언을 계산해서 구할 수도 있다는 이야기다. 즉 $\{a\}$에서 $\{c\}$로 가는 것은 $\{a\}$에서 $\{b\}$로, 다시 $\{b\}$에서 $\{c\}$로 가는 것과 같다는 뜻이다.

 

 

쿼터니언의 첫번째 성질을 증명하려면 좀 복잡한 과정을 거쳐야 하므로 증명은 하지 않겠다. 세번째 성질은 첫번째 성질을 이용하면 쉽게 증명할 수 있다. 쿼터니언에 관한 자세한 사항은 다음 책을 참고하면 좋을 것 같다.

 

 

방향코사인행렬, 오일러각, 그리고 쿼터니언