복소수는 실수부와 허수부를 갖는 수체계다.
실수부를

여기서
오일러 공식(Euler formula)에 의하면 다음 식이 성립하므로,
복소수는 다음과 같이 쓸 수 있다.
두 개의 복소수
곱셈의 결과 복소수의 크기는 두 복소수의 크기를 곱한 것과 같고 위상각은 더한 것과 같다.
일반적인 정방 행렬에서 고유값(eigenvalue)과 고유벡터(eigenvector)는 복소수 값을 가질 수 있다. 만약 실수 행렬이라면 고유값과 고유벡터가 복소수일때, 그 켤레 복소수(complex conjugate)도 고유값과 고유벡터가 된다. 증명은 다음과 같다.
먼저 정방 행렬
여기서
여기서 바(bar)는 켤레 복소수를 나타내는 기호이다.
식 (3)에 의하면
상태변수의 미분 방정식으로 표현되는 어떤 시스템의 운동 방정식,
의 해는 다음과 같이 주어진다.
여기서
그런데 여기서 고유값이 복소수로 나오면 어떻게 될까.
식 (5)에서 고유값
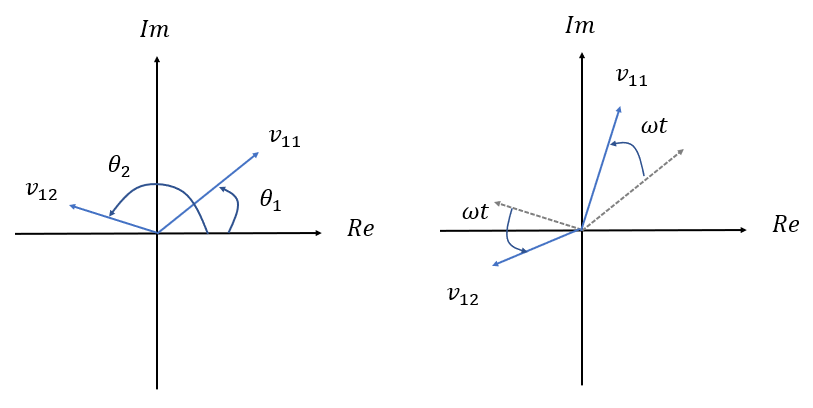
그러면 고유값에 대응하는 고유벡터도 서로 켤레 복소수인 벡터가 된다. 곱셈에서는 복소수를 크기와 위상각 형태로 쓰는 것이 유리하므로 고유벡터는 다음과 같이 표현한다.
상태변수 벡터
이제 식 (6), (7), (8)을 식 (5) 대입하면 다음과 같이 된다.
식 (9)에 의하면 고유값이 복소수일 때 시스템은 진동하며 진동 주파수
상태변수의 상대적인 진동 크기는 다음 그림으로 표현할 수 있다.
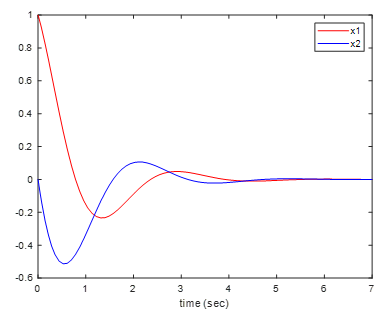
시뮬레이션 예를 들어보자. 시스템의 운동 방정식과 초기값이 다음과 같을 때,
고유값과 고유벡터는 각각 다음과 같다.
시스템의 반응은 다음 그림과 같이 감쇠있는 진동 운동을 한다.
운동 방정식 (4)에서
예를 들어
만약 고유값이 켤레 복소수
고유값이 모두 실수값으로 나온다면 진동 없는
'유도항법제어 > 비행제어' 카테고리의 다른 글
| 주파수 응답 (0) | 2021.02.05 |
|---|---|
| 정정상태 응답과 과도 응답 (0) | 2021.02.05 |
| 운동 모드 해석 (0) | 2021.01.26 |
| [Continuous-Time] 선형 시스템 (0) | 2021.01.10 |
| 시스템의 수학적 표현 방법 (0) | 2021.01.09 |




댓글