주파수 응답(frequency response)은 안정한 LTI(선형 시불변) 시스템에 싸인 또는 코사인 파형(sinusoids) 입력을 가했을 때 나오는 정정상태 응답(steady-state response)이다.
입력 \(u(t)\)가 시스템에 가해지는 시간이 \(t=-\infty\) 이라면 인과(causal) LTI 시스템의 출력은 다음과 같다.
\[ y(t)= \int_{-\infty}^t h(t-\tau) u(\tau) \ d\tau \]
여기서 \(h(t)\)는 LTI 시스템의 임펄스 반응(impulse response)이다.
위 식에 의하면 시스템에 입력이 가해진 지 이미 무한대의 시간이 경과했으므로 시스템이 안정하다면, 시간 \(t\)에서의 반응은 이미 정정상태에 도달했다고 볼 수 있다.
이제 입력이 다음과 같이 진폭이 \(A\)고 주파수가 \(\omega\)인 sinusoids라고 하자.
\[ u(t)=A e^{j \omega t} \]
그러면 정정상태 출력은 다음과 같이 계산된다.
\[ \begin{align} y(t) &= \int_{-\infty}^t h(t-\tau) u(\tau) \ d\tau \\ \\ &= \int_0^\infty h(\tau) u(t-\tau) \ d\tau \\ \\ &= \int_0^\infty h(\tau) Ae^{j \omega (t-\tau)} \ d\tau \\ \\ &= Ae^{j \omega t} \int_0^\infty h(\tau) e^{-j \omega \tau } \ d\tau \end{align} \]
위 식에서 적분 부분은 \(h(\tau)\)의 라플라스 변환(Laplace transform) \(H(s)\)에서 \(s=j \omega \) 로 치환한 것과 같으므로
\[ y(t)=H(j \omega) Ae^{j \omega t} \]
가 된다. 여기서
\[ H(s) = \mathfrak{L} \left[ h(t) \right] = \int_0^\infty h(t) e^{-st} \ dt \]
이다. 안정한 LTI 시스템에 sinusoids 입력을 가했을 때 나오는 정정상태 응답이 주파수 응답인데, 위 식에 의하면 이 응답은 \(H(j \omega)\)만 알면 계산할 수 있기 때문에 \(H(j \omega )\)를 주파수 응답이라고 하기도 한다.
주파수 응답의 예를 들어 보자.
시스템의 전달함수가 \(H(s)= \frac{1}{(s+1)}\) 일 때, 입력이 \(u(t)= \sin (0.5t) \)라면,
주파수 응답은 다음과 같고,
\[ H(j0.5) = \frac{1}{(j0.5+1)} \]
정정상태 응답은 다음과 같이 된다.
\[ \begin{align} y(t) &= \mathit{Im} \left[ H(j0.5) e^{j0.5t} \right] \\ \\ &= \left\vert H(j0.5) \right\vert \sin (0.5t+\angle H(j0.5)) \end{align} \]
여기서 \(\mathit{Im}\)은 복소수의 허수부를 뜻하고,
\[ \begin{align} & \left\vert H(j0.5) \right\vert = \left\vert \frac{1}{(j0.5+1)} \right\vert \approx 0.9 \\ \\ & \angle H(j0.5) = -\tan^{-1} 0.5 \approx -26.6^o \end{align} \]
이다. 따라서 정정상태 응답은 다음과 같이 된다.
\[ y(t) \approx 0.9 \sin(0.5t-26.6^o ) \]
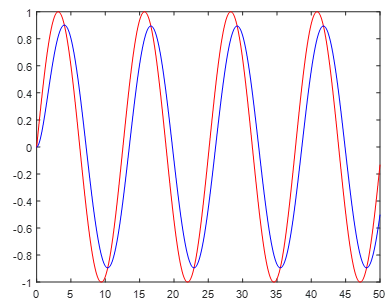
위 그림에서 빨강색이 입력, 파랑색이 응답이다.
'유도항법제어 > 제어일반' 카테고리의 다른 글
| [Continuous-Time] LTI 시스템과 컨볼루션 (0) | 2022.09.13 |
|---|---|
| [Continuous-Time] LTI 시스템 (0) | 2022.09.13 |
| 주파수 응답 (0) | 2021.02.05 |
| 정정상태 응답과 과도 응답 (0) | 2021.02.05 |
| 진동 모드 해석 (0) | 2021.01.26 |
| 운동 모드 해석 (0) | 2021.01.26 |
댓글0