[CR3BP] 라그랑지 포인트 안정성 해석

CR3BP의 무차원화된 운동방정식은 다음과 같았다 (https://pasus.tistory.com/147).

 

$$\begin{array}{r}\text{(1)}& & \ddot{x}-2\dot{y}=-{\overline{U}}_x\\ & \ddot{y}+2\dot{x}=-{\overline{U}}_y\\ \\ & \ddot{z}=-{\overline{U}}_z\end{array}$$

여기서

$$\begin{array}{rl}& U_{eff}=-\frac{1}{2}(x^2+y^2)-\frac{1-\mu }{r_1}-\frac{\mu }{r_2}-\frac{1}{2}\mu (1-\mu )\\ \\ & r_1=\sqrt{(x+\mu {)}^2+y^2+z^2}\\ \\ & r_2=\sqrt{(x+\mu -1{)}^2+y^2+z^2}\\ \\ & {\overline{U}}_x=\frac{\partial U_{eff}}{\partial x},{\overline{U}}_y=\frac{\partial U_{eff}}{\partial y},{\overline{U}}_z=\frac{\partial U_{eff}}{\partial z}\end{array}$$

 

이다.

 

 

라그랑지 포인트(Lagrange point) 의 안정성(stability)을 분석하기 위해 평형점인 각 라그랑지 포인트 $(x_0,y_0,0)$ 에서 미소 변위 $(\delta x,\delta y,\delta z)$ 를 고려하자. 그리고 식 (1)에 $x=x_0+\delta x,y=y_0+\delta y,z=\delta z$ 를 대입하고 테일러 시리즈로 전개한다. 일단 식 (1)에서 ${\overline{U}}_x,{\overline{U}}_y,{\overline{U}}_z$ 부터 전개해 보자.

 

$$\begin{array}{r}\text{(2)}& & {\overline{U}}_x=({\overline{U}}_x{)}_0+{\overline{U}}_{xx}\delta x+{\overline{U}}_{xy}\delta y+{\overline{U}}_{xz}\delta z+\cdots \\ & {\overline{U}}_y=({\overline{U}}_y{)}_0+{\overline{U}}_{xy}\delta x+{\overline{U}}_{yy}\delta y+{\overline{U}}_{yz}\delta z+\cdots \\ \\ & {\overline{U}}_z=({\overline{U}}_z{)}_0+{\overline{U}}_{xz}\delta x+{\overline{U}}_{yz}\delta y+{\overline{U}}_{zz}\delta z+\cdots \end{array}$$

 

여기서 아래 첨자 ${}_0$ 은 평형점에서 미분을 계산한다는 뜻이고,

 

$$\begin{array}{r}\text{(3)}& & {\overline{U}}_{xx}={\left(\frac{{\partial }^2{U}_{eff}}{\partial x^2}\right)}_0,{\overline{U}}_{yy}={\left(\frac{{\partial }^2{U}_{eff}}{\partial y^2}\right)}_0,{\overline{U}}_{zz}={\left(\frac{{\partial }^2{U}_{eff}}{\partial z^2}\right)}_0\\ & {\overline{U}}_{xy}={\left(\frac{{\partial }^2{U}_{eff}}{\partial x\partial y}\right)}_0,{\overline{U}}_{xz}={\left(\frac{{\partial }^2{U}_{eff}}{\partial x\partial z}\right)}_0,{\overline{U}}_{yz}={\left(\frac{{\partial }^2{U}_{eff}}{\partial y\partial z}\right)}_0\end{array}$$

 

이다. 라그랑지 포인트, 즉 평형점에서는 $\ddot{x}=\dot{x}=\ddot{y}=\dot{y}=\ddot{z}=\dot{z}=0$ 이므로 식 (1)에 의하면 $({\overline{U}}_x{)}_0=({\overline{U}}_y{)}_0=({\overline{U}}_z{)}_0=0$ 이다. 따라서 식 (2)를 (1)에 대입하면 다음과 같이 선형화 식을 얻을 수 있다.

 

$$\begin{array}{r}\text{(4)}& & \delta \ddot{x}-2\delta \dot{y}=-{\overline{U}}_{xx}\delta x-{\overline{U}}_{xy}\delta y-{\overline{U}}_{xz}\delta z\\ & \delta \ddot{y}+2\delta \dot{x}=-{\overline{U}}_{xy}\delta x-{\overline{U}}_{yy}\delta y-{\overline{U}}_{yz}\delta z\\ \\ & \delta \ddot{z}=-{\overline{U}}_{xz}\delta x-{\overline{U}}_{yz}\delta y-{\overline{U}}_{zz}\delta z\end{array}$$

 

식 (3)에서 ${\overline{U}}_{xz}$ 와 ${\overline{U}}_{yz}$ 를 계산해보면 다음과 같다.

 

$$\begin{array}{r}\text{(5)}& & {\overline{U}}_{xz}=-\frac{3(1-\mu )(x_0+\mu )}{(r_1^5{)}_0}{z}_0-\frac{3\mu (x_0+\mu -1)}{(r_2^5{)}_0}{z}_0=0\\ & {\overline{U}}_{yz}=-\frac{3(1-\mu )y_0}{(r_1^5{)}_0}{z}_0-\frac{3\mu y_0}{(r_2^5{)}_0}{z}_0=0\end{array}$$

여기서

$$\begin{array}{rl}& (r_1^5{)}_0=((x_0+\mu {)}^2+y_0^2{)}^{5/2}\\ \\ & (r_2^5{)}_0=((x_0+\mu -1{)}^2+y_0^2{)}^{5/2}\end{array}$$

 

이다. 식 (5)를 (4)에 대입하면 선형화 식은 다음과 같이 된다.

 

$$\begin{array}{r}\text{(7)}& & \delta \ddot{x}-2\delta \dot{y}=-{\overline{U}}_{xx}\delta x-{\overline{U}}_{xy}\delta y\\ & \delta \ddot{y}+2\delta \dot{x}=-{\overline{U}}_{xy}\delta x-{\overline{U}}_{yy}\delta y\\ \\ & \delta \ddot{z}=-{\overline{U}}_{zz}\delta z\end{array}$$

 

식 (7)에 의하면 $\delta z$ 방정식은 $\delta x,\delta y$ 방정식과 독립적이므로 별도로 취급할 수 있다. 먼저 식 (7)에서 ${\overline{U}}_{zz}$ 를 계산한다.

 

$$\begin{array}{r}\text{(8)}& {\overline{U}}_{zz}& =-\frac{3(1-\mu )}{(r_1^5{)}_0}{z}_0^2-\frac{3\mu }{(r_2^5{)}_0}{z}_0^2+\frac{(1-\mu )}{(r_1^3{)}_0}+\frac{\mu }{(r_2^3{)}_0}\\ & =\frac{(1-\mu )}{(r_1^3{)}_0}+\frac{\mu }{(r_2^3{)}_0}\end{array}$$

여기서

$$\begin{array}{rl}& (r_1^3{)}_0=((x_0+\mu {)}^2+y_0^2{)}^{3/2}\\ \\ & (r_2^3{)}_0=((x_0+\mu -1{)}^2+y_0^2{)}^{3/2}\end{array}$$

 

이다. 식 (8)에 의하면 ${\overline{U}}_{zz}>0$ 이다. 따라서 $\delta z$ 방정식의 해는 다음과 같다. /span>

 

$$\begin{array}{}\text{(9)}& \delta z(t)=A_z\sin (\sqrt{{\overline{U}}_{zz}}t+{\psi }_z)\end{array}$$

 

여기서 $A_z$ 와 ${\psi }_z$ 는 초기값에 따라 결정되는 상수이다.

이제 식 (7)에서 $\delta x,\delta y$ 방정식의 해를 구하기 위해서 식을 다음과 같이 상태 미분 방정식으로 바꾼다.

 

$$\begin{array}{r}\text{(10)}& & \delta \dot{x}=\delta v_x\\ & \delta \dot{y}=\delta v_y\\ \\ & \delta {\dot{v}}_x=2\delta v_y-{\overline{U}}_{xx}\delta x-{\overline{U}}_{xy}\delta y\\ \\ & \delta {\dot{v}}_y=-2\delta v_x-{\overline{U}}_{xy}\delta x-{\overline{U}}_{yy}\delta y\end{array}$$

 

$\delta x,\delta y$ 운동은 결합되어 있기 때문에 다음과 같이 벡터 형식으로 바꾸는 것이 편리하다.

 

$$\begin{array}{}\text{(11)}& \dot{\mathbf{w}}=A\mathbf{w}\end{array}$$

여기서

$$A=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -{\overline{U}}_{xx}& -{\overline{U}}_{xy}& 0& 2\\ -{\overline{U}}_{xy}& -{\overline{U}}_{yy}& -2& 0\end{array}\right],\mathbf{w}=\left[\begin{array}{c}\delta x\\ \delta y\\ \delta v_x\\ \delta v_y\end{array}\right]$$

 

이다. 위 식을 풀면 다음과 같다.

 

$$\begin{array}{}\text{(12)}& \left[\begin{array}{c}\delta x(t)\\ \delta y(t)\\ \delta v_x(t)\\ \delta v_y(t)\end{array}\right]=e^{At}\left[\begin{array}{c}\delta x_0\\ \delta y_0\\ \delta v_{x_0}\\ \delta v_{y_0}\end{array}\right]\end{array}$$

 

여기서 $\delta x_0,\delta y_0,\delta v_{x_0},\delta v_{y_0}$ 는 각각 $\delta x,\delta y,\delta v_x,\delta v_y$ 의 초기값이다.

 

 

식 (11)에서 행렬 $A$ 의 특성방정식을 구해보면 다음과 같다.

 

$$\begin{array}{r}\text{(13)}& det(A-& \lambda I)=det\left[\begin{array}{cccc}-\lambda & 0& 1& 0\\ 0& -\lambda & 0& 1\\ -{\overline{U}}_{xx}& -{\overline{U}}_{xy}& -\lambda & 2\\ -{\overline{U}}_{xy}& -{\overline{U}}_{yy}& -2& -\lambda \end{array}\right]\\ & ={\lambda }^4+(4+{\overline{U}}_{xx}+{\overline{U}}_{yy}){\lambda }^2+{\overline{U}}_{xx}{\overline{U}}_{yy}-{\overline{U}}_{xy}^2\\ \\ & =0\end{array}$$

 

위 특성방정식의 해는 ${\overline{U}}_{xx},{\overline{U}}_{yy},{\overline{U}}_{xy}$ 를 계산해야 알 수 있다.

 

$$\begin{array}{rl}\text{(14)}& & {\overline{U}}_{xx}=-1-\frac{3(1-\mu )(x_0+\mu {)}^2}{(r_1^5{)}_0}-\frac{3\mu (x_0+\mu -1{)}^2}{(r_2^5{)}_0}& +\frac{(1-\mu )}{(r_1^3{)}_0}+\frac{\mu }{(r_2^3{)}_0}\\ \\ & {\overline{U}}_{yy}=-1-\frac{3(1-\mu )y_0^2}{(r_1^5{)}_0}-\frac{3\mu y_0^2}{(r_2^5{)}_0}+\frac{(1-\mu )}{(r_1^3{)}_0}+\frac{\mu }{(r_2^3{)}_0}\\ \\ & {\overline{U}}_{xy}=-\frac{3(1-\mu )(x_0+\mu )y_0}{(r_1^5{)}_0}-\frac{3\mu (x_0+\mu -1)y_0}{(r_2^5{)}_0}\end{array}$$

 

이제 라그랑지 포인트 L4 및 L5 안정성부터 분석해 보도록 하자. L4 및 L5 포인트는 위치에너지의 최대값에 해당하는 지점이므로 일반적으로 불안정한 평형 상태일 것으로 생각할 수 있는데, 안정성 해석 결과는 예상 밖으로 중립 안정(neutrally stable)이다.

 

 

L4 및 L5 포인트에서는

 

$$(r_1{)}_0=1,(r_2{)}_0=1,x_0=\frac{1}{2}-\mu ,y_0=\pm \frac{\sqrt{3}}{2}$$

 

이므로 식 (14)와 (8)은 다음 값을 갖는다.

 

$$\begin{array}{r}\text{(15)}& & {\overline{U}}_{xx}=-\frac{3}{4},{\overline{U}}_{yy}=-\frac{9}{4}\\ & {\overline{U}}_{xy}=\mp \frac{3\sqrt{3}}{4}(1-2\mu ),{\overline{U}}_{zz}=1\end{array}$$

 

식 (15)를 식 (9)에 대입하면 $\delta z$ 는 다음과 같이 된다.

 

$$\begin{array}{}\text{(16)}& \delta z(t)=A_z\sin (t+{\psi }_z)\end{array}$$

 

또한 식 (15)를 식 (13)에 대입하면 특성방정식은 다음과 같이 된다.

 

$$\begin{array}{}\text{(17)}& {\lambda }^4+{\lambda }^2+\frac{27}{4}\mu (1-\mu )=0\end{array}$$

 

위 식을 풀면 다음과 같다.

 

$$\begin{array}{}\text{(18)}& {\lambda }_{1,3}^2=\frac{-1\pm \sqrt{1-27\mu (1-\mu )}}{2}\end{array}$$

 

위 식에서 $\mathrm{\Delta }=1-27\mu (1-\mu )$ 의 값이 양수인지 음수인지에 따라서 ${\lambda }^2$ 이 실수 또는 복소수가 되므로 두 경우를 분리해서 분석하기로 한다.

먼저 $\mathrm{\Delta }<0$ 인 경우에는 ${\lambda }^2$ 는 복소수가 된다.

 

$$\begin{array}{}\text{(19)}& {\lambda }_{1,3}^2=\frac{-1\pm j\sqrt{|\mathrm{\Delta }|}}{2}\end{array}$$

 

그러면 $\lambda$ 는 다음과 같이 계산된다.

 

$$\begin{array}{r}\text{(20)}& & {\lambda }_1=a_1+j{b}_1,{\lambda }_2=-a_1-j{b}_1\\ & {\lambda }_3=a_2+j{b}_2,{\lambda }_4=-a_2-j{b}_2\end{array}$$

 

위 식에 의하면

 

$$\begin{array}{rl}{\lambda }_1^2& =(a_1+j{b}_1{)}^2=a_1^2-b_1^2+j2a_1{b}_1\\ \\ & =-\frac{1}{2}+j\frac{1}{2}\sqrt{|\mathrm{\Delta }|}\end{array}$$

 

이므로 $a_1\ne 0$ 이어야 한다. 만약 $a_1>0$ 이라면 ${\lambda }_1$ 은 양의 실수부를 갖기 때문에 L4 및 L5 포인트는 불안정하다. 또한 만약 $a_1<0$ 이라면 이번에는 ${\lambda }_2$ 가 양의 실수부를 갖기 때문에 역시 불안정하다. 따라서 L4 및 L5 포인트가 안정하려면 $\mathrm{\Delta }\ge 0$ 이어야 한다. 또한 식 (18)에서 ${\lambda }^2>0$ 이면 양의 실수부를 갖는 $\lambda$ 이 하나 이상 존재하기 때문에 역시 불안정하다. 따라서 L4 및 L5 포인트가 불안정하지 않으려면 ${\lambda }^2<0$ 이어야 한다. 즉,

 

$$\begin{array}{}\text{(21)}& 0\le 1-27\mu (1-\mu )<1\end{array}$$

 

$0<\mu \le 1/2$ 이므로 식 (21)을 만족하는 $\mu$ 의 범위는 다음과 같다.

 

$$\begin{array}{}\text{(22)}& \mu \le \frac{1}{2}-\frac{1}{2}\sqrt{\frac{23}{27}}\approx 0.03852\end{array}$$

 

따라서 L4 및 L5 포인트의 (중립) 안정성을 위해서는 $\mu \le 0.03852$ 가 필요한데 이는 태양계에서는 항상 만족하는 값이다.

 

 

L4 및 L5 포인트가 안정한 평형점이므로 소행성 등 작은 천체에 안정적인 위치를 제공할 수 있을 것으로 예상되는데, 실제로 태양-목성 시스템의 L4 및 L5 포인트에 많은 소행성들이 몰려 있는 목성 트로이 군(Jupiter Trojan)이 확인되었다. 또한 태양-화성, 태양-금성, 태양-천왕, 태양-해왕성 시스템에도 트로이 소행성이 발견되었다.

 

 

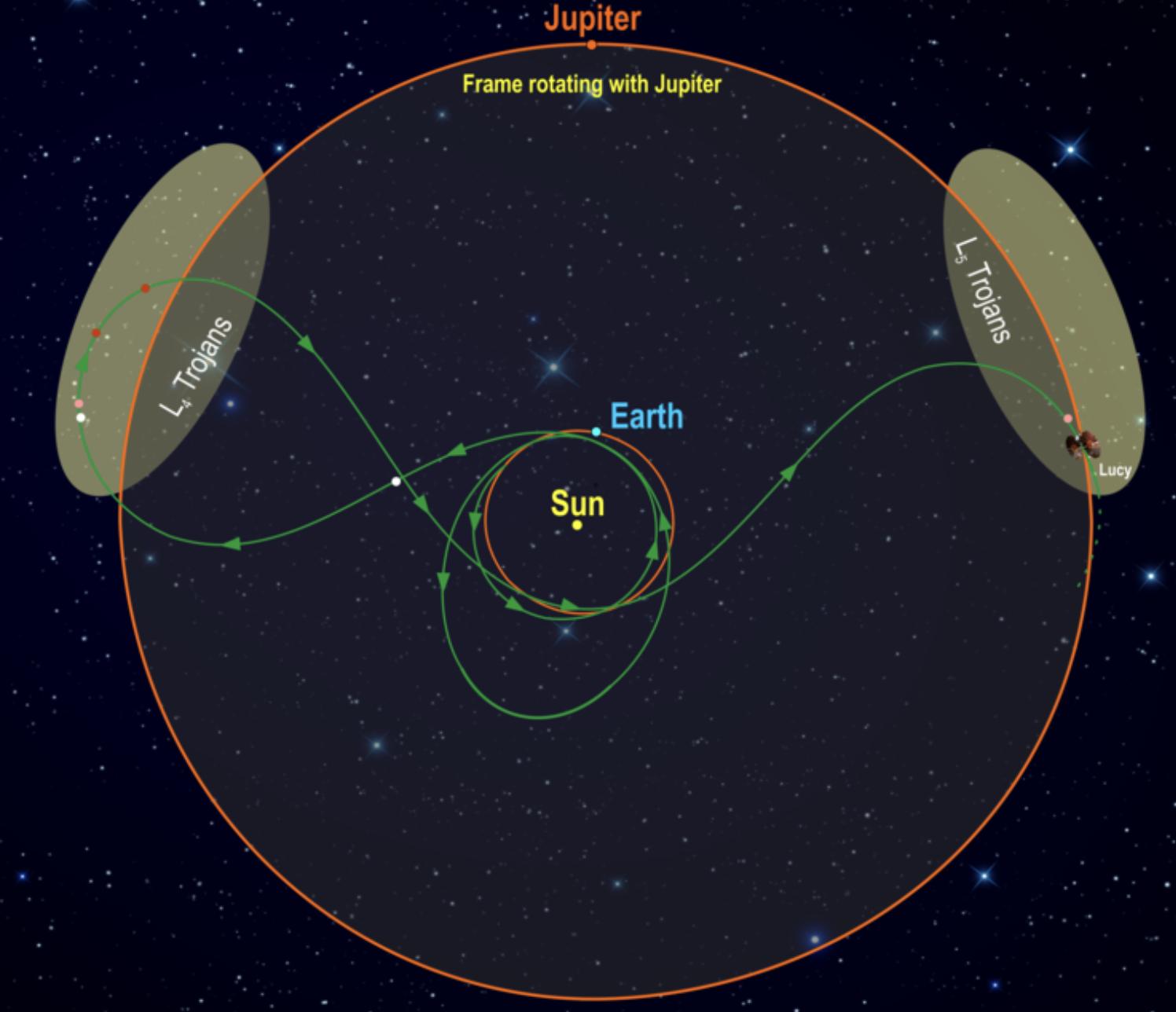
지구-달 시스템의 경우 $\mu =0.0121505$ 이므로 L4 및 L5 포인트는 안정하지만 트로이 소행성은 발견되지 않았다. 태양 중력의 영향이 크기 때문에 CR3BP의 가정이 잘 들어맞지 않은 것으로 보인다.

이번에는 라그랑지 포인트 L1, L2 및 L3 안정성에 대해 알아보도록 하자.

 

 

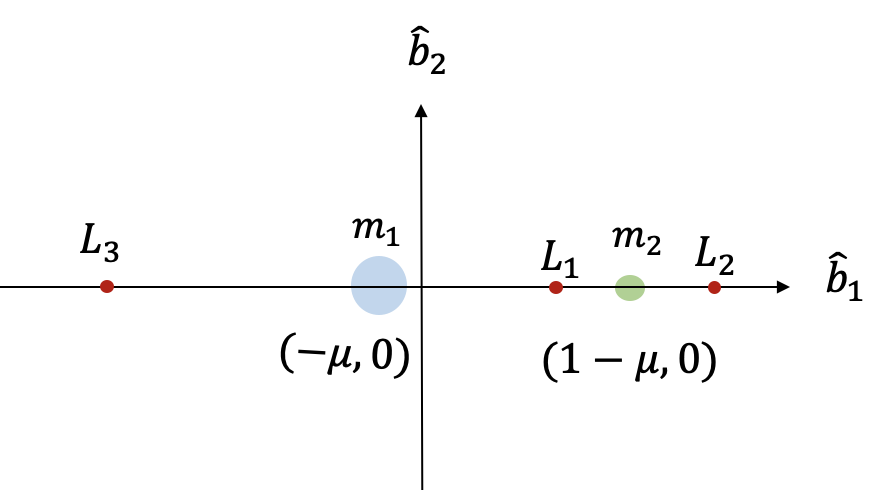
L1, L2 및 L3 포인트에서는 $y_0=0$ 이므로, 식 (14)와 식 (8)은 다음과 같이 계산된다.

 

$$\begin{array}{r}\text{(23)}& & {\overline{U}}_{xx}=-1-\frac{2(1-\mu )}{|x_0+\mu {|}^3}-\frac{2\mu }{|x_0+\mu -1{|}^3}\\ & {\overline{U}}_{yy}=-1+\frac{(1-\mu )}{|x_0+\mu {|}^3}+\frac{\mu }{|x_0+\mu -1{|}^3}\\ \\ & {\overline{U}}_{xy}=0\\ \\ & {\overline{U}}_{zz}=\frac{(1-\mu )}{|x_0+\mu {|}^3}+\frac{\mu }{|x_0+\mu -1{|}^3}\end{array}$$

 

식 (23)을 식 (9)에 대입하면 $\delta z$ 는 다음과 같이 된다.

 

$$\begin{array}{}\text{(24)}& \delta z(t)=A_z\sin (\sqrt{{\overline{U}}_{zz}}t+{\psi }_z)\end{array}$$

 

여기서 ${\overline{U}}_{zz}>0$ 이다. 또한 식 (23)을 식 (13)에 대입하면 특성방정식은 다음과 같이 된다.

 

$$\begin{array}{}\text{(25)}& {\lambda }^4+(2-c_2){\lambda }^2+(1+c_2-2c_2^2)=0\end{array}$$

여기서

$$c_2=\frac{(1-\mu )}{|x_0+\mu {|}^3}+\frac{\mu }{|x_0+\mu -1{|}^3}={\overline{U}}_{zz}$$

 

이다. 식 (25)에 의하면,

 

$$\begin{array}{}\text{(26)}& {\lambda }_1^2{\lambda }_3^2=1+c_2-2c_2^2=(1+2c_2)(1-c_2)\end{array}$$

 

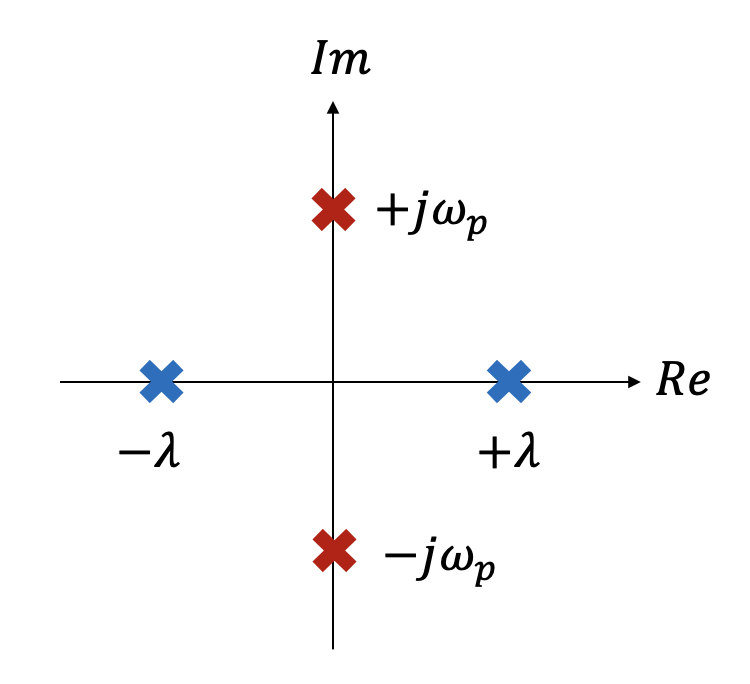
이다. 그런데 ${\lambda }_2=-{\lambda }_1,{\lambda }_4=-{\lambda }_3$ 이므로 라그랑지 포인트가 안정하려면 ${\lambda }_i$ 가 모두 허수이어야 한다. 즉 ${\lambda }_1^2<0$ 이고 ${\lambda }_3^2<0$ 이어야 한다. 그러기 위해서는 식 (26)에서 $c_2<1$ 이어야 하는데 L1, L2 및 L3 포인트에서는 모두 $c_2>1$ 이다.

따라서 L1, L2 및 L3 포인트에서는 ${\lambda }_1^2>0$, ${\lambda }_3^2<0$ 이 되므로 특성방정식의 근 또는 식 (11)의 행렬 $A$ 의 고유값(eigenvalue)은 다음과 같이 두 개의 실수, 두 개의 허수가 되므로 L1, L2 및 L3 포인트는 $\mu$ 값에 관계없이 모두 불안정한 평형점이다.