Clohessy-Wiltshire(CW) 방정식을
\[ \begin{align} & \ddot{x}-3n^2 x-2n \dot{y}=f_1 \tag{1} \\ \\ & \ddot{y}+2n \dot{x}=f_2 \\ \\ & \ddot{z}+n^2 z=f_3 \end{align} \]
벡터 행렬식으로 표현하면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{z} \\ \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{bmatrix} =\begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 3n^2 & 0 & 0 & 0 & 2n & 0 \\ 0 & 0 & 0 & -2n & 0 & 0 \\ 0 & 0 & n^2 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \dot{x} \\ \dot{y} \\ \dot{z} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 0 \\ f_1 \\ f_2 \\ f_3 \end{bmatrix} \tag{2} \\ \\ \to & \ \ \ \dot{\mathbf{x}}=A \mathbf{x}+ \begin{bmatrix} 0 \\ \mathbf{f} \end{bmatrix} \end{align} \]
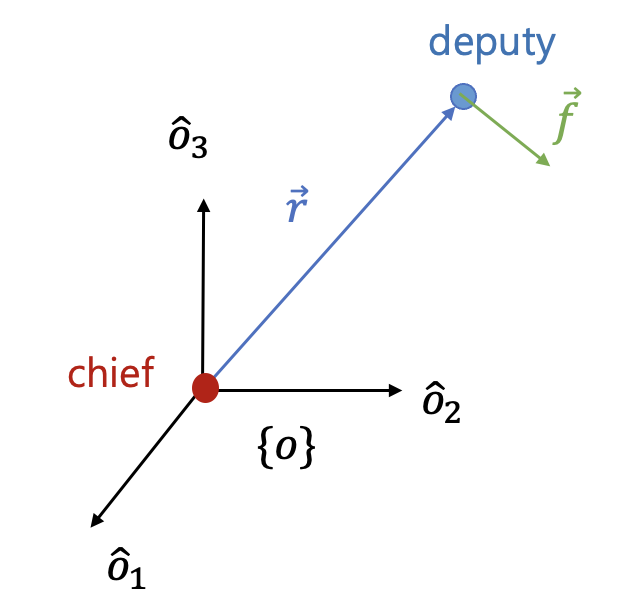
섭동력(perturbing specific force)이 모두 \(0\) 이라는 가정하에 위 식을 풀면 다음과 같았다 (https://pasus.tistory.com/240).
\[ \begin{align} & \begin{bmatrix} x(t) \\ y(t) \\ z(t) \\ \dot{x}(t) \\ \dot{y}(t) \\ \dot{z}(t) \end{bmatrix} = \begin{bmatrix} 1 & 0 & -\cos nt & -\sin nt & 0 & 0 \\ -\frac{3}{2} nt & 1 & 2 \sin nt & -2 \cos nt & 0 & 0 \\ 0 & 0 & 0 & 0 & \sin nt & -\cos nt \\ 0 & 0 & n \sin nt & -n \cos nt & 0 & 0 \\ -\frac{3}{2} n & 0 & 2n \cos nt & 2n \sin nt & 0 & 0 \\ 0 & 0 & 0 & 0 & n \cos nt & n \sin nt \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \end{bmatrix} \tag{3} \\ \\ \to & \ \ \ \mathbf{x}(t)=S(t) \mathbf{c} \end{align} \]
여기서 \(c_1, ... , c_6\) 는 초기값의 조합으로 이루어진 상수다. 위 식의 역행렬을 구하면 상수항을 시간 \(t\) 에서의 상대 위치와 속도로 표현할 수 있다.
\[ \begin{align} & \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \end{bmatrix} = \begin{bmatrix} 4 & 0 & 0 & 0 & \frac{2}{n} & 0 \\ 6nt & 1 & 0 & -\frac{2}{n} & 3t & 0 \\ 3 \cos nt & 0 & 0 & \frac{1}{n} \sin nt & \frac{2}{n} \cos nt & 0 \\ 3 \sin nt & 0 & 0 & -\frac{1}{n} \cos nt & \frac{2}{n} \sin nt & 0 \\ 0 & 0 & \sin nt & 0 & 0 & \frac{1}{n} \cos nt \\ 0 & 0 & -\cos nt & 0 & 0 & \frac{1}{n} \sin nt \end{bmatrix} \begin{bmatrix} x(t) \\ y(t) \\ z(t) \\ \dot{x}(t) \\ \dot{y}(t) \\ \dot{z}(t) \end{bmatrix} \tag{4} \\ \\ \to & \ \ \ \mathbf{c}=S^{-1} (t) \mathbf{x} (t) \end{align} \]
이제 섭동력이 존재하는 경우에 대해서도 CW 방정식을 풀어보자. 풀이를 위해 파라미터 변분법(VOP, variation of parameters)을 도입한다. VOP는 섭동력에 의해 교란된 동적 시스템의 풀이에 적합한 방법이다. 이 방법은 교란되지 않은 시스템 해(solution)의 상수를 시변(time-varying) 파라미터로 일반화할 수 있다면 교란되지 않은 시스템의 해를 사용하여 교란된 시스템의 해를 나타낼 수 있다는 것을 전제로 한다. 즉 식 (3)에서 상수를 시변 파라미터로 간주한다면 식 (3)도 식 (2)의 해가 될 수 있다는 것이다.
식 (3)은 교란되지 않은 시스템의 해이므로 다음 식이 성립한다.
\[ \dot{\mathbf{x}}(t)= \dot{S}(t) \mathbf{c}=A \mathbf{x} \tag{5} \]
식 (3)에서 상수를 시변 파라미터로 간주한다면 식 (3)도 식 (2)의 해가 될 수 있으므로 식 (3)을 (2)에 대입하며 다음과 같이 된다.
\[ \dot{\mathbf{x}}(t)=\dot{S}(t) \mathbf{c}+ S(t) \dot{\mathbf{c}}=A \mathbf{x}+ \begin{bmatrix} 0 \\ \mathbf{f} \end{bmatrix} \tag{6} \]
식 (5)를 이용하면 식 (6)은 다음과 같이 된다.
\[ S(t) \dot{\mathbf{c}}=\begin{bmatrix} 0 \\ \mathbf{f} \end{bmatrix} \tag{7} \]
따라서 \(\dot{\mathbf{c}}\) 은 다음과 같이 구할 수 있다.
\[ \dot{\mathbf{c}}=S^{-1} (t) \begin{bmatrix} 0 \\ \mathbf{f} \end{bmatrix} \tag{8} \]
식 (4)를 이용하면 식 (8)은 다음과 같이 된다.
\[ \begin{bmatrix} \dot{c}_1 \\ \dot{c}_2 \\ \dot{c}_3 \\ \dot{c}_4 \\ \dot{c}_5 \\ \dot{c}_6 \end{bmatrix} = \begin{bmatrix} 0 & \frac{2}{n} & 0 \\ -\frac{2}{n} & 3t & 0 \\ \frac{1}{n} \sin nt & \frac{2}{n} \cos nt & 0 \\ -\frac{1}{n} \cos nt & \frac{2}{n} \sin nt & 0 \\ 0 & 0 & \frac{1}{n} \cos nt \\ 0 & 0 & \frac{1}{n} \sin nt \end{bmatrix} \begin{bmatrix} f_1(t) \\ f_2(t) \\ f_3(t) \end{bmatrix} \tag{9} \]
식 (9)는 섭동력에 대한 상수항의 시간 변화율을 나타내는 식으로서 식 (3)과 함께 상대 궤도 제어 시스템의 동적 모델로 사용할 수 있다. 이 때의 섭동력은 위성의 추진력에 해당한다.
상대 궤도 제어 시스템은 여러 대의 인공위성이 편대를 이루어 임무를 수행하는 동안 대형을 유지하거나 대형을 재구성할 때, 또는 충돌회피 기동을 할 때 필요하다.
위성 추진기는 추진 시간에 따라 연속 추력기과 순간 추력기로 나눌 수 있는데, 연속 추력은 위성의 자세 기동과 결합되어야 하고 현재의 기술로는 발생되는 추력이 너무 작기 때문에 저궤도 임무에 바람직하지 않는 경우가 많다. 순간 추력은 분사시간이 매우 짧아 속도의 변화가 짧은 시간 안에 발생하므로 순간적인 속도 증분(\(\Delta V\))으로 근사할 수 있다.
\[ \int_{-\tau}^{+\tau} \begin{bmatrix} f_1(t) \\ f_2(t) \\ f_3(t) \end{bmatrix} dt = \begin{bmatrix} \Delta v_1 \\ \Delta v_2 \\ \Delta v_3 \end{bmatrix} \tag{10} \]
식 (9)에서 상수항과 상대 궤도요소의 관계는 다음과 같고 (https://pasus.tistory.com/240),
\[ \begin{align} & c_1=a \delta a, \ \ c_2=a \delta \lambda_0, \ \ c_3=a \delta e_x \tag{11} \\ \\ & c_4=a \delta e_y, \ \ c_5=a \delta i_x, \ \ c_6=a \delta i_y \end{align} \]
\(nt=u\) 에서 mean argument of latitude \(u\) 를 시간 대신 위치를 나타내는 독립 변수로 사용할 수 있으므로, 만약 초기 시간 \(t_0=0\) (또는 초기 위치 \(u_0=u_M\))에서 순간 추력을 사용한다면 식 (9)는 다음과 같이 쓸 수 있다.
\[ \Delta \begin{bmatrix} a \delta a \\ a \delta \lambda_0 \\ a \delta e_x \\ a \delta e_y \\ a \delta i_x \\ a \delta i_y \end{bmatrix} = \begin{bmatrix} 0 & \frac{2}{n} & 0 \\ -\frac{2}{n} & 0 & 0 \\ \frac{1}{n} \sin u_M & \frac{2}{n} \cos u_M & 0 \\ -\frac{1}{n} \cos u_M & \frac{2}{n} \sin u_M & 0 \\ 0 & 0 & \frac{1}{n} \cos u_M \\ 0 & 0 & \frac{1}{n} \sin u_M \end{bmatrix} \begin{bmatrix} \Delta v_1 \\ \Delta v_2 \\ \Delta v_3 \end{bmatrix} \tag{12} \]
식 (12)에 의하면 순간 추력은 상대 궤도요소의 순간적인 변화를 초래한다. 따라서 위성 편대의 대형 유지 또는 변경, 그리고 충돌회피를 위해 필요한 위치 \(u_M\) 과 필요한 상대 궤도요소의 변화를 알 수 있다면 식 (12)를 이용하여 필요한 속도 증분의 크기와 방향을 계산할 수 있다.
'항공우주 > 우주역학' 카테고리의 다른 글
| [CR3BP] 라그랑지 포인트 안정성 해석 (0) | 2023.06.22 |
|---|---|
| [CR3BP] 힐의 영역 (Hill’s Region) (0) | 2023.06.19 |
| 상대 궤도요소 (Relative Orbital Elements) - 2 (0) | 2023.02.07 |
| 상대 궤도요소 (Relative Orbital Elements) - 1 (0) | 2023.02.04 |
| CW 방정식 (Clohessy-Wiltshire Equations) (0) | 2023.01.27 |




댓글