상대 궤도요소 (Relative Orbital Elements) - 2

chief 위성의 궤도가 원궤도 또는 근 원궤도(near-circular orbit)일 경우, 시간 $t=t_0$ 에서 주어진 상대 궤도요소(ROM, relative orbital elements) $\delta \kappa$ 를 이용하면 Hill 좌표계에서 상대 위치벡터 $\delta \overrightarrow{r}=x{\hat{o}}_1+y{\hat{o}}_2+z{\hat{o}}_3$ 를 다음 식으로 표현할 수 있다 (https://pasus.tistory.com/240).

 

$$\begin{array}{r}\text{(1)}& x& \approx a\delta a-a\Vert \delta \overrightarrow{e}{\Vert }_2\cos (u-\phi )\\ y& \approx -\frac{3}{2}ua\delta a+a\delta {\lambda }_0+2a\Vert \delta \overrightarrow{e}{\Vert }_2\sin (u-\phi )\\ \\ z& \approx a\Vert \delta \overrightarrow{i}{\Vert }_2\sin (u-\vartheta )\end{array}$$

 

여기서 상대 궤도요소(ROM) $\delta \kappa$ 는 다음과 같다.

 

$$\begin{array}{r}\text{(2)}& \delta \kappa & =\left[\begin{array}{c}\delta a\\ \delta {\lambda }_0\\ \delta e_x\\ \delta e_y\\ \delta i_x\\ \delta i_y\end{array}\right]=\left[\begin{array}{c}\delta a\\ {\lambda }_0\\ \Vert \delta \overrightarrow{e}{\Vert }_2\cos \phi \\ \Vert \delta \overrightarrow{e}{\Vert }_2\sin \phi \\ \Vert \delta \overrightarrow{i}{\Vert }_2\cos \vartheta \\ \Vert \delta \overrightarrow{i}{\Vert }_2\sin \vartheta \end{array}\right]\\ & =\left[\begin{array}{c}\frac{a_d-a}{a}\\ (u_d(0)-u(0))+({\mathrm{\Omega }}_d-\mathrm{\Omega })\cos i\\ e_{x_d}-e_x\\ e_{y_d}-e_y\\ i_d-i\\ ({\mathrm{\Omega }}_d-\mathrm{\Omega })\sin i\end{array}\right]\end{array}$$

 

식 (1)에서 독립변수는 chief 위성의 mean argument of latitude인 $u=\omega +M$ 이다. 식 (1)과 (2)에서 $\delta a$ 와 $\delta {\lambda }_0$ 는 무차원화된 고전 궤도요소의 상대적인 차이를 나타내고 $\delta \overrightarrow{e}$ 와 $\delta \overrightarrow{i}$ 는 각각 상대 이심율 벡터(relative eccentricity vector)와 상대 경사각 벡터(relative inclination vector)를 나타낸다.

 

 

식 (2)로 주어지는 준 비특이(quasi-nonsingular) 상대 궤도요소(ROE)는 chief 위성과 deputy 위성간 상대 궤도의 기하학적 관계를 직관적으로 표현한다. 예를 들면, $\delta \overrightarrow{i}=0$ 인 경우 ${\hat{o}}_1-{\hat{o}}_3$ 평면(out-of-plane) 운동의 진폭이 $0$ 이라고 결론을 내릴 수 있다. 또한 $\delta a,\delta \lambda ,\delta \overrightarrow{e}$ 는 궤도면 운동을 나타내고 $\delta \overrightarrow{i}$ 는 궤도면 밖으로의 운동을 나타낸다. 이러한 장점 때문에 식 (2)로 주어지는 상대 궤도요소(ROE)는 군집 위성 운동에서 충돌회피(collision avoidance) 문제와 유도항법제어 설계 문제에 자주 사용되고 있다.

상대 궤도요소(ROE)를 Hill 좌표계의 ${\hat{o}}_1-{\hat{o}}_2$ 평면(in-plane)과 ${\hat{o}}_1-{\hat{o}}_3$ 평면(out-of-plane)에 나타내면 다음 그림과 같다.

 

 

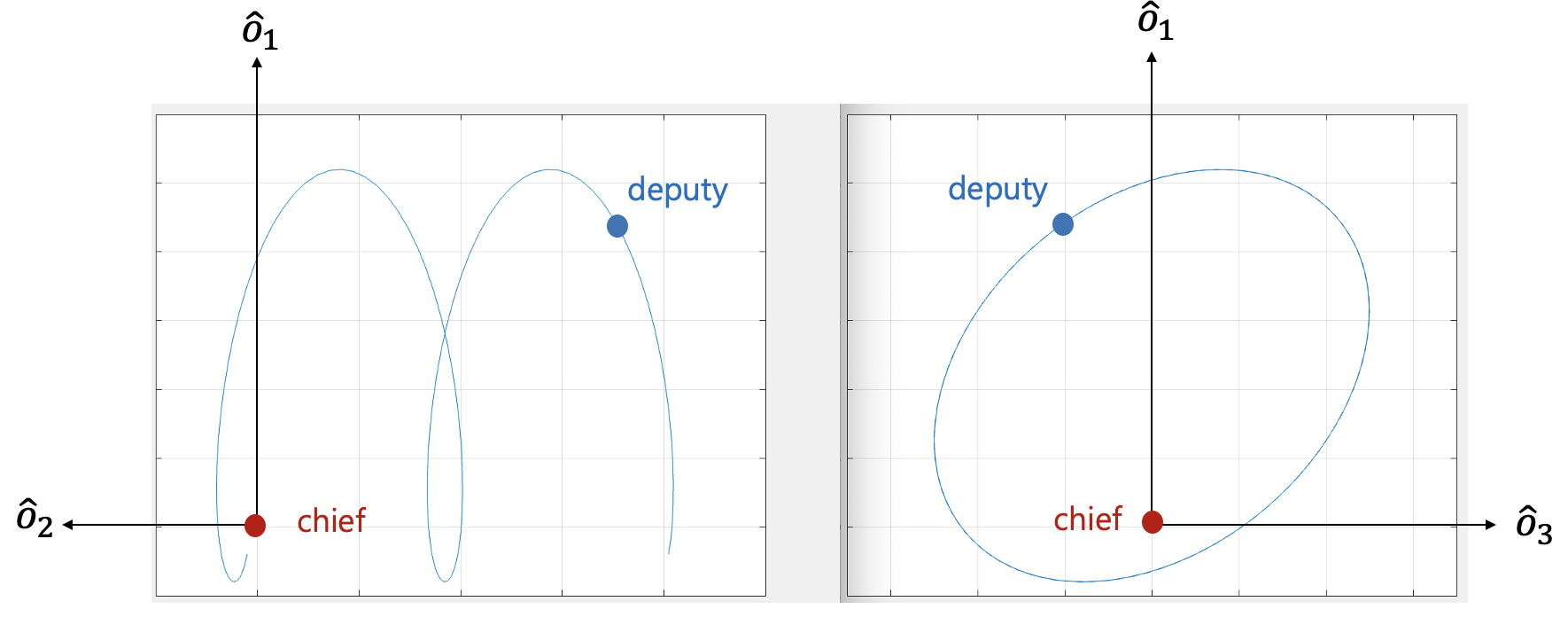
chief 위성과 deputy 위성 간의 ${\hat{o}}_2$ 축(along-track) 상의 거리가 계속 증가하는데 그 이유는 식 (1)에서 $\delta a$ 항 때문이다. 두 궤도 사이에서 $\delta a$ 가 $0$ 이 아닌 경우 궤도 주기가 다르기 때문에 두 궤도의 거리는 점차 멀어지게 된다. $\delta a=0$인 경우로 제한할 경우 Hill 좌표계의 ${\hat{o}}_1-{\hat{o}}_2$ 평면(in-plane)과 ${\hat{o}}_1-{\hat{o}}_3$ 평면(out-of-plane)에서 두 위성의 상대 운동을 나타내면 다음 그림과 같다.

 

 

$\delta a=0$ 의 조건이 적용될 때 chief 위성에 대한 deputy 위성의 상대 궤도는 ${\hat{o}}_2$ 축(along-track) 방향을 따라 장반경 $2a\Vert \delta \overrightarrow{e}{\Vert }_2$ 및 ${\hat{o}}_1$ 축(반경) 방향으로 단반경 $a\Vert \delta \overrightarrow{e}{\Vert }_2$ 인 타원이 된다. $a\delta {\lambda }_0$ 는 ${\hat{o}}_2$ 축(along-track) 방향으로의 타원 중심까지의 거리를 나타내고 $\Vert \delta \overrightarrow{e}{\Vert }_2$ 는 ${\hat{o}}_1-{\hat{o}}_2$ 평면(궤도면)에서의 진동 크기를 나타낸다. mean argument of latitude인 $u$ 가 위상각 $\phi$ 와 값이 같을 때에는 deputy 위성은 타원 중심 바로 아래에 위치하고 $u=\phi +\frac{\pi }{2}$ 이면 chief 위성의 바로 앞에 위치한다.

상대 경사각 벡터 $\delta \overrightarrow{i}$ 는 궤도면에 수직인 상대 운동을 설명하는 데 사용된다. ${\hat{o}}_1-{\hat{o}}_3$ 평면(out-of-plane)에서의 상대 궤도는 기울어진 타원이며 위상각의 차이인 $\phi -\vartheta$ 는 기울어진 타원의 방향과 관련이 있다. chief 위성에 대한 deputy 위성의 상대 운동은 진폭 $a\Vert \delta \overrightarrow{i}{\Vert }_2$ 및 위상각 $u-\vartheta$ 의 조화 진동 운동이다.

상대 경사각 벡터 $\delta \overrightarrow{i}$ 는 정의만 보면 기하학적으로 어떤 값을 의미하는지 모호할 수 있다. 이에 대한 보다 구체적인 이해를 위하여 다음 그림을 보자.

 

 

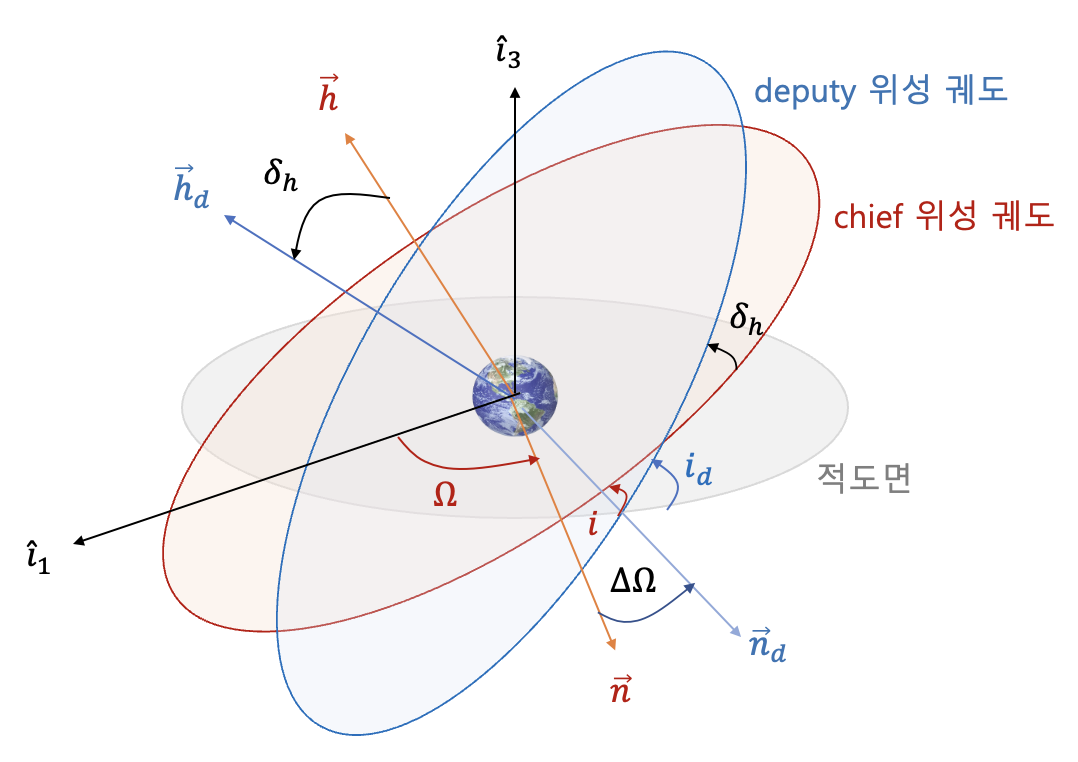
그림에서 $\overrightarrow{h}$ 는 chief 위성의 각운동력 벡터, ${\overrightarrow{h}}_d$ 는 deputy 위성의 각운동력 벡터이다. 두 각운동량 벡터의 사이각 ${\delta }_h$ 는 두 궤도의 경사각의 차이 $\mathrm{\Delta }=i=i_d-i$ 뿐만 아니라 RAAN의 차이 $\mathrm{\Delta }\mathrm{\Omega }={\mathrm{\Omega }}_d-\mathrm{\Omega }$ 의 함수이기도 한데, 그 관계식은 다음과 같이 주어진다.

 

$$\begin{array}{r}\text{(3)}& \cos {\delta }_h& =\cos i\cos i_d+\sin i\sin i_d\cos \mathrm{\Delta }\mathrm{\Omega }\\ & =\cos i\cos (i+\mathrm{\Delta }i)+\sin i\sin (i+\mathrm{\Delta }i)\cos \mathrm{\Delta }\mathrm{\Omega }\end{array}$$

 

만약 $\mathrm{\Delta }i,\mathrm{\Delta }\mathrm{\Omega },{\delta }_h$ 가 작은 값이라면 위 식은 다음과 같이 근사화할 수 있다.

 

$$\begin{array}{r}\text{(4)}& 1-\frac{{\delta }_h^2}{2}& \approx {\cos }^{2}i(1-\frac{\mathrm{\Delta }{i}^2}{2})-\cos i\sin i\mathrm{\Delta }i\\ & +({\sin }^{2}i(1-\frac{\mathrm{\Delta }{i}^2}{2})+\sin i\cos i\mathrm{\Delta }i)(1-\frac{\mathrm{\Delta }{\mathrm{\Omega }}^2}{2})\\ \\ & =1-\frac{\mathrm{\Delta }{i}^2}{2}-(1-\frac{\mathrm{\Delta }{i}^2}{2}){\sin }^{2}i\frac{\mathrm{\Delta }{\mathrm{\Omega }}^2}{2}-\sin i\cos i\mathrm{\Delta }i\frac{\mathrm{\Delta }{\mathrm{\Omega }}^2}{2}\\ \\ & \approx 1-\frac{\mathrm{\Delta }{i}^2}{2}-{\sin }^{2}i\frac{\mathrm{\Delta }{\mathrm{\Omega }}^2}{2}\end{array}$$

 

따라서

 

$$\begin{array}{}\text{(5)}& {\delta }_h\approx \sqrt{\mathrm{\Delta }{i}^2+{\sin }^{2}i\mathrm{\Delta }{\mathrm{\Omega }}^2}\end{array}$$

 

이 된다. 상대 경사각 벡터(relative inclination vector)의 정의와 비교해 보면 ${\delta }_h$ 는 $\Vert \delta \overrightarrow{i}{\Vert }_2$ 와 같다는 것을 알 수 있다. 따라서 $\Vert \delta \overrightarrow{i}{\Vert }_2$ 는 chief 궤도면에 대한 deputy 궤도면의 기울어진 각을 의미한다.