[CR3BP] L1, L2 및 L3 포인트에서의 궤도 운동

CR3BP의 선형화된 운동방정식을 이용하여 라그랑지 포인트(Lagrange point) L4 및 L5 포인트는 (중립) 안정 평형점이지만, L1, L2 및 L3 포인트는 불안정한 평형점이라는 것을 확인했다 (https://pasus.tistory.com/271).

 

 

하지만 L1, L2 및 L3 포인트의 고유값(eigenvalue) 분석에 의하면 평형점 주위에 주기 궤도(periodic orbit)가 존재함을 시사한다. 즉 특정한 초기조건을 설정하면 불안정한 운동 모드를 배제하고 주기 운동을 하는 모드만을 나타나게 할 수가 있다.

 

 

라그랑지 포인트에서의 선형화 운동방정식은 다음과 같다.

 

$$\begin{array}{r}\text{(1)}& & \delta \ddot{x}-2\delta \dot{y}=-{\overline{U}}_{xx}\delta x-{\overline{U}}_{xy}\delta y\\ & \delta \ddot{y}+2\delta \dot{x}=-{\overline{U}}_{xy}\delta x-{\overline{U}}_{yy}\delta y\\ \\ & \delta \ddot{z}=-{\overline{U}}_{zz}\delta z\end{array}$$

 

L1, L2 및 L3 포인트에서는 ${\overline{U}}_{xx},{\overline{U}}_{xy},{\overline{U}}_{yy},{\overline{U}}_{zz}$ 가 각각 다음과 같이 계산된다.

 

$$\begin{array}{r}\text{(2)}& & {\overline{U}}_{xx}=-1-2c_2\\ & {\overline{U}}_{yy}=-1+c_2\\ \\ & {\overline{U}}_{xy}=0\\ \\ & {\overline{U}}_{zz}=c_2\\ \\ & c_2=\frac{(1-\mu )}{|x_0+\mu {|}^3}+\frac{\mu }{(|x_0+\mu -1{|}^3}\end{array}$$

 

식 (2)를 식 (1)에 대입하면 다음과 같이 된다.

 

$$\begin{array}{r}\text{(3)}& & \delta \ddot{x}-2\delta \dot{y}-(1+2c_2)\delta x=0\\ & \delta \ddot{y}+2\delta \dot{x}+(-1+c_2)\delta y=0\\ \\ & \delta \ddot{z}+c_2\delta z=0\end{array}$$

 

여기서 $c_2>1$ 이다. 식 (3)에서 $\delta z$ 방정식은 $\delta x,\delta y$ 방정식과 독립적이므로 별도로 계산할 수 있다.

 

$$\begin{array}{}\text{(4)}& \delta z(t)=A_z\sin ({\omega }_{v}t+\psi )\end{array}$$

 

여기서 ${\omega }_v^2=c_2$ 이다. $A_z$ 와 $\psi$ 는 섭동량 $\delta z$ 의 초기조건에 의해서 결정되는 상수이다.

식 (3)에서 $\delta x,\delta y$ 운동은 결합되어 있기 때문에 다음과 같이 벡터 형식으로 바꾸는 것이 편리하다.

 

$$\begin{array}{}\text{(5)}& \dot{\mathbf{w}}=A\mathbf{w}\end{array}$$

여기서

$$A=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ (1+2c_2)& 0& 0& 2\\ 0& (1-c_2)& -2& 0\end{array}\right],\mathbf{w}=\left[\begin{array}{c}\delta x\\ \delta y\\ \delta v_x\\ \delta v_y\end{array}\right]$$

 

식 (5)에서 행렬 $A$ 의 고유값을 구해보자. 먼저 특성방정식은 다음과 같으므로

 

$$\begin{array}{r}\text{(6)}& det(A-\lambda I)& =det\left[\begin{array}{cccc}-\lambda & 0& 1& 0\\ 0& -\lambda & 0& 1\\ (1+2c_2)& 0& -\lambda & 2\\ 0& (1-c_2)& -2& -\lambda \end{array}\right]\\ & ={\lambda }^4+(2-c_2){\lambda }^2+(1+c_2-2c_2^2)\\ \\ & =0\end{array}$$

 

고유값은 다음과 같다.

 

$$\begin{array}{r}\text{(7)}& & {\lambda }_1^2=\frac{c_2-2+\sqrt{9c_2^2-8c_2}}{2}>0\\ & {\lambda }_3^2=\frac{c_2-2-\sqrt{9c_2^2-8c_2}}{2}<0\end{array}$$

 

식 (7)에 의하면 행렬 $A$ 의 고유값은 두개의 실수 ${\lambda }_{1,2}=\pm \lambda$ 와 두개의 허수 ${\lambda }_{3,4}=\pm j{\omega }_p$ 를 갖는다. 각 고유값에 해당하는 고유벡터(eigenvector)를 구하기 위하여 고유값 $\alpha$ 에 해당하는 고유벡터를 $\mathbf{v}=[v_1{v}_2{v}_3{v}_4{]}^T$ 라고 하자. 그러면 다음식이 성립한다.

 

$$\begin{array}{}\text{(8)}& \left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ (1+2c_2)& 0& 0& 2\\ 0& (1-c_2)& -2& 0\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]=\alpha \left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]\end{array}$$

 

위 식을 전개하면 다음과 같은 관계식을 갖는다.

 

$$\begin{array}{r}\text{(9)}& & v_3=\alpha v_1,v_4=\alpha v_2\\ & (1+2c_2)v_1+2v_4=\alpha v_3,(1-c_2)v_2-2v_3=\alpha v_4\end{array}$$

 

만약 $v_1=0$ 이면 $v_2=v_3=v_4=0$ 이 되므로 $v_1\ne 0$ 이어야 한다. $v_1=1$ 로 놓으면 식 (9)에 의해서 고유벡터는 다음과 같이 된다.

 

$$\begin{array}{}\text{(10)}& \mathbf{v}=\left[\begin{array}{c}1\\ v_2\\ \alpha \\ \alpha v_2\end{array}\right]\end{array}$$

 

이제 고유값이 $\pm \lambda$ 일 때 고유벡터 ${\mathbf{v}}_1,{\mathbf{v}}_2$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(11)}& {\mathbf{v}}_1=\left[\begin{array}{c}1\\ v_2\\ \lambda \\ \lambda v_2\end{array}\right],{\mathbf{v}}_2=\left[\begin{array}{c}1\\ v_2^{\prime }\\ -\lambda \\ -\lambda v_2^{\prime }\end{array}\right]\end{array}$$

여기서

 

$$\begin{array}{rl}& (1+2c_2)+2\lambda v_2={\lambda }^2,(1-c_2)v_2-2\lambda ={\lambda }^2{v}_2\\ \\ & (1+2c_2)-2\lambda v_2^{\prime }={\lambda }^2,(1-c_2)v_2^{\prime }+2\lambda ={\lambda }^2{v}_2^{\prime }\end{array}$$

 

이므로 $v_2=-v_2^{\prime }$ 임을 알 수 있다. 따라서

 

$$\begin{array}{}\text{(12)}& v_2=-v_2^{\prime }=\frac{-2\lambda }{{\lambda }^2+c_2-1}=\frac{{\lambda }^2-(1+2c_2)}{2\lambda }\end{array}$$

 

이다. 식 (12)를 식 (11)에 대입하면 고유값이 $\pm \lambda$ 일 때 고유벡터 ${\mathbf{v}}_1,{\mathbf{v}}_2$ 는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(13)}& {\mathbf{v}}_1=\left[\begin{array}{c}1\\ v_2\\ \lambda \\ \lambda v_2\end{array}\right],{\mathbf{v}}_2=\left[\begin{array}{c}1\\ -v_2\\ -\lambda \\ \lambda v_2\end{array}\right]\end{array}$$

 

 

 

한편 고유값이 $\pm j{\omega }_p$ 일 때 고유벡터 ${\mathbf{v}}_3,{\mathbf{v}}_4$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(14)}& {\mathbf{v}}_3=\left[\begin{array}{c}1\\ v_2^{″}\\ j{\omega }_p\\ j{\omega }_p{v}_2^{″}\end{array}\right],{\mathbf{v}}_4=\left[\begin{array}{c}1\\ v_2^{‴}\\ -j{\omega }_p\\ -j{\omega }_p{v}_2^{‴}\end{array}\right]\end{array}$$

여기서

 

$$\begin{array}{rl}& (1+2c_2)+2j{\omega }_p{v}_2^{″}=-{\omega }_p^2,(1-c_2)v_2^{″}+2j{\omega }_p=-{\omega }_p^2{v}_2^{″}\\ \\ & (1+2c_2)-2j{\omega }_p{v}_2^{‴}=-{\omega }_p^2,(1-c_2)v_2^{‴}-2j{\omega }_p=-{\omega }_p^2{v}_2^{‴}\end{array}$$

 

이므로 $v_2^{″}=-v_2^{‴}$ 임을 알 수 있다. 따라서

 

$$\begin{array}{}\text{(15)}& v_2^{″}=-v_2^{‴}=-j\frac{2{\omega }_p}{{\omega }_p^2-c_2+1}=j\frac{{\omega }_p^2+(1+2c_2)}{2{\omega }_p}=j\kappa \end{array}$$

 

이다. 식 (15)를 식 (14)에 대입하면 고유값이 $\pm j{\omega }_p$ 일 때 고유벡터 ${\mathbf{v}}_3,{\mathbf{v}}_4$ 는 다음과 같이 쓸 수 있다.

 

$$\begin{array}{r}\text{(16)}& & {\mathbf{v}}_3=\left[\begin{array}{c}1\\ j\kappa \\ j{\omega }_p\\ -{\omega }_p\kappa \end{array}\right]=\left[\begin{array}{c}1\\ 0\\ 0\\ -{\omega }_p\kappa \end{array}\right]+j\left[\begin{array}{c}0\\ \kappa \\ {\omega }_p\\ 0\end{array}\right]={\mathbf{v}}_R+j{\mathbf{v}}_I\\ & {\mathbf{v}}_4=\left[\begin{array}{c}1\\ -j\kappa \\ -j{\omega }_p\\ -{\omega }_p\kappa \end{array}\right]=\left[\begin{array}{c}1\\ 0\\ 0\\ -{\omega }_p\kappa \end{array}\right]-j\left[\begin{array}{c}0\\ \kappa \\ {\omega }_p\\ 0\end{array}\right]={\mathbf{v}}_R-j{\mathbf{v}}_I\end{array}$$

 

실수 고유값에 해당하는 고유벡터 ${\mathbf{v}}_1,{\mathbf{v}}_2$ 는 각각 안정 부분공간(stable subspace)과 불안정 부분공간의 기저벡터, 허수 고유값에 해당하는 고유벡터 ${\mathbf{v}}_R,{\mathbf{v}}_I$ 는 센터(center) 부분공간의 기저벡터이다.

각 부분공간의 고유벡터로 변환행렬 $T$ 를 다음과 같이 정의하면

 

$$\begin{array}{}\text{(17)}& T=\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& {\mathbf{v}}_R& {\mathbf{v}}_I\end{array}\right]\end{array}$$

 

식 (1)의 상태벡터 $\mathbf{w}$ 를 다음과 같이 상태벡터 $\mathbf{a}$ 로 변환할 수 있다 (https://pasus.tistory.com/233).

 

$$\begin{array}{r}\text{(18)}& & \dot{\mathbf{a}}=T^{-1}AT\mathbf{a}=D\mathbf{a}\\ \to & \left[\begin{array}{c}{\dot{a}}_1\\ {\dot{a}}_2\\ {\dot{a}}_3\\ {\dot{a}}_4\end{array}\right]=\left[\begin{array}{cccc}\lambda & 0& 0& 0\\ 0& -\lambda & 0& 0\\ 0& 0& 0& {\omega }_p\\ 0& 0& -{\omega }_p& 0\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\\ a_4\end{array}\right]\end{array}$$

 

식 (18)로 주어지는 $\mathbf{a}$ 의 해는 다음과 같다.

 

$$\begin{array}{r}\text{(19)}& & a_1(t)=a_{10}{e}^{\lambda t}\\ & a_2(t)=a_{20}{e}^{-\lambda t}\\ \\ & a_3(t)=a_{30}\cos {\omega }_{p}t+a_{40}\sin {\omega }_{p}t\\ \\ & a_4(t)=-a_{30}\sin {\omega }_{p}t+a_{40}\cos {\omega }_{p}t\end{array}$$

 

여기서 $a_{10},a_{20},a_{30},a_{40}$ 은 초기값이다. 식 (19)에 의하면 라그랑지 포인트에 대한 선형 운동을 $(a_1-a_2)$ 좌표로 투사시키면 L1, L2, L3 포인트는 안장점(saddle point)이 되고, $(a_3-a_4)$ 좌표로 투사시키면 중심점(center point)이 됨을 알 수 있다. 그래서 L1, L2, L3 포인트를 안장-중심 평형점(saddle-center equilibrium point)이라고 하기도 한다.

 

 

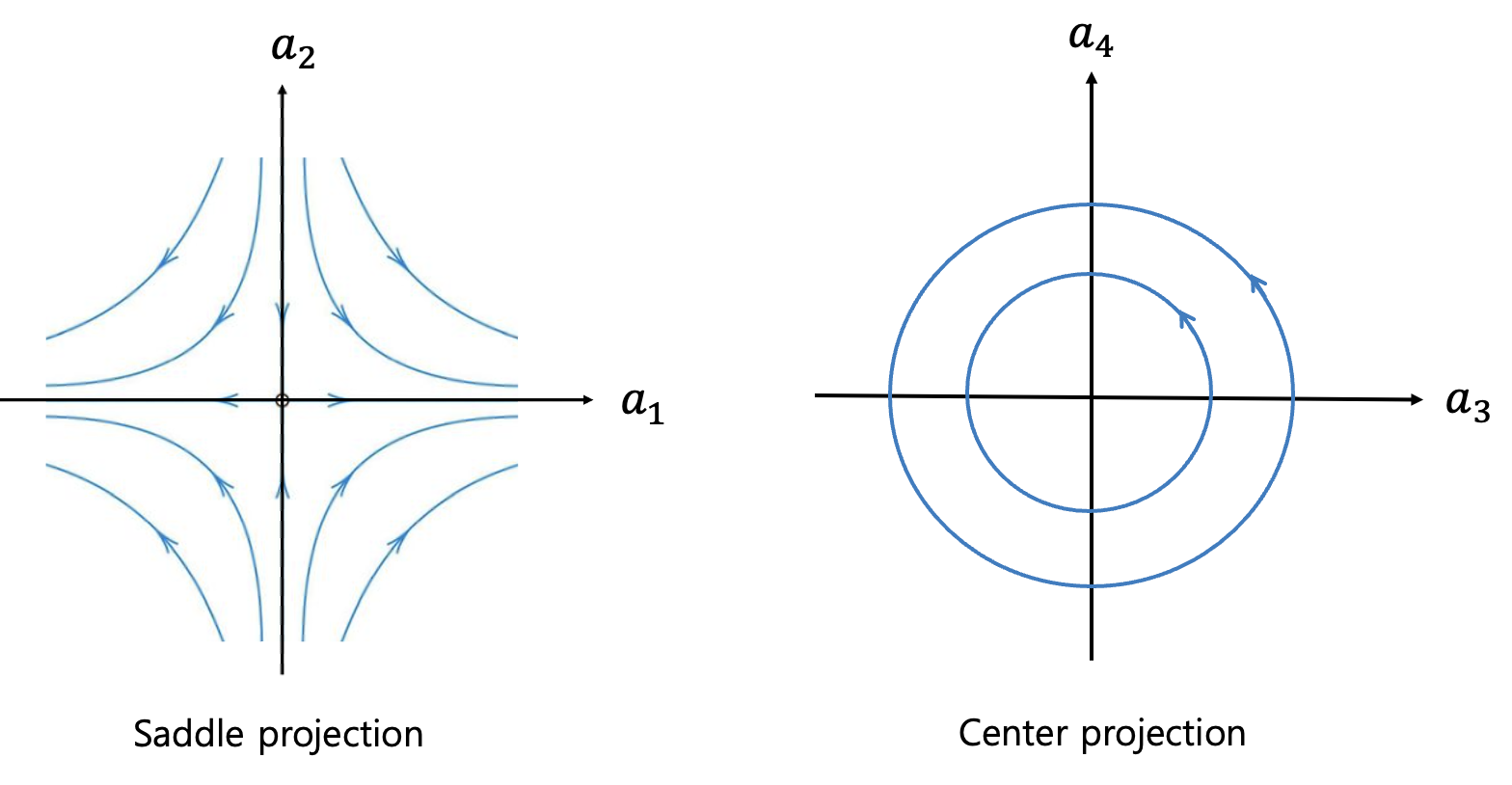
또한 식 (19)에 의하면 초기값을 불안정 운동을 배제하도록 잘 설정한다면, 즉 $a_1=a_2=0$ 이 된다면 라그랑지 포인트를 중심으로 하는 주기 궤도(periodic orbit) 운동이 가능함을 알 수 있다. 그리고 L1, L2, L3 포인트에 대한 선형화 운동은 전체적으로 불안정하지만 $a_{10}=0$ 이면 궤도 운동이 안정할 수 있다는 것을 알 수 있다.

 

 

추가적으로 안장점 투사 그림에 의하면 라그랑지 포인트 주변 영역을 통과(transit)하는 궤도와 통과하지 않는 비통과(non-transit) 궤도도 존재함을 알 수 있다.