어떤 유동장에서 운동하는 미소 유체요소(infinitesimal fluid element)를 생각해보자.
아래 그림과 같이 이 유체요소는 운동하면서 회전할 수도 있고 모양이 변할 수도 있다. 이 회전 및 모양의 변화 정도는 유체의 속도장에 따라 다르다. 여기서는 유체요소의 회전에 집중하여 유체의 속도장과 유체요소의 회전 각속도(angular velocity)의 관계에 대해서 알아보고자 한다.

논의를 간단하게 하기 위해서 일단 유체가 2차원 평면상을 흐른다고 하자. 아래 그림과 같이 시간 \(t\) 에서 이 유체요소의 모양이 직사각형이라고 가정한다. 시간이 \(\Delta t\) 만큼 흐르면 유체요소의 꼭지점 B와 C는 꼭지점 A에 대해서 각각 상대 위치가 변화한다. 유체요소의 각 점의 상대 속도가 그림에 표시된 대로 차이가 나기 때문이다. 그러면 유체요소의 위치와 모양은 변화하게 된다.
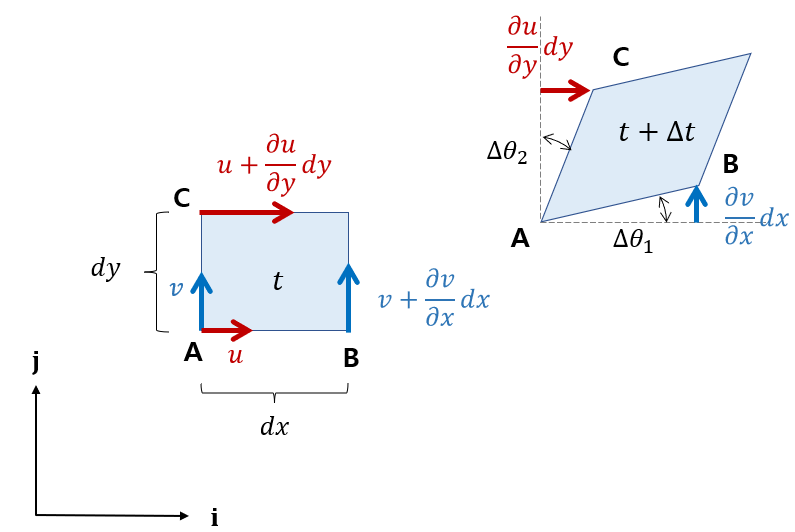
먼저 y 축 방향의 속도 변화에 의한 유체요소의 변위를 계산해 보자. 시간 \(t\) 에서 점 A의 y축 방향 속도 성분은 \(v\) 이다. 점 B는 점 A로부터 거리 \(dx\) 만큼 떨어져 있으므로 속도 성분은 \(v+ \frac{\partial v}{ \partial x} dx \) 로 주어진다. 따라서 점 B와 A의 y축 방향 상대 변위는 다음과 같다.
\[ \left( v+ \frac{\partial v}{\partial x} dx \right) \Delta t -v \Delta t = \frac{\partial v}{\partial x} dx \Delta t \tag{1} \]
점 B는 점 A를 기준으로 상대적으로 \(\Delta \theta_1\) 만큼 회전한 것으로 볼 수 있다.
\[ \tan \Delta \theta_1 \approx \Delta \theta_1= \frac{ \frac{\partial v}{\partial x} dx \Delta t }{dx} = \frac{\partial v}{\partial x} \Delta t \tag{2} \]
점 C와 A의 x축 방향 상대 변위도 비슷한 방법으로 구하면 다음과 같다.
\[ \left( u+ \frac{\partial u}{\partial y} dy \right) \Delta t - u \Delta t = \frac{\partial u}{\partial y} dy \Delta t \tag{3} \]
여기서 \(u\) 는 x축 방향 속도 성분이다. 점 C는 점 A를 기준으로 상대적으로 \(- \Delta \theta_2\) 만큼 회전한 것으로 볼 수 있다.
\[ \tan (-\Delta \theta_2) \approx -\Delta \theta_2 = \frac{ \frac{\partial u}{\partial y} dy \Delta t }{dy} = \frac{\partial u}{\partial y} \Delta t \tag{4} \]
여기서 \(-\)(마이너스) 부호가 붙은 이유는 반시계 방향 회전을 \(+\)(플러스) 방향으로 보기 때문이다. 식 (2)와 (4)에 의하면 유체요소의 변 AB와 AC의 각 변화율을 계산할 수 있다.
\[ \begin{align} & \frac{d \theta_1}{dt}= \lim_{\Delta t \to 0} \frac{\Delta \theta_1 }{\Delta t} = \frac{\partial v}{\partial x} \tag{5} \\ \\ & \frac{d \theta_2}{dt}= \lim_{\Delta t \to 0} \frac{\Delta \theta_2 }{\Delta t} = -\frac{\partial u}{\partial y} \end{align} \]
xy 평면에서 유체요소의 각속도 \( \Omega_z \) 는 정의에 의해서 변 AB와 AC의 각속도의 평균으로 주어진다.
\[ \Omega_z= \frac{1}{2} \left( \frac{d \theta_1}{dt} + \frac{d \theta_2}{dt} \right) =\frac{1}{2} \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \tag{6} \]
비슷한 방법으로 yz, xz 평면에서도 유체요소의 각속도 성분을 계산하면, 3차원 공간에서 유체요소의 각속도 벡터 \( \mathbf{\Omega}\)를 다음과 같이 구할 수 있다.
\[ \begin{align} \mathbf{\Omega} &= \Omega_x \mathbf{i} + \Omega_y \mathbf{j} + \Omega_z \mathbf{k} \tag{7} \\ \\ &= \frac{1}{2} \left[ \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right) \mathbf{i} + \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right) \mathbf{j} + \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \mathbf{k} \right] \end{align} \]
여기서 \(w\) 는 z축 방향 속도 성분이다.
식 (7)로 주어지는 유체요소 각속도 벡터의 두 배를 Vorticity (보통 와도라고 변역한다) \(\mathbf{\omega}\) 로 정의한다.
\[ \mathbf{\omega} = 2 \mathbf{\Omega} = \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right) \mathbf{i} + \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right) \mathbf{j} + \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \mathbf{k} \tag{8} \]
Curl의 정의를 이용하면 Vorticity 정의 식 (8)을 다음과 같이 쓸 수 있다.
\[ \mathbf{\omega} = \nabla \times \mathbf{V} \tag{9} \]
이와 같은 정의에 의하면 Vorticity는 미소 유체요소가 운동하면서 회전하는 정도를 표현한 벡터량이다.
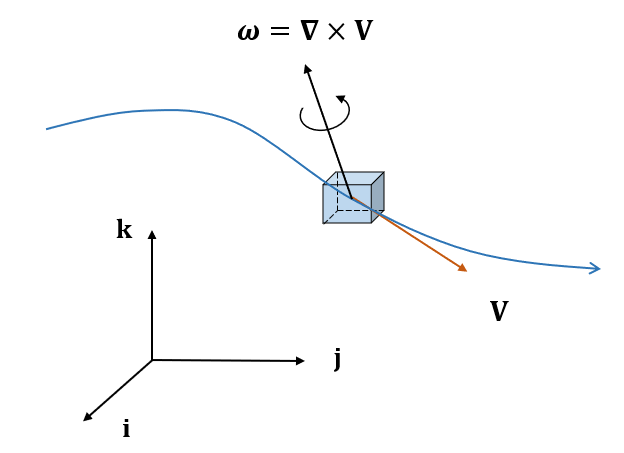
유동장의 모든 지점에서 \(\nabla \times \mathbf{V} \ne 0\) 이라면 그 유체의 흐름을 회전류 (rotational flow)라고 하고 \(\nabla \times \mathbf{V} = 0\) 이면 비회전류 (irrotational flow)라고 한다.
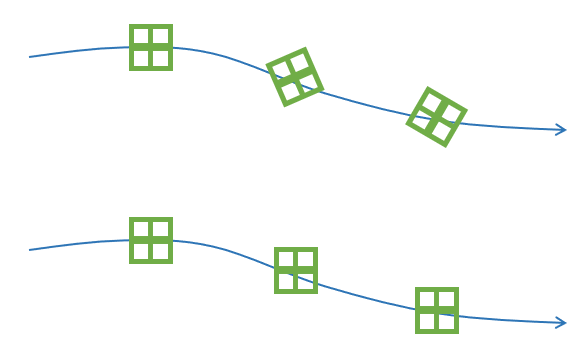
다음 그림은 회전류와 비회전류를 보여준다. 구분은 유체요소가 자전하는지 안하는지에 달려있다.
'항공우주 > 항공역학' 카테고리의 다른 글
| 이류(advection), 대류(convection), 확산(diffusion) (0) | 2023.10.07 |
|---|---|
| Vorticity 미분 방정식 (0) | 2022.05.29 |
| 유동장의 시간미분에 대해서 (0) | 2022.05.24 |
| Navier-Stokes 방정식의 벡터 표현 (0) | 2021.10.22 |
| Navier-Stokes 방정식 - 2 (0) | 2021.08.10 |




댓글