미사일의 속도 \(\vec{V}\) 는 ECEF 기준, 즉 지면 기준의 상대적인 속도이므로 다음과 같다.
\[ \vec{V} = \frac{^ed\vec{r}}{dt} \tag{1} \]
여기서 \(\vec{r}\) 는 지구 중심에서 미사일까지의 위치벡터다.
한편 미사일의 질량 중심점을 원점으로 하고 속도 방향을 x축, 지표면과 수평인 평면에서 속도 방향의 오른쪽 방향을 y축으로 하는 좌표계를 미사일 운동 좌표계 \(\{d\}\) 로 정의하므로 속도벡터를 좌표계 \(\{d\}\) 로 표시하면 다음과 같다.
\[ V^d= \begin{bmatrix} V \\ 0 \\ 0 \end{bmatrix} \tag{2} \]
여기서 \(V\) 는 \(\vec{V}\) 의 크기다.
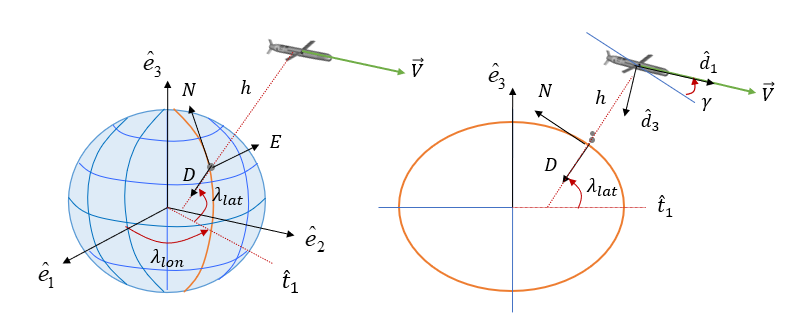
NED(North-East-Down) 좌표계 \(\{n\}\) 에서 미사일의 속도를 표현하기 위해서는 좌표계 \(\{d\}\) 와 \(\{n\}\) 간의 DCM(방향코사인행렬) \(C_d^n\) 를 이용하면 된다.
\[ \begin{align} V^n &= C_d^n V^d=C(z, \psi) C(y, \gamma) V^d \tag{3} \\ \\ &= \begin{bmatrix} V \cos \psi \cos \gamma \\ V \cos \psi \sin \gamma \\ -V \sin \gamma \end{bmatrix} \end{align} \]
여기서 \(\psi\) 는 북쪽 방향을 기준으로 측정한 속도벡터의 방위각이며 \(\gamma\) 는 비행경로각으로서 수평면과 미사일 속도벡터가 이루는 각이다. 또한 좌표계 \(\{n\}\) 과 ECEF 좌표계 \(\{e\}\) 간의 DCM \(C_e^n\) 를 이용하여 미사일 속도를 다음과 같이NED 좌표계로 표현할 수도 있다.
\[ \begin{align} V^n &= C_e^n \dot{r}^e \tag{4} \\ \\ &=(C_n^e )^T \dot{r}^e \\ \\ &=C(y, \pi/2 + \lambda_{lat} ) C(z ,-\lambda_{lon} ) \dot{r}^e \end{align} \]
여기서 \(\lambda_{lat}\) 는 미사일 위치의 위도, \(\lambda_{lon}\) 는 경도, \(\dot{r}^e\) 는 \(\frac{^e d\vec{r}}{dt}\) 를 ECEF 좌표계로 표현한 벡터이다.

ECEF 좌표계로 표현된 미사일의 위치를 위도, 경도, 높이(LLH, Latitude-Longitude-Height) 좌표계로 나타내면 다음과 같다.
\[ r^e= \begin{bmatrix} (R_{tr}+h) \cos \lambda_{lat} \cos \lambda_{lon} \\ (R_{tr}+h) \cos \lambda_{lat} \sin \lambda_{lon} \\ \left( R_{tr} (1-e_{er}^2 )+h \right) \sin \lambda_{lat} \end{bmatrix} \tag{5} \]
여기서 \(r^e\) 은 미사일의 위치를 ECEF 좌표계로 표현한 벡터이며, \(e_{er}\) 는 지구 이심율, \(h\) 는 지면에서의 고도이고, \(R_{tr}\) 는 접선 반경(tangential radius)으로서
\[ R_{tr} = \frac{R_{eq}}{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat}}} \tag{6} \]
이다. 여기서 \(R_{eq}\) 는 지구 적도 반지름이다.
식 (3)과 (4)는 모두 미사일의 속도를 NED 좌표계로 표현한 식이므로 서로 같아야 한다. 따라서 다음 식이 성립한다.
\[ \begin{bmatrix} V \cos \psi \cos \gamma \\ V \cos \psi \sin \gamma \\ -V \sin \gamma \end{bmatrix} = \begin{bmatrix} -\sin \lambda_{lat} \cos \lambda_{lon} & -\sin \lambda_{lat} \sin \lambda_{lon} & \cos \lambda_{lat} \\ -\sin \lambda_{lon} & \cos \lambda_{lon} & 0 \\ -\cos \lambda_{lat} \cos \lambda_{lon} & -\cos \lambda_{lat} \sin \lambda_{lon} & -\sin \lambda_{lat} \end{bmatrix} \dot{r}^e \tag{7} \]
위 식에서 \(\dot{r}^e\) 는 식 (5)를 미분하면 구할 수 있다.
\[ \dot{r}^e= \begin{bmatrix} (\dot{R}_{tr}+\dot{h}) c \lambda_{lat} c \lambda_{lon} - \dot{\lambda}_{lat} (R_{tr}+h) s \lambda_{lat} c \lambda_{lon} - \dot{\lambda}_{lon} (R_{tr}+h) c \lambda_{lat} s \lambda_{lon} \\ (\dot{R}_{tr}+ \dot{h}) c \lambda_{lat} s \lambda_{lon} - \dot{\lambda}_{lat} (R_{tr}+h) s \lambda_{lat} s \lambda_{lon} + \dot{\lambda}_{lon} (R_{tr}+h) c \lambda_{lat} c \lambda_{lon} \\ \left( \dot{R}_{tr} (1-e_{er}^2 )+ \dot{h} \right) s \lambda_{lat} + \dot{\lambda}_{lat} \left( R_{tr} (1-e_{er}^2 )+h \right) c \lambda_{lat} \end{bmatrix} \tag{8} \]
식 (8)에서 \(\dot{R}_{tr}\) 는 식 (6)을 미분하면 구할 수 있다.
\[ \dot{R}_{tr} = \dot{\lambda}_{lat} \frac{ R_{eq} e_{er}^2 \sin \lambda_{lat} \cos \lambda_{lat} }{ (1-e_{er}^2 \sin^2 \lambda_{lat} )^ {3/2} } \tag{9} \]
식 (8), (9)를 식 (7)에 대입하면 다음과 같은 식이 얻어진다.
\[ \begin{bmatrix} V \cos \psi \cos \gamma \\ V \cos \psi \sin \gamma \\ -V \sin \gamma \end{bmatrix} = \begin{bmatrix} \dot{\lambda}_{lat} (R_{mr}+h) \\ \dot{\lambda}_{lon} (R_{tr}+h) \cos \lambda_{lat} \\ -\dot{h} \end{bmatrix} \tag{10} \]
여기서 \(R_{mr}\) 은 자오선 반경(meridian radius)으로서
\[ R_{mr} = \frac{ R_{eq} (1-e_{er}^2) }{ (1-e_{er}^2 \sin^2 \lambda_{lat} )^{3/2} } \tag{11} \]
이다. 식 (10)으로부터 다음과 같이 미사일 속도와 위도, 경도, 높이의 변화율 관계식을 얻을 수 있다.
\[ \begin{align} & \dot{\lambda}_{lat}= \frac{ V \cos \psi \cos \gamma}{ R_{mr}+h} \tag{12} \\ \\ & \dot{\lambda}_{lon}= \frac{ V \sin \psi \cos \gamma }{ (R_{tr}+h) \cos \lambda_{lat}} \\ \\ & \dot{h}=V \sin \gamma \end{align} \]
기하학적인 방법으로 식 (12)를 계산할 수도 있다. 이 방법도 계산 과정은 복잡하지만 개념적으로는 더 이해하기가 쉽다.
자오선은 북극과 남극에서 교차하므로 특정 경도 변화에 해당하는 거리는 위도에 따라 다르다. 위도가 높을수록 동일한 경도의 변화에 따른 거리가 더 짧아진다. 한편, 지구는 자오선을 기준으로 자른 단면이 타원형이므로 위도의 변화에 해당하는 거리도 위도에 따라 달라진다.
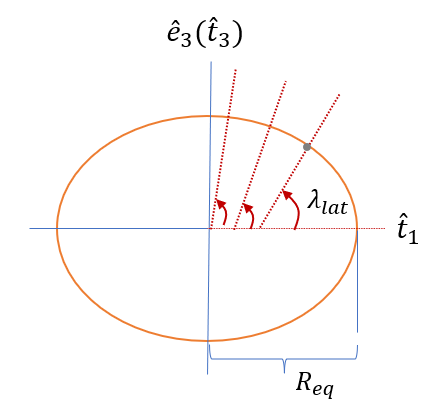
먼저 특정 위도에서 경도 변화에 따른 지구 표면의 거리의 변화를 계산해 보자. 지구의 적도에 대한 모든 평행선은 일정한 반지름을 갖는 원이다. 위도 \(\lambda_{lat}\) 에서 아래 그림의 \(D\) 는 경도의 미소 변화 \(d \lambda_{lon}\) 에 대한 지구 표면의 미소 거리 \(ds_{lon}\) 를 결정하기 위한 반지름이다.
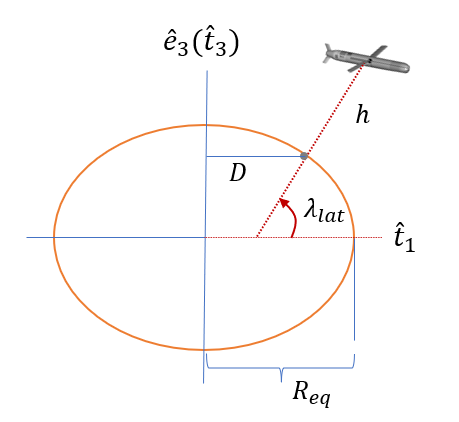
\(D\) 는 다음과 같이 주어지므로
\[ D=R_{tr} \cos \lambda_{lat} \tag{13} \]
높이 \(h\) 를 포함한 경도 방향의 미소 거리 \(ds_{lon}\) 는 다음과 같이 계산된다.
\[ ds_{lon}=(R_{tr}+h) \cos \lambda_{lat} d \lambda_{lon} \tag{14} \]
\(D\) 를 계산하는 과정은 이전 포스트 글을 참조하기 바란다.
ECEF 좌표계와 LLH 좌표계
지구중심지구고정 좌표계(ECEF, earth-centered earth-fixed frame)는 지구의 중심에 원점이 위치하며 지구에 고정되어 있어서 지구와 함께 자전하는 좌표계이다. 지구와 함께 자전한다는 점에서 ECI 좌표
pasus.tistory.com
반면에 자오선은 타원 모양을 가지므로 특정 위도의 변화에 대한 지구 표면의 거리를 결정하려면 자오선 평면의 곡률 반경을 먼저 계산해야 한다. 곡률 반경은 다음과 같이 정의된다.
\[ \rho= \frac{ds}{d \phi } \tag{15} \]
여기서 \(s\) 는 호 길이이고 \(\phi\) 는 접선 각도다. 다소 복잡한 계산 과정을 거치면 특정 위도 \(\lambda_{lat}\) 에서 곡률 반경 방정식을 다음과 같이 계산할 수 있다.
\[ \rho_m = \frac{ R_{eq} (1-e_{er}^2) }{ (1-e_{er}^2 \sin^2 \lambda_{lat} )^{3/2} } \tag{16} \]
위 식은 식 (11)로 주어진 자오선 반경(meridian radius) \(R_{mr}\) 과 동일한 것으로 자오선 반경이 곧 타원의 곡률 반경이라는 것을 알 수 있다.
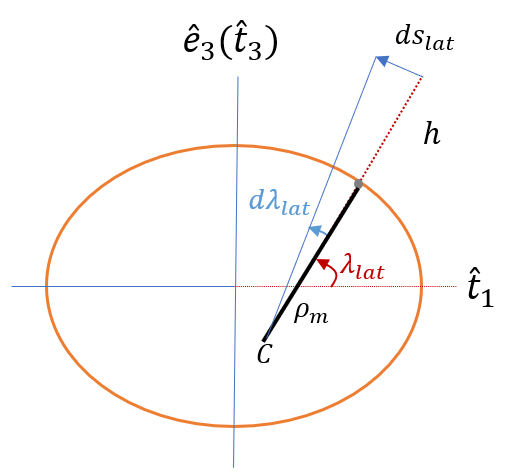
따라서 높이 \(h\) 를 포함한 위도의 미소 변화 \(d \lambda_{lat}\) 에 대한 위도 방향의 미소 거리 \(ds_{lat}\) 는 다음과 같이 계산된다.
\[ ds_{lat}=(R_{mr}+h)d \lambda_{lat} \tag{17} \]
NED 좌표계에서 위도 방향 속도는 북쪽(N) 방향 속도 \(v_N\) 이고 경도 방향 속도는 동쪽(E) 방향 속도 \(v_E\) 이다. 식 (14)와 식 (17)에 의하면 다음과 같은 식을 얻을 수 있다.
\[ \begin{align} & v_N = \frac{ds_{lat} }{dt} =(R_{mr}+h) \frac{d \lambda_{lat}}{dt} \tag{18} \\ \\ & \ \ \ \ \ = \dot{\lambda}_{lat} (R_mr+h) \\ \\ &v_E= \frac{ds_{lon}}{dt}=(R_{tr}+h) \cos \lambda_{lat} \frac{ d\lambda_{lon}}{dt} \\ \\ & \ \ \ \ \ = \dot{\lambda}_{lon} (R_{tr}+h) \cos \lambda_{lat} \end{align} \]
한편 NED 좌표계의 Down 방향은 높이 방향과 반대이므로,
\[ v_D= - \dot{h} \tag{19} \]
가 된다. 식 (18), (19)와 식 (10)을 비교해보면 서로 일치함을 알 수 있다.
'항공우주 > 비행역학' 카테고리의 다른 글
| 프로펠러기의 항속시간(Endurance)과 항속거리(Range) (0) | 2022.10.03 |
|---|---|
| 제트기의 항속시간(Endurance)과 항속거리(Range) (0) | 2022.10.02 |
| 원형 지구 가정에 의한 미사일 운동 방정식 유도 (0) | 2021.12.23 |
| 평평한 지구 가정에 의한 미사일 운동 방정식 유도 (0) | 2021.12.22 |
| ECEF 좌표계에서 미사일 운동 방정식 유도 (0) | 2021.12.21 |




댓글