지구중심지구고정 좌표계(ECEF, earth-centered earth-fixed frame)는 지구의 중심에 원점이 위치하며 지구에 고정되어 있어서 지구와 함께 자전하는 좌표계이다.
지구와 함께 자전한다는 점에서 ECI 좌표계와는 다르다. 기호로는 {e}로 표시한다.
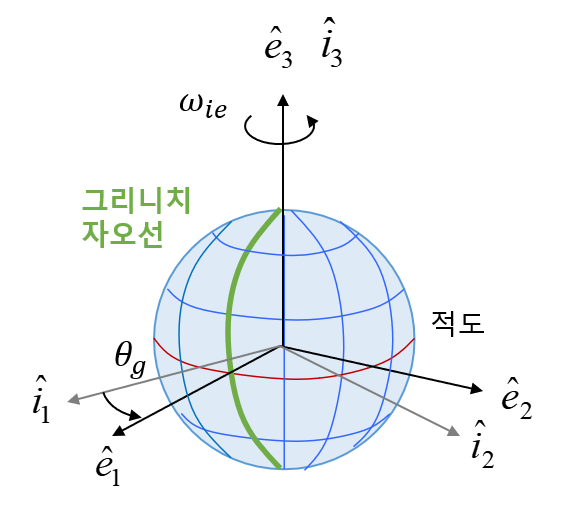
좌표계의 \(\hat{e}_1-\hat{e}_2\) 평면은 지구의 적도면에 위치한다. \(\hat{e}_3\) 축은 ECI 좌표계의 \(\hat{i}_3\) 와 같은 방향으로 지구의 자전축 방향이며 \(\hat{e}_1\) 축은 지구 적도와 본초 자오선(prime meridian)이 교차하는 점을 향하며, \(\hat{e}_2\) 축은 오른손 법칙에 의해 정해진다. 본초 자오선이란 경도의 기준이 되는 자오선으로, 경도 0도를 정의한다. 역사적으로는 영국 그리니치 천문대의 자오선이 국제 표준으로 채택되었으며, 오늘날에는 국제지구참조계(IERS Reference Meridian)가 본초 자오선으로 사용된다.
ECI 좌표계에 대한 ECEF 좌표계의 각속도 벡터는 \(^i \vec{\omega}^e =\omega_{ie} \hat{e}_3\) 이며 지구자전 각속도 \(\omega_{ie}\) 는 약 \(360^0/day\) 로서 WGS-84(World Geodetic System 1984)의 국제 표준값은 \(\omega_{ie}=7.291151467 \times 10^{-5} \ rad/sec\) 이다.
ECI좌표계에서 ECEF좌표계로의 DCM(방향코사인행렬)은 다음과 같다.
\[ C_e^i=C(z, \theta_g )= \begin{bmatrix} \cos \theta_g & -\sin \theta_g & 0 \\ \sin \theta_g & \cos \theta_g & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{1} \]
여기서 \(\theta_g\) 는 ECI 좌표계에서 ECEF 좌표계로의 회전각으로 그리니치 평균항성시(GMST, Greenwich Mean Sidereal Time) 또는 그리니치 각이라고 한다.
LLH(latitude-longitude-height) 좌표계는 물체의 위치를 위도, 경도, 높이로 표시하는 좌표계로서 지리 좌표계(geodetic frame)라고도 한다.
다음 그림에서 점 \(P\) 는 LLH 좌표계로 표현하고자 하는 관심 위치이며 점 \(P^\prime\) 은 중력가속도 방향으로 지구 자오선, 즉 타원상에 투사한 점이다. 지구는 자전의 영향으로 적도부분이 약간 부풀어 오른 타원체이다. 중력가속도 방향은 지구 중심을 향하지 않으며 타원의 접선과 직각방향이라는 데 주의해야 한다.

경도 (\(\lambda_{lon}\))는 본초 자오선 평면과 점 \(P^\prime\) 을 통과하는 자오선 평면과의 각도로 정의하며, 위도 (\(\lambda_{lat}\))는 점 \(P^\prime\) 에서 중력가속도 방향과 적도면과의 각도로 정의한다. 높이 (\(h\))는 점 \(P^\prime\) 과 \(P\) 의 거리로 정의하는데, 기하학적으로 정의된 지구 타원과 실제 지표와는 다르기 때문에 일반적인 지표상의 높이와는 다르다.
LLH 좌표계는 직교 좌표계가 아니기 때문에 DCM 관계식으로는 표현할 수 없다. ECEF 좌표계와 LLH 좌표계간의 상호 변환식을 유도해 보자.
다음 그림과 같이 점 \(P\) 를 관심 위치, 벡터 \(\vec{r}\) 을 점 \(P\) 까지의 위치벡터, 점 \(P^\prime\) 을 지표상의 투사점이라고 하자. ECEF 좌표계의 \(\hat{e}_3\) 축으로 경도 \(\lambda_{lon}\) 만큼 회전시켜 만든 임시 좌표계를 \(\{t\}\) 좌표계라고 한다.
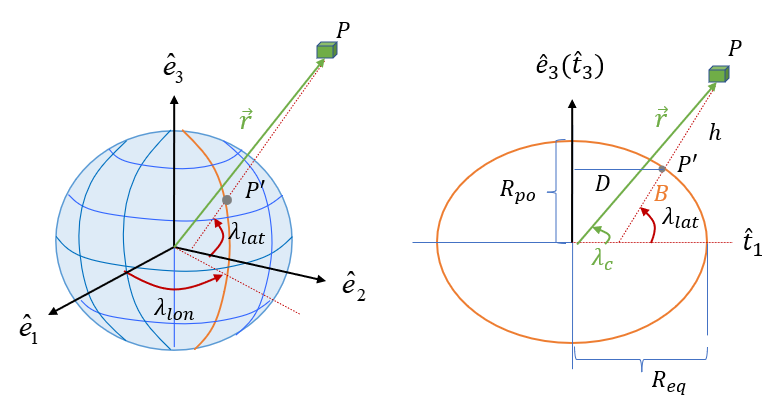
지구 중심에서 점 \(P^\prime\) 까지의 거리를 \(r_0\) 라고 하고, \(\hat{t}_1\) 축과의 각을 지구중심 위도 \(\lambda_c\) 라고 한다. 점 \(P^\prime\) 의 \(\hat{t}_1\) 축과 \(\hat{t}_3\) 축으로의 성분을 각각 구하면 다음과 같다.
\[ x=r_0 \cos \lambda_c, \ \ \ z=r_0 \sin \lambda_c \tag{2} \]
위 식으로부터 \(\lambda_c\) 를 구하면
\[ \tan \lambda_c = \frac{z}{x} \tag{3} \]
이다. 한편 점 \(P^\prime\) 은 지구 타원상의 한 점이므로 다음 식을 만족한다.
\[ \frac{x^2}{R_{eq}^2 }+ \frac{z^2}{R_{po}^2 }=1 \tag{4} \]
여기서 \(R_{eq}\) 는 지구 적도 반지름, \(R_{po}\) 는 극 반지름이다. 식 (2)를 (4)에 대입하면,
\[ r_0= \left( \frac{ \cos^2 \lambda_c }{ R_{eq}^2 } + \frac{ \sin^2 \lambda_c }{R_{po}^2 } \right)^{-1/2} \tag{5} \]
가 된다. 점 \(P^\prime\) 에서 접선을 구하기 위하여 식 (4)를 미분하면,
\[ \frac{ 2xdx}{R_{eq}^2} + \frac{2zdz}{R_{po}^2 }=0 \tag{6} \]
이 되고, 이 식과 식 (3)으로부터 접선의 방정식은
\[ \frac{dx}{dz} = - \frac{R_{eq}^2}{R_{po}^2} \ \frac{2z}{2z} =- \frac{R_{eq}^2}{R_{po}^2 } \tan \lambda_c \tag{7} \]
로 구할 수 있다. 한편, 점 \(P^\prime\) 에서 접선은 다음 식으로도 구할 수 있으므로,
\[ \frac{-dx}{dz} = \tan \lambda_{lat} \tag{8} \]
식 (8)과 (7)을 이용하면 지구중심 위도 (\(\lambda_c\))와 위도 (\(\lambda_{lat}\))의 관계식을 다음과 같이 구할 수 있다.
\[ \tan \lambda_{lat} = \frac{ R_{eq}^2 }{R_{po}^2} \tan \lambda_c \tag{9} \]
길이 \(D\) 를 점 \(P^\prime\) 의 \(\hat{t}_1\) 축 성분이라고 하면 식 (5와 (9)를 이용하여 길이 \(D\) 는 다음과 같이 계산된다.
\[ \begin{align} D &= r_0 \cos \lambda_c = \frac{ \cos \lambda_c }{ \sqrt{ \frac{\cos^2 \lambda_c }{R_{eq}^2 } + \frac{ \sin^2 \lambda_c }{R_{po}^2} } } \tag{10} \\ \\ &= \frac{ R_{eq}^2 \cos \lambda_{lat}} { \sqrt{ R_{eq}^2 \cos^2 \lambda_{lat} + R_{po}^2 \sin^2 \lambda_{lat} }} \end{align} \]
\(R_{po}^2=R_{eq}^2 (1-e_{er}^2)\) 의 관계식을 이용하면, 식 (10)은
\[ \begin{align} D &= \frac{ R_{eq} \cos \lambda_{lat} }{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat}}} \tag{11} \\ \\ &= R_{tr} \cos \lambda_{lat} \end{align} \]
가 된다. 여기서 \(R_{tr}\) 을 접선반경(tangential radius)이라고 하며 다음과 같이 정의한다.
\[ R_{tr} = \frac{ R_{eq} }{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat}}} \tag{12} \]
한편 길이 \(B\) 도 길이 \(D\) 와 비슷한 방법으로 계산할 수 있으며 다음과 같이 주어진다.
\[ \begin{align} B &= \frac{r_0 \sin \lambda_c }{ \sin \lambda_{lat}} \tag{13} \\ \\ &= R_{tr} (1-e_{er}^2) \end{align} \]
이제, 관심 위치 점 \(P\) 를 임시 좌표계 \(\{t\}\) 로 표현하면 다음과 같다.
\[ \vec{r}= (D+h \cos \lambda_{lat}) \ \hat{t}_1 + (B+h) \sin \lambda_{lat} \ \hat{t}_3 \tag{14} \]
식 (11)과 (13)을 식 (14)에 대입하고, ECEF 좌표계와 임시 좌표계 \(\{t\}\) 간의 DCM이 \(C_t^e=C(z, \lambda_{lon})\) 임을 감안하여 식 (14)의 벡터 \(\vec{r}\) 을 ECEF 좌표계로 표현하면 다음과 같다.
\[ r^e = \begin{bmatrix} (R_{tr}+h) \cos \lambda_{lat} \cos \lambda_{lon} \\ (R_{tr}+h) \cos \lambda_{lat} \sin \lambda_{lon} \\ \left( R_{tr} (1-e_{er}^2 )+h \right) \sin \lambda_{lat} \end{bmatrix} \tag{15} \]
위 식이 LLH 좌표계에서 ECEF 좌표계로 좌표 변환하는 식이다.
이와 반대로 ECEF 좌표계를 LLH 좌표계로 변환하는 문제는 간단치 않으며 반복계산법이 요구된다. 우선 관심 위치가 ECEF 좌표계에서 다음과 같이 주어졌다고 가정한다.
\[ r^e= \begin{bmatrix} r_1 & r_2 & r_3 \end{bmatrix}^T \tag{16} \]
식 (16)은 식 (15)와 같기 때문에 두 식으로부터 경도 \(\lambda_{lon}\) 를 구하면 다음과 같다.
\[ \frac{ r_2}{ r_1} = \frac{ \sin \lambda_{lon}} {\cos \lambda_{lon}} = \tan \lambda_{lon} \tag{17} \]
높이 \(h\) 를 구하기 위하여 식 (15)와 식 (16)의 \(r_1\) 과 \(r_2\) 를 이용하면
\[ \sqrt{r_1^2+r_2^2 }= (R_{tr}+h) \cos \lambda_{lat} \tag{18} \]
와 같다. 따라서 \(h\) 는 위도 \(\lambda_{lat}\) 이 주어지면 다음과 같이 계산할 수 있다.
\[ h= \frac{ \sqrt{r_1^2+r_2^2 }}{ \cos \lambda_{lat}} -R_{tr} \tag{19} \]
한편, 식 (15)에서 \(r_3\) 를 이용하면,
\[ \frac{r_3}{ \sqrt{r_1^2+r_2^2 }} = \frac{ \left( R_{tr} (1-e_{er}^2 )+h \right) \sin \lambda_{lat} }{(R_{tr}+h) \cos \lambda_{lat}} \tag{20} \]
가 되므로 높이 \(h\) 가 주어지면 \(\lambda_{lat}\) 은 다음과 같이 계산할 수 있다.
\[ \tan \lambda_{lat} = \frac{r_3}{ \sqrt{r_1^2+r_2^2 }} \left( 1- \frac{e_{er}^2 R_{tr}}{R_{tr}+h} \right)^{-1} \tag{21} \]
위 식은 겉보기에 명시적(explicit)인 식으로 보이지만 접선반경 \(R_{tr}\) 도 \(\lambda_{lat}\) 의 함수이기 때문에 암시적(implicit)인 식임에 주의해야 한다.
높이 \(h\) 와 위도 \(\lambda_{lat}\) 은 식 (19)와 (21)을 이용하여 반복계산법으로 구하면 된다. 즉,
\[ \mbox{guess } \lambda_{lat} \to R_{tr} \to h \to \lambda_{lat} \to R_{tr} \to h \to \cdots \]
'항공우주 > 우주역학' 카테고리의 다른 글
| 상대 궤도운동 방정식 (Relative Orbit Equation of Motion) (0) | 2023.01.20 |
|---|---|
| ECEF-LLH 좌표계 상호 변환 매트랩 코드 (1) | 2022.01.01 |
| SCI 좌표계와 ECI 좌표계 (0) | 2021.12.30 |
| 기본 궤도 미분 방정식의 무차원화 (0) | 2021.12.30 |
| 궤도 에너지와 속도 (0) | 2021.12.14 |




댓글