Navier-Stokes 방정식은 뉴톤 제2법칙으로부터 유도될 수 있다. 공기를 비롯한 유체는 고체와 달리 정해진 모양이 없기 때문에 뉴톤 제2법칙을 적용하기 위해서는 특별한 아이디어가 필요하다.
공기와 같은 속도로 움직이는 미소 유체요소(infinitesimal fluid element)를 생각해보자. 이 유체요소는 일정한 질량을 가지고 있으며, 질량을 유지하기 위해서 부피는 변할 수 있다고 가정한다. 이 유체요소를 질점으로 보면 뉴톤 제2법칙을 적용할 수 있다.
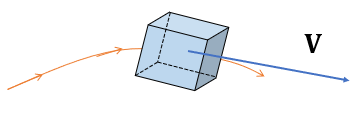
이 유체요소에 작용하는 힘은 체적력(body force), 압력, 그리고 점성력(viscous force)이 있다. 먼저 체적력에는 대표적으로 중력이 있으며 이밖에 관성력과 전자기력 등이 있다. 체적력 \(d\mathbf{F}_b\) 를 단위 질량당 체적력인 \(\mathbf{f}\) 를 이용해 표현하면 다음과 같다.
\[ d\mathbf{F}_b=dxdydz \ (\rho f_x \ \mathbf{i} + \rho f_y \ \mathbf{j} + \rho f_z \ \mathbf{k} ) \tag{1} \]
가 된다. 여기서 \(dx, dy, dz\) 는 유체요소의 각 변의 길이이며 \(\rho\) 는 밀도, \(f_x, f_y, f_z\) 는 단위질량장 체적력의 각 축 성분이다.
압력은 유체요소의 표면에 작용하는 표면력(surface force)으로서 표면에 수직으로 작용한다. 먼저 그림에 표시된 대로 \(x\) 축 방향의 압력을 계산해 보자.
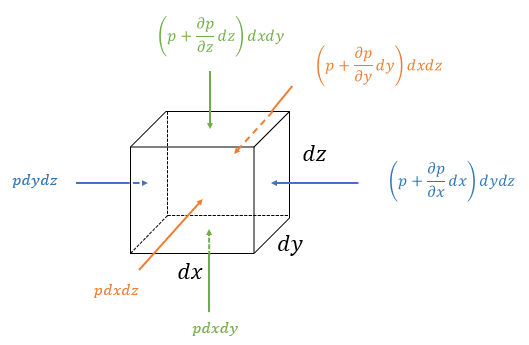
\[ \begin{align} dF_{px} &= p \ dydz - \left( p+ \frac{\partial p}{\partial x} dx \right) dydz \\ \\ &= - \frac{\partial p}{\partial x} dxdydz \end{align} \]
\(y, z\) 축 방향도 같은 방법으로 계산하면 유체요소에 작용하는 총 압력 \(d \mathbf{F}_p\) 는 다음과 같다.
\[ d \mathbf{F}_p= -dxdydz \left( \frac{\partial p}{\partial x} \ \mathbf{i} +\frac{\partial p}{\partial y} \ \mathbf{j} + \frac{\partial p}{\partial z} \ \mathbf{k} \right) \tag{2} \]
점성력도 유체요소의 표면에 작용하는 표면력으로서 표면에 수직으로 작용하는 수직응력(normal stress)과 평행하게 작용하는 전단응력(shear stress)로 나눠진다.
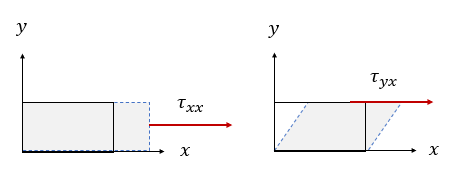
먼저 그림에 표시된 대로 \(x\) 축 방향의 점성력을 계산해 보자.
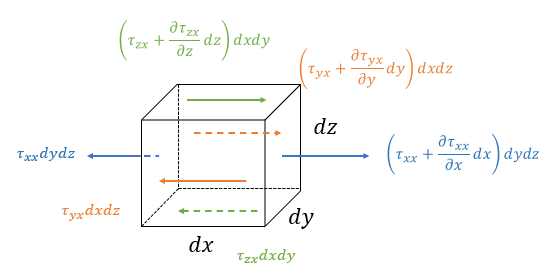
\[ \begin{align} dF_{vx} &= \left( \tau_{xx} + \frac{\partial \tau_{xx}}{\partial x} dx \right) dydz - \tau_{xx} dydz \\ \\ & \ \ \ + \left( \tau_{yx} + \frac{\partial \tau_{yx}}{\partial y} dy \right) dxdz - \tau_{yx} dxdz \\ \\ & \ \ \ + \left( \tau_{zx} + \frac{\partial \tau_{zx}}{\partial z} dz \right) dxdy - \tau_{zx} dxdy \\ \\ &= dxdydz \ \left( \frac{\partial \tau_{xx}}{\partial x} +\frac{\partial \tau_{yx}}{\partial y}+ \frac{\partial \tau_{zx}}{\partial z} \right) \end{align} \]
\(y, z\) 축 방향도 같은 방법으로 계산하면 유체요소에 작용하는 총 점성력 \(d\mathbf{F}_v\) 는 다음과 같다.
\[ \begin{align} d\mathbf{F}_v &= dxdydz \ \left( \frac{\partial \tau_{xx}}{\partial x} +\frac{\partial \tau_{yx}}{\partial y}+ \frac{\partial \tau_{zx}}{\partial z} \right) \ \mathbf{i} \tag{3} \\ \\ & \ \ \ + dxdydz \ \left( \frac{\partial \tau_{xy}}{\partial x} +\frac{\partial \tau_{yy}}{\partial y}+ \frac{\partial \tau_{zy}}{\partial z} \right) \ \mathbf{j} \\ \\ & \ \ \ + dxdydz \ \left( \frac{\partial \tau_{xz}}{\partial x} +\frac{\partial \tau_{yz}}{\partial y}+ \frac{\partial \tau_{zz}}{\partial z} \right) \ \mathbf{k} \end{align} \]
한편 유체요소의 가속도를 속도를 미분해서 계산할 수 있다. 먼저 \(x\) 축 방향의 속도 \(u(x, y, z, t)\) 를 미분해 보자.
\[ \begin{align} \frac{du}{dt} &= \frac{\partial u}{\partial x} \frac{dx}{dt} + \frac{\partial u}{\partial y} \frac{dy}{dt}+ \frac{\partial u}{\partial z} \frac{dz}{dt} + \frac{\partial u}{\partial t} \\ \\ &= u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}+ w \frac{\partial u}{\partial z} + \frac{\partial u}{\partial t} \end{align} \]
\(y, z\) 축 방향도 같은 방법으로 계산하면 유체요소의 가속도는 다음과 같이 계산된다.
\[ \begin{align} \frac{d \mathbf{V}}{dt} &= \left( u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}+ w \frac{\partial u} {\partial z} + \frac{\partial u}{\partial t} \right) \ \mathbf{i} \tag{4} \\ \\ & \ \ + \left( u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}+ w \frac{\partial v} {\partial z} + \frac{\partial v}{\partial t} \right) \ \mathbf{j} \\ \\ & \ \ + \left( u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y}+ w \frac{\partial w} {\partial z} + \frac{\partial w}{\partial t} \right) \ \mathbf{k} \end{align} \]
위 식은 속도벡터 \(\mathbf{V}\) 와 연산자 \(\nabla\) 를 사용하면 다음과 같이 고쳐 쓸 수 있다.
\[ \begin{align} \frac{d\mathbf{V}}{dt} &= \left( \frac{\partial u}{\partial t} + \mathbf{V} \cdot \nabla u \right) \mathbf{i} +\left( \frac{\partial v}{\partial t} + \mathbf{V} \cdot \nabla v \right) \mathbf{j} + \left( \frac{\partial w}{\partial t} + \mathbf{V} \cdot \nabla w \right) \mathbf{k} \tag{5} \\ \\ &= \frac{\partial \mathbf{V}}{\partial t}+ ( \mathbf{V} \cdot \nabla ) \mathbf{V} \end{align} \]
유체요소의 질량 \(dm=\rho \ dxdydz\) 는 일정하다고 가정했으므로 뉴톤의 제2법칙에 의하면
\[ \rho \ dxdydz \frac{d\mathbf{V}}{dt} = d \mathbf{F}_b + d \mathbf{F}_p + d \mathbf{F}_v \tag{6} \]
이 성립한다. 식 (1), (2), (3), (5)를 식 (6)에 대입하고 \(x, y, z\) 축 성분으로 나누어서 식을 쓰면 다음과 같이 된다.
\[ \begin{align} & \rho \left( \frac{\partial u}{\partial t} + \mathbf{V} \cdot \nabla u \right) = -\frac{\partial p}{\partial x} + \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + \rho f_x \tag{7} \\ \\ & \rho \left( \frac{\partial v}{\partial t} + \mathbf{V} \cdot \nabla v \right) = -\frac{\partial p}{\partial y} + \frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \tau_{yy}}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} + \rho f_y \\ \\ & \rho \left( \frac{\partial w}{\partial t} + \mathbf{V} \cdot \nabla w \right) = -\frac{\partial p}{\partial z} + \frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{yz}}{\partial y} + \frac{\partial \tau_{zz}}{\partial z} + \rho f_z \end{align} \]
위 식에 의하면 미지수가 \(u, v, w, p, \rho, \tau_{xx}, ...\) 등 14개에 달한다. 반면 식은 식 (7)로 주어지는 3개와 연속 방정식 1개 등 4개 밖에 안된다. 따라서 더 많은 식을 찾아내야 한다.
유체의 점성은 유체의 변형에 대항하는 저항력과 같은 역할을 하는데 전단응력이 유체의 점성과 관련이 있다. 아래 그림과 같이 물체의 표면 주위를 흐르는 유체는 점성 때문에 표면에서는 속도가 \(0\) 이고 표면으로부터의 거리에 따라 유속이 달라진다.
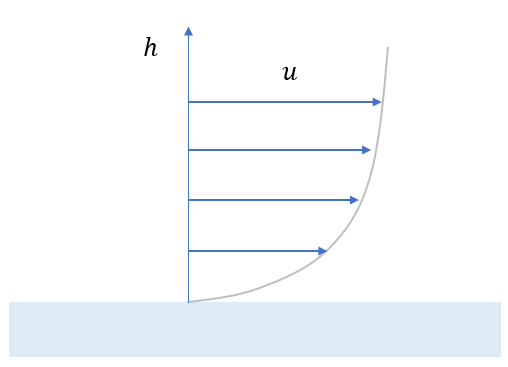
속도가 느린 유동층은 속도가 빠른 유동층에 힘을 가하여 속도가 느려지게 하고, 반대로 속도가 빠른 층은 속도가 느린 층에 반대의 힘을 가하여 속도가 느려지게 하는데 이와 같은 속도의 차이 때문에 전단응력이 발생하게 된다.
뉴톤유체(Newtonian fluid)는 전단응력 \(\tau\) 와 속도 변화율 사이에 비례관계가 성립하는 유체로서 다음과 같은 관계식을 갖는다.
\[ \tau = \mu \frac{du}{dh} \tag{8} \]
여기서 비례상수 \(\mu\) 를 점성계수(viscosity coefficient)라고 한다.
식 (7)의 유체가 뉴톤유체라는 가정을 하면 다음 식이 추가로 얻어진다.
\[ \begin{align} & \tau_{xy}= \tau_{yx} =\mu \left( \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \right) \tag{9} \\ \\ & \tau_{xz}= \tau_{zx} =\mu \left( \frac{\partial w}{\partial x} + \frac{\partial u}{\partial z} \right) \\ \\ & \tau_{yz}= \tau_{zy} =\mu \left( \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} \right) \end{align} \]
한편, 수직응력은 점성력뿐만 아니라 유체요소가 일정한 질량을 유지하기 위한 팽창과 수축 과정에서의 저항력도 고려해야 하므로 다음과 같은 관계식을 갖는다.
\[ \begin{align} & \tau_{xx} = \lambda ( \nabla \cdot \mathbf{V} ) + 2 \mu \frac{\partial u}{\partial x} \tag{10} \\ \\ & \tau_{yy} = \lambda ( \nabla \cdot \mathbf{V} ) + 2 \mu \frac{\partial v}{\partial y} \\ \\ & \tau_{zz} = \lambda ( \nabla \cdot \mathbf{V} ) + 2 \mu \frac{\partial w}{\partial z} \\ \\ \end{align} \]
여기서 \(\lambda\) 를 제2의 점성계수라고 하는데 Stokes는 이 값을 \(\lambda= -\frac{2}{3} \mu\) 일 것으로 생각하였다. Stokes의 가설이 맞는지 여부는 아직 명확히 확인되지 않았다고 한다. 식 (7), (9), (10)을 Navier-Stokes 방정식이라고 한다.
'항공우주 > 항공역학' 카테고리의 다른 글
| Vorticity의 정의 (0) | 2022.05.29 |
|---|---|
| 유동장의 시간미분에 대해서 (0) | 2022.05.24 |
| Navier-Stokes 방정식의 벡터 표현 (0) | 2021.10.22 |
| Navier-Stokes 방정식 - 2 (0) | 2021.08.10 |
| 연속 방정식 (continuity equation) (0) | 2021.08.09 |




댓글