홀로노믹 구속 (Holonomic Constraint)과 가상 변위

어떤 시스템을 구성하고 있는 질점들이 자유롭게 움직이지 못하고 운동학적으로 제약을 받고 있다면 그 시스템은 구속(constraint)되어 있다고 한다. 그리고 운동학적인 제약사항을 위치, 속도, 시간 등의 함수로 표현한 것을 구속조건 식이라고 한다.

 

 

예를 들면 3차원 공간 상에 두 질점이 길이가 $L$ 인 막대기로 연결되어 있을 경우, 두 질점은 자유롭게 운동하지 못하고 다음 구속조건 식을 만족하면서 운동해야 한다.

 

$$\begin{array}{}\text{(1)}& (x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2=L^2\end{array}$$

 

 

 

구속조건은 구속조건식의 형태에 따라 크게 홀로노믹 구속(holonomic constraint)과 비홀로노믹 구속(nonholonomic constraint)으로 분류된다.

홀로노믹 구속은 구속 조건식을 위치와 시간만의 함수로 표현할 수 있는 경우를 말한다. 예를 들면 위에서 언급한 길이가 $L$ 인 막대기로 연결되어 있는 두 질점의 운동과 같은 경우이다. 홀로노믹 구속 조건식의 일반적인 형태는 다음과 같다.

 

$$\begin{array}{}\text{(2)}& {\varphi }_j(x_1,y_1,z_1,...,x_N,y_N,z_N,t)=0,j=1,...,m\end{array}$$

 

여기서 $N$ 은 시스템을 구성하는 질점의 수이며, $(x_i,y_i,z_i)$ 는 질점 $i$ 의 좌표, 그리고 $m$ 은 구속조건의 갯수이다.

설명을 간단하게 하기 위해서 질점이 1개인 경우를 살펴본다. 먼저 질점이 어떤 곡면 상에서만 운동할 수 있다고 하자. 그 곡면의 식은 다음과 같이 주어진다.

 

$$\begin{array}{}\text{(3)}& \varphi (x,y,z)=0\end{array}$$

 

질점은 곡면 식을 만족해야 하므로 운동이 자유롭지 못하고 구속되어 있다. 또한 구속조건 식이 식 (2)의 형태이므로 홀로노믹 구속이다. 질점이 실제로 움직일 수 있는 극소 변위 $d\mathbf{r}$ 은 위 식을 미분하면 얻을 수 있다.

 

$$\begin{array}{}\text{(4)}& \frac{\partial \varphi }{\partial x}dx+\frac{\partial \varphi }{\partial y}dy+\frac{\partial \varphi }{\partial z}dz=0\end{array}$$

 

여기서 변위 $d\mathbf{r}$ 또는 $(dx,dy,dz)$ 는 곡면의 접선에 해당하고 질점이 움직일 수 있는 가능한 변위를 뜻한다. 이 중 하나가 질점이 실제로 움직인 변위가 될 것이다.

한편 질점의 운동을 곡면 상으로 제약하려면 그것을 가능하게 하는 힘이 필요하다. 이 힘을 구속력(constraint force)이라고 한다. 구속력은 곡면이 질점에 가하는 힘이다. 곡면이 마찰이 없는 매끄러운 표면을 가졌다면 구속력은 곡면에 수직인 방향으로 작용한다. 만약 마찰이 있다면 곡면 상에서 질점이 움직이는 방향의 반대 방향으로 마찰력이 작용하지만 이러한 마찰력은 구속력과는 다르게 취급할 수 있다.

구속력을 ${\mathbf{F}}^{\prime }$ 로 표기하면 구속력은 곡면의 접선과 직각이므로 다음 식을 만족해야 한다.

 

$$\begin{array}{}\text{(5)}& {\mathbf{F}}^{\prime }\cdot d\mathbf{r}=0\end{array}$$

 

위 식은 구속력 ${\mathbf{F}}^{\prime }$ 가 질점에 한 일($dW$)이기도 하므로, '구속력이 질점의 실제 가능한 변위를 따라가면서 한 일은 0 이다'라고 말할 수 있다.

구속력은 접선과 직각이므로 다음과 같이 곡면의 그래디언트와 평행한 것으로 표현할 수 있다.

 

$$\begin{array}{}\text{(6)}& {\mathbf{F}}^{\prime }=\lambda \mathrm{\nabla }\varphi \end{array}$$

또는

 

$$\begin{array}{}\text{(7)}& \frac{F_x^{\prime }}{\frac{\partial \varphi }{\partial x}}=\frac{F_y^{\prime }}{\frac{\partial \varphi }{\partial y}}=\frac{F_z^{\prime }}{\frac{\partial \varphi }{\partial z}}=\lambda \end{array}$$

 

여기서 $\lambda$ 는 비례상수이다.

 

 

만약 곡면 식 자체가 시간의 함수라면 이야기가 조금 달라진다.

 

$$\begin{array}{}\text{(8)}& \varphi (x,y,z,t)=0\end{array}$$

 

위와 마찬가지로 질점이 실제로 움직일 수 있는 극소 변위 $d\mathbf{r}$ 은 위 식을 미분하면 얻을 수 있다.

 

$$\begin{array}{}\text{(9)}& \frac{\partial \varphi }{\partial x}dx+\frac{\partial \varphi }{\partial y}dy+\frac{\partial \varphi }{\partial z}dz+\frac{\partial \varphi }{\partial t}dt=0\end{array}$$

 

위 식에 의하면 극소 변위 $d\mathbf{r}$ 은 식 (4)의 $d\mathbf{r}$ 과는 다르다는 것을 알 수 있다.

 

 

하지만 구속력 ${\mathbf{F}}^{\prime }$ 은 여전히 곡면의 접선과 직각이어야 하므로 구속력이 실제 가능한 변위를 따라가면서 한 일은 구속력과 $d\mathbf{r}$ 이 직각이 아니므로 $0$ 이 아니다.

 

$$\begin{array}{}\text{(10)}& dW={\mathbf{F}}^{\prime }\cdot d\mathbf{r}\ne 0\end{array}$$

 

 

 

이제 새로운 변위를 도입한다. 바로 가상 변위(virtual displacement)다. 가상 변위는 시스템의 구속조건에는 부합하지만 가상적인 임의의 극소 변위를 말한다. 실제 극소 변위, 즉 미분은 $d$ 로 표기하는 반면, 가상 변위는 변분이라고 하며 $\delta$ 로 표기한다. 실제 변위는 시간 미분 $dt$ 동안 실제로 발생할 수 있는 변위이며 가상 변위는 시간 변화 없이 ($dt=0$) 가상적으로 만든 순간적인 변위이다.

실제 변위와 가상 변위는 일반적으로 다르다. 하지만 구속조건 식 자체가 시간의 함수가 아닐 때 두 변위는 동일한 구속조건 식을 만족하므로 같다. 즉, 시간의 함수가 아닌 홀로노믹 구속조건 식 $\varphi (x,y,z)=0$ 에서 가상 변위 $\delta \mathbf{r}$ 은 실제 변위 $d\mathbf{r}$ 과 마찬가지로 다음 식을 만족한다.

 

$$\begin{array}{}\text{(11)}& \frac{\partial \varphi }{\partial x}\delta x+\frac{\partial \varphi }{\partial y}\delta y+\frac{\partial \varphi }{\partial z}\delta z=0\end{array}$$

 

또한 구속조건 식이 시간의 함수인 $\varphi (x,y,z,t)=0$ 의 경우에도 가상 변위 $\delta \mathbf{r}$ 은 $dt=0$ 에서의 변위이므로 식 (11)을 만족한다. 즉 가상 변위는 홀로노믹 구속조건 식이 시간의 함수이건 아니건 구속력과 항상 직각이다. 따라서 구속력이 가상 변위를 따라가면서 한 가상일(virtual work)은 $0$ 이 된다. 즉,

 

$$\begin{array}{}\text{(12)}& \delta W={\mathbf{F}}^{\prime }\cdot \delta \mathbf{r}=0\end{array}$$

 

 

 

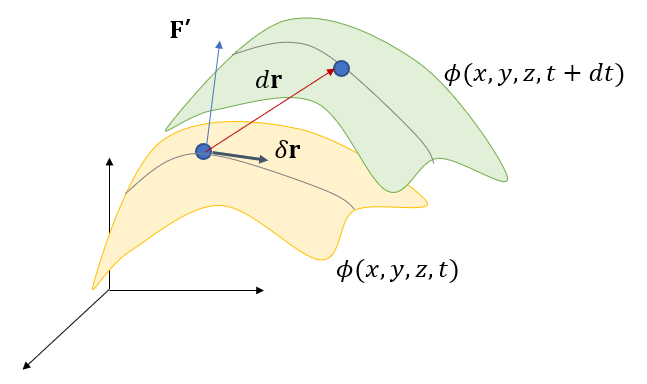
식 (9)는 홀로노믹 구속조건 식 $\varphi (x,y,z,t)=0$ 의 전미분(total differential)이다. 이 식을 일반화시키면 다음과 같이 표현할 수 있다.

 

$$\begin{array}{}\text{(13)}& a_{x}dx+a_{y}dy+a_{z}dz+a_{0}dt=0\end{array}$$

 

여기서 계수 $a_x,a_y,a_z,a_0$ 는 각각 $(x,y,z,t)$ 의 함수다. 식 (13)을 적분하여 $\varphi (x,y,z,t)=0$ 의 형태로 표현할 수 있다면 식 (13)도 홀로노믹 구속이 되지만, 만약 적분 가능하지 않다면 식 (13)을 비홀로노믹 구속조건 식이라고 한다.

비홀로노믹 조건식 (13)에서 변위 $d\mathbf{r}=(dx,dy,dz)$ 는 실제 가능한 변위를 나타내는 반면, 식 (14)는 가상 변위 $\delta \mathbf{r}$ 을 나타낸다.

 

$$\begin{array}{}\text{(14)}& a_x\delta x+a_y\delta y+a_z\delta z=0\end{array}$$

 

구속력은 구속의 결과로 생기는 힘이다. 외부에서 주어지는 힘과 구속력은 식 (13)을 만족하는 실제 운동을 결정한다. 하지만 구속력은 식 (14)의 가상 변위에 대해서 하는 일은 $0$ 이다. 이 때 구속력 ${\mathbf{F}}^{\prime }$ 는 계수 $(a_x,a_y,a_z)$ 와 비례하며 그 관계는 식 (7)과 유사하다.

 

$$\begin{array}{}\text{(15)}& \frac{F_x^{\prime }}{a_x}=\frac{F_y^{\prime }}{a_y}=\frac{F_z^{\prime }}{a_z}=\lambda \end{array}$$

 

외력은 알고 있거나 주어지는 경우가 많은 반면 구속력은 주어지지 않거나 계산하기 어렵다는 점에서 실제 일보다 가상일을 이용하는 데 장점이 있다.

한편, 비홀로노믹 구속조건 식은 식 (13)과 같이 주어지거나 혹은 다음과 같이 속도의 선형 식 형태로 표현하기도 한다.

 

$$\begin{array}{}\text{(16)}& a_x\dot{x}+a_y\dot{y}+a_z\dot{z}+a_0=0\end{array}$$

 

보다 일반적인 형태의 비홀로노믹 구속은 다음과 같이 위치, 시간뿐 만 아니라 속도까지 포함된 함수식으로 표현한다.

 

$$\begin{array}{}\text{(17)}& \psi (x,y,z,\dot{x},\dot{y},\dot{z},t)=0\end{array}$$

 

비홀로노믹 구속은 홀로노믹 구속이 아닌 모든 경우를 말한다. 구속 조건 관계식이 등식으로 주어지지 않고 부등식으로 주어지는 경우도 비홀로노믹 구속의 예다.

 

$$\begin{array}{}\text{(18)}& \varphi (x,y,z,t)\ge 0\end{array}$$