\(N\) 개의 질점으로 이루어진 시스템이 있다고 하자. 각 질점의 위치는 \(N\) 개의 위치 벡터 \(\mathbf{r}_k=\mathbf{r}_k (x_k, y_k, z_k ), \ \ k=1,...,N\) 으로 표현할 수 있다. 여기서 \(x_k, y_k, z_k\) 는 \(k\) 번째 질점의 위치를 직교 좌표계(Cartesian coordinate)로 표시한 좌표다. 질점이 운동할 경우 질점의 각 위치를 시간의 함수 \(x_k (t), y_k (t), z_k (t)\) 로 표현하면 된다. 그러면 3차원 공간상에 \(N\) 개의 운동 궤적이 나타날 것이다.
그런데 만약 \(3N\) 차원 공간이 있다면 \(N\) 개의 질점으로 이루어진 시스템의 운동을 한 점의 운동으로 표현할 수 있지 않을까. 이와 같이 시스템의 위치를 한 점으로 표현할 수 있는 공간을 형상공간(configuration space)라고 한다.
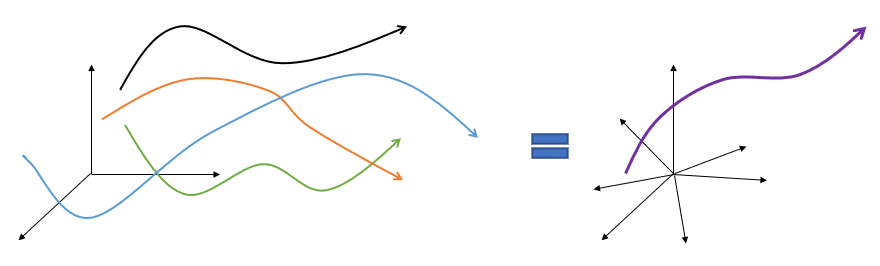
형상공간의 좌표를 일반화 좌표(generalized coordinate)라고 하고 보통 \(q_1, q_2, ... , q_n\) 으로 표시한다. 여기서 \(n=3N\) 이 된다. 그러면 일반화 좌표와 직교 좌표계에서 \(N\) 개의 질점의 좌표는 다음과 같은 좌표 변환 관계가 성립한다.
\[ \begin{align} & x_1=x_1 (q_1, q_2, ... , q_n ) \\ \\ & y_1=y_1 (q_1, q_2, ... , q_n ) \\ \\ & \ \ \ \ \ ... \\ \\ & z_N=z_N (q_1, q_2, ... ,q_n) \end{align} \]
여기서 일반화 좌표 \(q_i\) 는 단위가 모두 같을 필요는 없다. 각각의 좌표가 직교 좌표계와 같이 거리 단위도 될 수 있고, 각도이 될 수 있고 물리적 의미가 없는 어떤 양이 될 수도 있다. 심지어 푸리에 시리즈(Fourier series)의 계수가 될 수도 있다. 또한 같은 시스템에 대해서 여러 개의 서로 다른 일반화 좌표 세트가 있을 수도 있다.
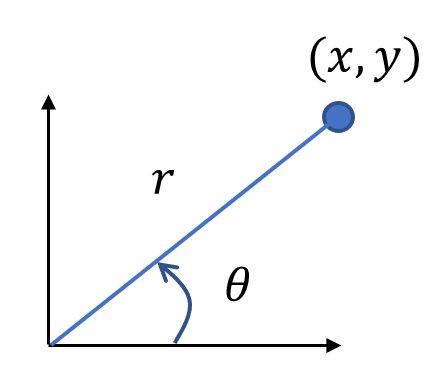
일반화 좌표는 시스템의 운동을 쉽게 기술할 수 있는 파라미터로 선정하면 된다. 예로서 평면에서 운동하는 어떤 질점이 있다고 할 때 질점의 위치를 다음과 같이 극좌표계 표현할 수 있다.
\[ \begin{align} & x=r \cos \theta \\ \\ &y= r \sin \theta \end{align} \]
그러면 여기서 \(r=q_1\) 과 \(\theta =q_2\) 가 일반화 좌표가 되는 것이다.
일반화 좌표를 이용하여 홀로노믹(holonomic) 구속조건 식을 표현하면 다음과 같다.
\[ \phi_j (q_1, q_2, ..., q_n, t)=0, \ \ \ j=1, ... , m \]
비홀로노믹(nonholonomic) 구속조건 식은 다음과 같이 표현된다.
\[ \sum_{i=1}^n a_{ji} (\mathbf{q},t ) d q_i +a_{j0} (\mathbf{q},t) dt=0, \ \ \ j=1, ... , m \]
여기서 \(\mathbf{q}=[q_1 \ q_2 \ ... \ q_n ]^T\) 이다.
일반화 좌표는 시스템이 구속조건을 가질 때 그 장점이 명확해진다. 예를 들면 2차원 평면 상에 두 질점이 길이가 \(L\) 인 막대기로 연결되어 있을 경우, 두 질점은 자유롭게 운동하지 못하고 다음 구속조건 식을 만족하면서 운동해야 한다.
\[ (x_1-x_2 )^2+(y_1-y_2 )^2=L^2 \]

두 질점이 평면상을 자유롭게 운동할 때에는 \(x_1, y_1, x_2, y_2\) 등 4개의 좌표가 필요하지만 구속조건 때문에 3개의 좌표만 있으면 두 질점의 운동을 기술할 수 있다. 왜냐하면 구속조건 식으로 한 개의 좌표를 다른 3개 좌표의 함수로 표현할 수 있기 때문이다. 이 때 만약 그림에 있는 것처럼 일반화 좌표를 \(x_1, y_1, \theta\) 로 선정한다면 두 질점의 운동을 좀 더 편리하게 기술할 수 있을 것이다.
원칙적으로 \(N\) 개의 질점으로 이루어진 시스템이 \(m\) 개의 구속조건을 가지고 있을 때 시스템의 운동은 \(n=3N-m\) 개의 독립적인 좌표 \(q_1, q_2, ... , q_n\) 만 있으면 표현이 가능하다. 여기서 \(n\) 을 시스템의 자유도(DOF, degree of freedom)이라고 한다. 시스템의 자유도는 시스템의 운동을 유일하게 기술하는데 필요한 최소의 독립적인 파라미터 개수를 말한다.
자유도가 \(n\) 인 경우 \(n\) 개의 일반화 좌표로 시스템의 운동을 기술할 수 있으면 좋겠지만 상황에 따라서는(비홀로노믹 구속의 경우) \(n\) 개 이상의 좌표가 필요한 경우도 많다. 그럴 때는 자유도를 초과하는 수만큼 구속조건 식의 개수를 유지해야 한다.
구속조건을 이용하여 일반화 좌표의 개수를 \(n \lt 3N\) 으로 만들 경우 일반화 좌표와 직교 좌표계간의 좌표 변환 관계식에 명시적으로 시간을 추가하는 것이 일반적인 형식이다. 왜냐하면 구속조건이 시간의 함수일 수 있기 때문이다.
\[ \begin{align} & x_1=x_1 (q_1, q_2, ... , q_n, t ) \\ \\ & y_1=y_1 (q_1, q_2, ... , q_n, t ) \\ \\ & \ \ \ \ \ ... \\ \\ & z_N=z_N (q_1, q_2, ... ,q_n, t) \end{align} \]
그러면 3차원 공간상의 실제 변위와 일반화 좌표의 실제 변위 사이의 관계식은 다음과 같다.
\[ d \mathbf{r}_k=\sum_{i=1}^n \frac{\partial \mathbf{r}_k}{\partial q_i } d q_i + \frac{\partial \mathbf{r}_k}{\partial t} dt \]
반면에 3차원 공간상의 가상 변위와 일반화 좌표의 가상 변위 사이의 관계식은 다음과 같다.
\[ \delta \mathbf{r}_k=\sum_{i=1}^n \frac{\partial \mathbf{r}_k}{\partial q_i } \delta q_i \]
'항공우주 > 동역학' 카테고리의 다른 글
| 해밀톤 방정식 (Hamilton’s Equation) (0) | 2021.08.08 |
|---|---|
| 라그랑지 방정식 (Lagrange’s Equation) (0) | 2021.08.08 |
| 해밀톤의 원리 (Hamilton’s Principle) (0) | 2021.08.04 |
| 홀로노믹 구속 (Holonomic Constraint)과 가상 변위 (0) | 2021.08.04 |
| 포텐셜 에너지 (Potential Energy) (0) | 2021.08.03 |




댓글