물체의 위치와 운동을 표현하기 위해서는 기준점과 기준 좌표계(reference frame)가 필요하다.
기준점을 좌표계의 원점이라고 하며 물체의 위치를 기준점으로부터 좌표계의 각 축 방향으로 얼마큼 떨어져 있는지 숫자로 나타낸다.

좌표계로는 좌표계의 각 축이 직각을 이루는 직교 좌표계(Cartesian coordinate system)가 주로 사용되지만, 원통 좌표계(cylindrical coordinate system)와 구 좌표계(spherical coordinate system)등도 많이 사용된다.
직교 좌표계에서는 3차원 공간의 경우 통상적으로 각 축을 \(x, y, z\)축이라고 하든가 아니면 \(\hat{i}, \hat{j}, \hat{k}\) 축이라고 표기한다. 하지만, 좌표계가 여러 개가 쓰일 경우에는 이와 같은 좌표 축의 표기 방법은 적절치가 않다.
보통 항공기나 로봇, 우주비행체 등 운동체의 운동을 수학식으로 표현하기 위해서는 여러 개의 좌표계가 필요하므로, 여기서는 좌표계와 해당 좌표계의 \(x, y, z\)축을 명확하게 표현하기 위하여 다음과 같은 표기법을 사용하기로 한다.
직교 좌표계는 중괄호로 된 영문 소문자로 표기한다. 즉 \(\{a\}\)는 좌표계의 이름이 \(a\) 라는 뜻이다. 좌표계 \(\{a\}\)의 \(x, y, z\)축은 각각 \(\hat{a}_1, \hat{a}_2, \hat{a}_3\) 으로 표시한다. 그러면 좌표계 \(\{b\}\)의 \(x, y, z\)축은 각각 \(\hat{b}_1, \hat{b}_2, \hat{b}_3\) 으로 표시하면 된다.
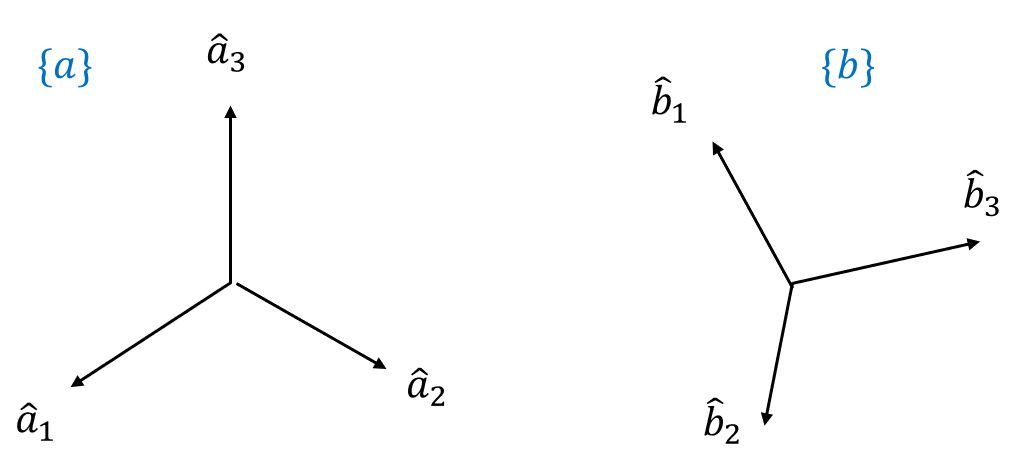
여기서 hat 기호는 단위벡터를 나타낸다. 단위벡터는 크기가 1인 벡터를 의미한다. 벡터는 크기와 방향으로 이루어져 있는데, 단위벡터는 크기가 1로 고정되어 있으므로 주로 방향을 지시하는 벡터로 사용된다.
이런 표기법에 의하면 직교 좌표계는 3개의 단위벡터가 기준점을 중심으로 서로 직각인 방향을 가리키는 세개의 축으로 구성되어 있다. 서로 직각인 경우가 2세트가 나오므로 보통 항공우주 분야에서는 오른손 법칙(right-hand rule)에 의한 3개의 직교 단위벡터로 정의되는 좌표계를 사용한다. 참고로 유니티 게임엔진에서는 왼손 법칙에 의한 직교 좌표계를 사용한다.
오른손 법칙이란 엄지를 제외한 오른손 4개 손가락을 \(x\)축에서 \(y\)축 방향으로 감아 쥘 때, 엄지 방향을 \(z\)축으로 삼는 법칙이다.
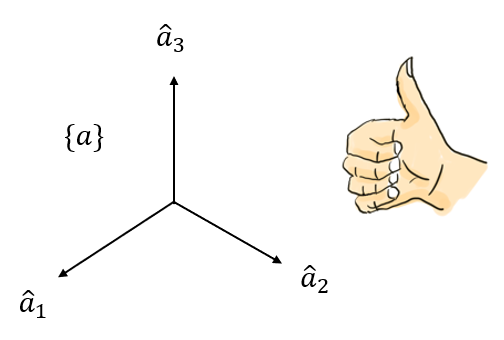
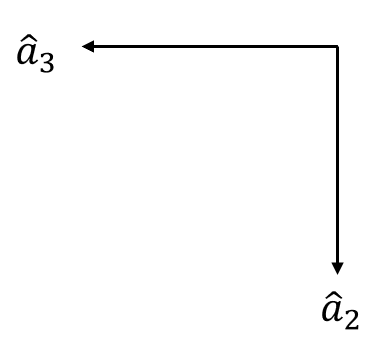
오른손 법칙에 의하면 다음 그림에서 \(z\)축은 화면 밖으로 나오는 방향이다.

다음 그림에서 \(x\)축은 화면 속으로 들어가는 방향이다.

'항공우주 > 동역학' 카테고리의 다른 글
| 오일러각 (Euler Angles) (0) | 2021.02.07 |
|---|---|
| 방향코사인행렬 (DCM) (1) | 2021.02.06 |
| 벡터를 직교 좌표계로 표현하기 (0) | 2021.02.05 |
| 자이로스코프 효과 (1) | 2021.01.10 |
| 경로 좌표계와 극 좌표계 (0) | 2021.01.09 |




댓글