벡터를 직교 좌표계로 표현하기

스칼라(scalar)는 크기만 가진 어떤 양이다. 반면에 벡터(vector)는 크기와 방향을 갖는 양이다.

 

 

벡터는 통상적으로 영문 소문자위에 화살표로 표기한다. 즉 벡터 $u$는 $\overrightarrow{u}$로 표기한다. 또한 벡터는 화살표로 그린다. 화살표의 크기는 벡터의 크기를 나타내며, 화살표의 방향은 벡터의 방향을 나타낸다.

 

 

벡터의 크기는 벡터의 절대값으로 표기한다. 벡터 $\overrightarrow{u}$의 크기는 $\left|\overrightarrow{u}\right|$다.

두 개의 벡터는 크기와 방향이 모두 같으면 '같다'고 한다. 아래 그림에서 두 벡터 $\overrightarrow{u}$와 $\overrightarrow{w}$는 출발점이 다르지만 크기와 방향이 같으므로 같다. 즉, $\overrightarrow{u}=\overrightarrow{w}$ 이다.

 

 

벡터는 특정 좌표계의 좌표축 성분으로 나누어 표현할 수 있다. 예를 들어 벡터 $\overrightarrow{u}$를 좌표계 $\{a\}$의 축 성분으로 표현하기 위해서는 다음과 같이 벡터 $\overrightarrow{u}$를 $\{a\}$의 좌표축을 나타내는 단위벡터가 가리키는 방향의 성분으로 나타내면 된다.

 

$$\begin{array}{rl}\overrightarrow{u}& =(\overrightarrow{u}\cdot {\hat{a}}_1){\hat{a}}_1+(\overrightarrow{u}\cdot {\hat{a}}_2){\hat{a}}_2+(\overrightarrow{u}\cdot {\hat{a}}_3){\hat{a}}_3\\ \\ & =u_1{\hat{a}}_1+u_2{\hat{a}}_2+u_3{\hat{a}}_3\end{array}$$

 

여기서 $u_1$은 벡터 $\overrightarrow{u}$의 $x$축 또는 단위백터 ${\hat{a}}_1$가리키는 방향의 성분이다. 왜냐하면

 

$$u_1=\overrightarrow{u}\cdot {\hat{a}}_1=\left|\overrightarrow{u}\right|\cos \theta$$

 

이기 때문이다. 여기서 $\theta$는 벡터 $\overrightarrow{u}$와 ${\hat{a}}_1$의 사잇각이므로 $u_1$은 벡터 $\overrightarrow{u}$를 단위벡터 ${\hat{a}}_1$이 가리키는 방향으로 투사한 길이가 된다.

 

 

마찬가지로 $u_2,u_3$도 각각 벡터 $\overrightarrow{u}$를 $y$축과 $z$축으로 투사한 길이가 된다. 즉, 각 축의 성분이 된다.

스칼라 $u_1$과 단위벡터 ${\hat{a}}_1$의 곱은 길이가 $u_1$, 방향이 ${\hat{a}}_1$인 벡터가 되고 나머지도 마찬가지기 때문에, 세 개의 축 성분으로 이루어진 벡터 합은 곧 벡터 $\overrightarrow{u}$와 같게 된다.

 

 

이제 좌표계 $\{a\}$의 각축의 성분 $u_1,u_2,u_3$를 다음과 같이 열(column)행렬 형태로 표시하고,

 

$${\mathbf{u}}^a={\left[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}\right]}^T$$

 

${\mathbf{u}}^a$를 '좌표계 $\{a\}$에서의 벡터 $\overrightarrow{u}$의 표현' 이라고 하며 간단히 '벡터 ${\mathbf{u}}^a$' 라고 하기도 한다. 위 식에서 위첨자 $T$는 전치(transpose)를 뜻한다.

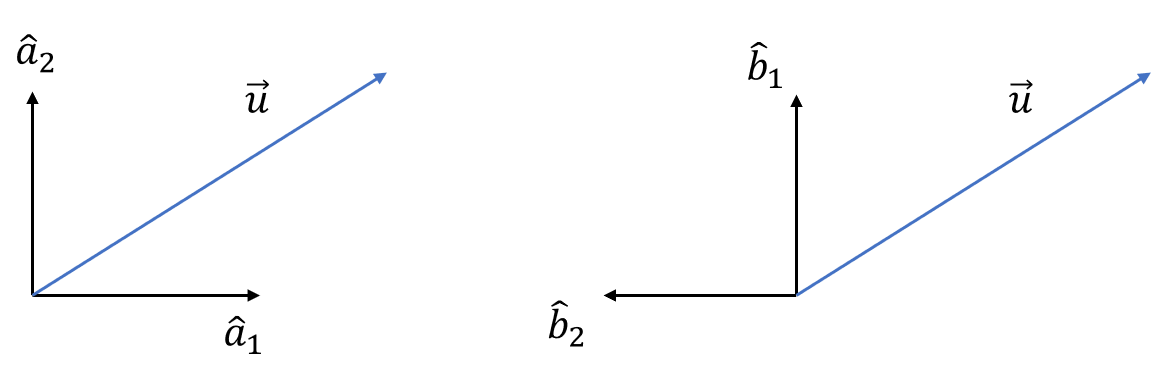
벡터 $\overrightarrow{u}$를 좌표계 $\{b\}$의 축 성분으로 표현할 수도 있다. 좌표계 $\{a\}$와 좌표계 $\{b\}$는 다르기 때문에 동일한 벡터 $\overrightarrow{u}$이라 하더라도 축 성분은 다르게 나올 것이다. 이 경우는 축 성분이 $s_1,s_2,s_3$이다.

 

$$\begin{array}{rl}\overrightarrow{u}& =(\overrightarrow{u}\cdot {\hat{b}}_1){\hat{b}}_1+(\overrightarrow{u}\cdot {\hat{b}}_2){\hat{b}}_2+(\overrightarrow{u}\cdot {\hat{b}}_3){\hat{b}}_3\\ \\ & =s_1{\hat{b}}_1+s_2{\hat{b}}_2+s_3{\hat{b}}_3\end{array}$$

 

 

 

그러면 '좌표계 $\{b\}$에서의 벡터 $\overrightarrow{u}$의 표현'은

 

$${\mathbf{u}}^b={\left[\begin{array}{ccc}{s}_1& s_2& s_3\end{array}\right]}^T$$

 

이다. 이와 같이 보통 같은 벡터라도 좌표계가 달라지면 그 표현이 달라진다. 마치 어떤 과일을 한국 사람은 사과라고 표현하고 미국 사람은 애플이라고 표현하는 것과 마찬가지다.

 

 

한 좌표계에서 표현된 벡터를 다른 좌표계로 표현하려면 좌표변환을 해야 한다. 좌표변환 방법은 몇 가지가 있는데, 많이 사용되는 좌표변환 방식은 3가지다. 방향코사인행렬(DCM, Direction Cosine Matrix), 오일러각(Euler angles), 쿼터니언(Quaternion)이다.