비슷해 보이지만 서로 다른 좌표계가 있다. 경로 좌표계(path coordinate)와 극 좌표계(polar coordinate)이다.
경로 좌표계는 물체가 이동하는 경로를 따라 각 지점에서 물체의 속도 방향(tangential component, \(\hat{e}_t \))과 경로의 곡률 중심(center of curvature) 방향(normal component, \(\hat{e}_n \))을 좌표축으로 삼는다. 그래서 Tangential-Normal 좌표계라고도 한다. 경로가 미리 정해져 있거나 혹은 가늠할 수 있는 경로를 따라 움직이는 물체의 운동을 표현할 때 편리한 좌표계다. 예를 들면 롤러코스터나 자동차 또는 인공위성 등의 운동이 이에 해당한다.
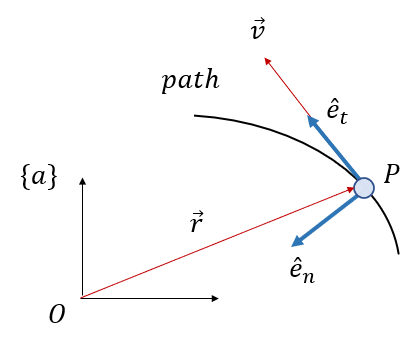
위 그림에서 \(\{a\}\)는 기준 좌표계고 \(O\)는 기준 좌표계의 원점이다. 경로의 접선(tangential) 방향이 곧 물체 \(P\)의 속도 방향이기 때문에 물체의 속도는 다음과 같이 표현할 수 있다.
\[ \vec{v}=v \ \hat{e}_t \]
가속도는 속도 벡터를 기준 좌표계에서 미분한 것이므로 다음과 같이 유도된다.
\[ \begin{align} \vec{a}&= \frac{ ^a d\vec{v}}{dt} \\ \\ &= \frac{dv}{dt} \hat{e}_t + \frac{v^2}{\rho} \hat{e}_n \end{align} \]
여기서 \( \rho \)는 곡률 반경이다. 경로 좌표계는 물체가 경로를 따라 움직일 때 마다 기준 좌표계에 대해서 방향이 계속 바뀐다.
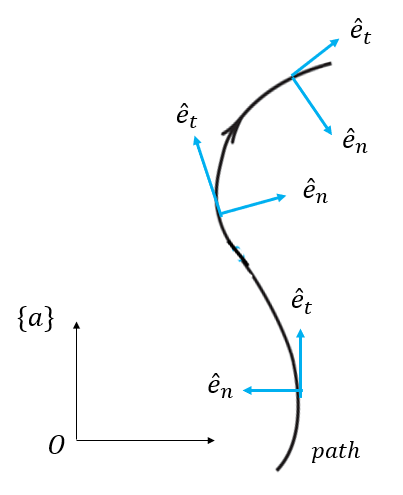
극 좌표계는 기준점에서 물체까지의 거리와 기준축과의 각도인 (\(r, \theta \))를 나타낸다. 이 경우는직교 좌표계가 아니기 때문에, 직교 좌표계인 Radial-Transverse 좌표계를 극 좌표계로 칭하기도 한다.
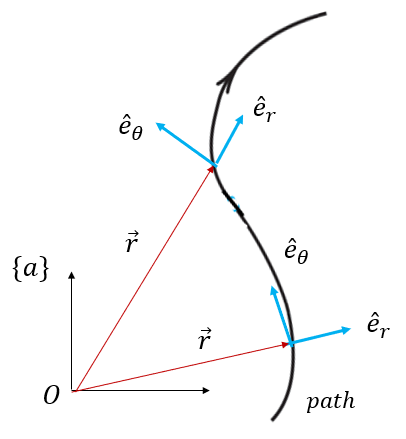
Radial-Transverse 좌표계는 기준점으로부터 물체의 거리와 방향을 측정할 수 있을 때 편리하게 사용될 수 있는 좌표계다. 기준점에서 물체의 위치가 극 좌표점 (\(r, \theta \))로 주어졌을 때, 기준점에서 물체까지의 위치인 방사 방향(radial component, \(\hat{e}_r\))과, 방사 방향과 직각이면서 \(\theta\)가 증가하는 방향(transverse component, \(\hat{e}_\theta \))을 좌표축으로 삼는다.

\(\hat{e}_r\)축은 물체의 위치 벡터 \( \vec{r}\)의 방향은 항상 같기 때문에 위치 벡터는 다음과 같이 표현할 수 있다.
\[ \vec{r} = r \hat{e}_r \]
속도는 위치 벡터를 기준 좌표계에서 미분한 것이므로 다음과 같이 유도된다.
\[ \begin{align} \vec{v}&= \frac{ ^a d\vec{r}}{dt} \\ \\ &= \dot{r} \hat{e}_r + r \dot{\theta} \hat{e}_\theta \end{align} \]
가속도는 속도 벡터를 기준 좌표계에서 미분한 것이므로 다음과 같이 유도된다.
\[ \begin{align} \vec{a}&= \frac{ ^a d\vec{v}}{dt} \\ \\ &= \left( \ddot{r} - r \dot{\theta}^2 \right) \hat{e}_r + \left( r \ddot{\theta} + 2 \dot{r} \dot{\theta} \right) \hat{e}_\theta \end{align} \]
극 좌표계 역시 물체가 경로를 따라 움직일 때 마다 기준 좌표계에 대해서 방향이 계속 바뀐다.
'항공우주 > 동역학' 카테고리의 다른 글
| 오일러각 (Euler Angles) (0) | 2021.02.07 |
|---|---|
| 방향코사인행렬 (DCM) (1) | 2021.02.06 |
| 벡터를 직교 좌표계로 표현하기 (0) | 2021.02.05 |
| 직교 좌표계 (0) | 2021.02.05 |
| 자이로스코프 효과 (1) | 2021.01.10 |




댓글