과학관에 가면 자이로스코프 효과(gyroscopic effect)가 무엇인지 몸으로 느끼게 해주는 장치가 있다. 바로 손잡이가 달려있는 자전거 바퀴와 회전의자다.
처음에는 관람객에게 자전거 바퀴를 양손에 쥐게 한 후 회전의자에 앉힌다. 그리고 회전의자를 돌린다. 그러면 아무런 일도 일어나지 않는다. 이번에는 자전거 바퀴를 손으로 잡아당겨 빠르게 회전시킨다. 그리고 관람객이 앉아 있는 회전의자를 돌린다. 그러면 이번에는 마치 유령이 자전거 바퀴를 비트는 듯한 느낌이 온다. 손으로 꽉 잡지 않으면 자전거 바퀴가 비틀어진다. 매우 신기한 일이다. 이것이 자이로스코프 효과라고 불리는 현상이다.

자이로스코프 효과는 회전하는 물체의 회전축에 모멘트를 가했을 때 모멘트의 회전 방향대로 회전축이 움직이지 않고 그 직각 방향으로 회전하는 현상이다. 언뜻 상식에 반하는 운동처럼 보이지만 사실 뉴턴의 운동법칙을 충실히 만족하는 매우 자연적인 운동이다.
뉴턴의 제2법칙은 질점(particle) 또는 질점으로 간주할 수 있는 물체에 적용된다. 그럼 강체(rigid body)에는 어떻게 적용해야 할까. 강체를 아주 잘게 쪼개서 질점처럼 만들고 각각의 질점에 뉴턴의 법칙을 적용한 후 연속적으로 더하는(적분) 방법을 사용한다. 그러면 두 개의 미분 방정식이 나오는데 하나는 강체의 질량 중심이 마치 질점처럼 병진 운동(translational motion)한다는 방정식이고, 또 하나는 강체가 질량 중심을 중심으로 회전 운동(rotational motion)한다는 방정식이다.
첫번째 병진 운동 방정식은 뉴턴의 제2법칙의 식과 동일하다.
\[ \vec{F} = \frac{^i d\vec{L}}{dt}, \ \ \vec{L} = m\vec{v}_{cm} \]
여기서 \(m\)은 강체의 질량이고, \( \vec{v}_{cm}\)은 강체의 질량 중심의 속도, \(\vec{L}\)은 선형 운동량이다.
두번째 운동방정식은 병진 운동의 회전 운동 버전으로서 다음과 같다.
\[ \vec{M}_{cm} = \frac{^i d\vec{H}_{cm}}{dt}, \ \ \vec{H}_{cm} = \bar{I}_{cm} \cdot ^i \vec{\omega}^b \]
여기서 \(\vec{M}_{cm}\)은 질량 중심을 기준으로 계산한 강체에 작용하는 모멘트이며, \(\bar{I}_{cm}\)은 관성 모멘트 텐서, \(^i \vec{\omega}^b\)는 각속도 벡터, \(\vec{H}_{cm}\)은 질량 중심을 기준으로 계산한 각운동량(angular momentum)이다.
두 식을 보면 서로 유사한 것을 알 수 있다. 힘 \(\vec{F}\)와 모멘트 \(\vec{M}_{cm}\), 선형 운동량 \(\vec{L}\)과 각운동량 \(\vec{H}_{cm}\), 질량 \(m\)과 관성 모멘트 \(\bar{I}_{cm}\), 속도 \(\vec{v}_{cm}\)와 각속도 \(^i \vec{\omega}^b\)는 서로 대응 관계에 있다.
자이로스코프 효과는 회전 운동식을 통해서 설명할 수 있다. 과학관에서 주는 자전거 바퀴는 회전 디스크로 간주할 수 있다.
그러면 회전 디스크의 각운동량 벡터의 크기는 회전축에 관한 관성 모멘트 \(I_0\)(스칼라 값)와 회전축의 각속력 \(\omega_0\)의 곱으로 주어지며, 방향은 오른손 법칙으로 주어지는 회전축 방향(\( \hat{b}_1\))이다. 회전 운동식은 다음과 같이 된다.
\[ \vec{M}_0 = \frac{^i d\vec{H}_0}{dt}, \ \ \vec{H}_0 = \bar{I}_0 \ \omega_0 \ \hat{b}_1 \]
모멘트도 벡터로서 방향은 오른손 법칙에 따른다. 힘 방정식과 마찬가지로 모멘트 방정식에 의하면 강체의 각운동량의 변화율은 그 강체에 가해지는 모멘트와 같고 모멘트의 방향은 각운동량의 '변화' (\(\Delta \vec{H}_0\))방향과 같다.
회전하는 디스크의 회전축에 그림과 같이 짝힘 \(F\) (크기가 같고 방향이 서로 반대인 힘)를 가하면 모멘트(\(\vec{M}_0\))의 방향은 전방 방향이 되고, 뉴턴의 운동법칙에 의해서 모멘트 방향으로 각운동량 벡터의 변화량 \(\Delta \vec{H}_0\)가 생긴다. 따라서 각운동량 벡터는 반시계 방향으로 회전하고 디스크의 회전축도 그 방향으로 회전하게 된다.
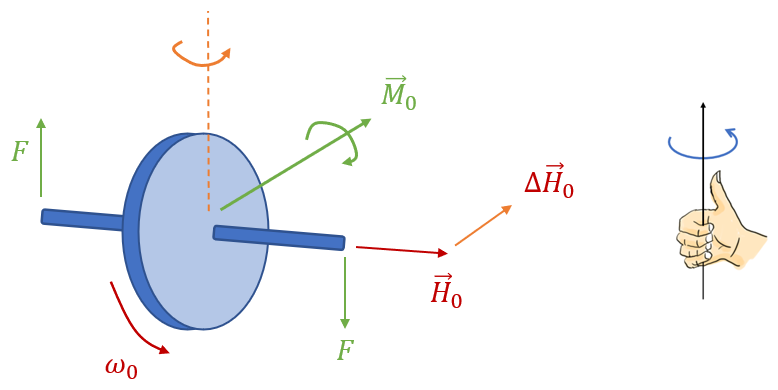
따라서 그림에서 보듯이 디스크의 회전축이 힘을 가한 방향(또는 모멘트의 회전 방향)으로 회전하지 않고 그 직각으로 회전한다. 이를 자이로스코프 효과라고 한다.
다시 과학관의 자전거 바퀴로 돌아와서, 자전거 바퀴를 회전시켜서 각운동량 벡터를 오른쪽으로 향하게 하고, 의자를 반시계 방향으로 회전시키면 위로 향하는 모멘트 벡터가 생긴다. 따라서 바퀴의 각운동량 벡터가 위로 향하는 변화량이 만들어지고 바퀴의 회전축도 위로 들리는 회전이 생기게 되면서 관람객은 자전거 바퀴가 비틀어지는 듯한 느낌을 받게 되는 것이다.
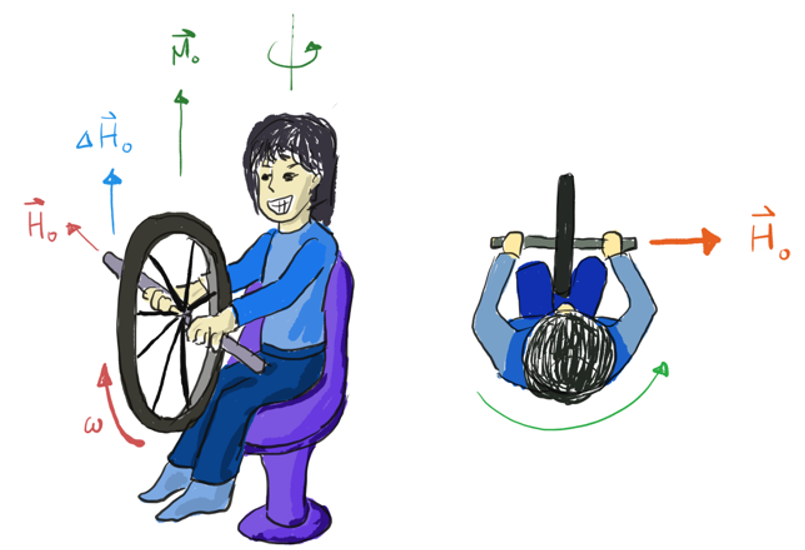
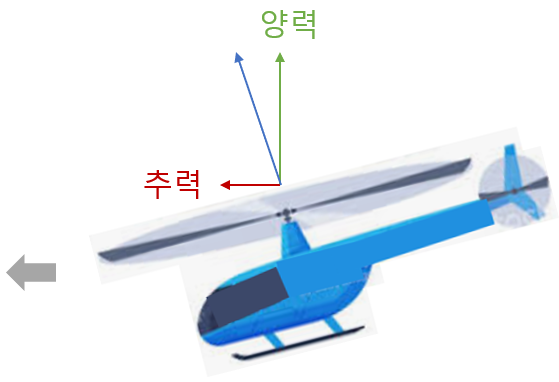
자전거 바퀴 외에 회전 디스크로 간주할 수 있는 것이 여럿 있다. 헬리콥터의 로터도 그렇다. 고정익 항공기는 날개에서 양력을 담당하고 엔진은 추력을 담당한다. 하지만 헬리콥터는 로터가 양력과 추력을 동시에 담당한다. 헬리콥터가 전방으로 이동하려면 로터에서 발생하는 공력 벡터 방향을 전방으로 기울여서 일부를 추력으로 사용해야 한다.
공력 벡터 방향을 전방으로 기울이려면 어떻게 해야 할까. 헬리콥터의 로터 회전축을 기울일 것으로 생각하는 사람이 있는데 그렇지는 않고, 헬리콥터 동체를 앞으로 기울이는 방법을 사용한다.
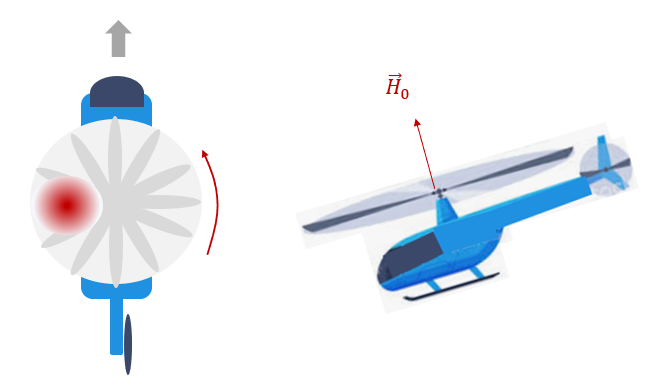
그러면 어떤 방법으로 동체를 앞으로 기울일일 수 있을까. 바로 자이로스코프 효과를 이용한다.
헬리콥터 로터 블레이드의 피치각을 크게 하면 공력이 커지고 반대로 작게 하면 작아진다. 헬리콥터에는 스와시판(swash plate)라는 장치가 있어서 로터 블레이드가 회전하면서 회전 위치에 따라서 피치각을 조정할 수 있다. 언뜻 생각하기에 로터 블레이드가 기체 뒤쪽에 올 때 피치각을 증가시키면 로터 회전면 뒤편에서 공력이 크게 발생하므로 헬리콥터 기체가 앞으로 숙여질 것 같지만 그렇지 않다. 만약 로터 블레이드의 회전 방향이 반시계 방향이라면 로터의 각운동량 벡터는 위로 향해 있으므로, 이 경우에 기체는 왼쪽으로 기울어져서 헬리콥터는 왼쪽으로 날아간다.

전진 비행하려면 로터 블레이드가 헬리콥터 기체 왼편으로 갈 때 피치각을 증가시킨다. 그러면 기체 앞 방향으로 모멘트 벡터가 생기므로 기체가 앞으로 숙여지게 되어 앞으로 비행할 수 있다.
다음 유튜브 영상을 통해서 확인해 보기 바란다.
풍력 터빈의 로터도 회전 디스크로 간주할 수 있다. 흔히 바람 방향이 바뀌면 그 때마다 로터를 바람 방향으로 돌려야 발전 효율이 더 높아질 것으로 생각할 수 있지만 이는 매우 위험한 방법이다. 자이로스코프 효과 때문이다. 풍력 터빈의 로터 블레이드를 전면에서 봤을 때 시계 방향으로 회전한다면 각운동량 벡터는 풍력 터빈 후면으로 향한다. 이 상태에서 풍력 터빈의 전면을 왼쪽으로 회전하려 한다면 모멘트 벡터 방향이 위로 향하게 되므로 자이로스코프 효과에 의해서 터빈의 로터는 아래 방향으로 기울어지게 된다.

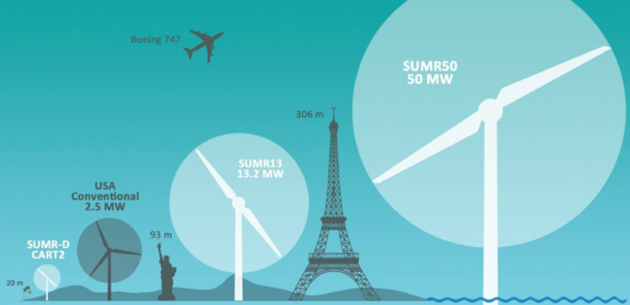
다음 그림은 풍력 터빈의 크기를 보여준다. 매우 큰 구조물이므로 이러한 상황은 아주 위험하기 때문에 풍력 터빈의 방향은 고정시켜 놓거나 아주 천천히 움직이게 한다.
'항공우주 > 동역학' 카테고리의 다른 글
| 오일러각 (Euler Angles) (0) | 2021.02.07 |
|---|---|
| 방향코사인행렬 (DCM) (1) | 2021.02.06 |
| 벡터를 직교 좌표계로 표현하기 (0) | 2021.02.05 |
| 직교 좌표계 (0) | 2021.02.05 |
| 경로 좌표계와 극 좌표계 (0) | 2021.01.09 |




댓글