상단 지점 \((0,0)\)에 정지해 있던 물체가 경로 \(y(x)\)를 따라 마찰없이 중력의 영향으로만 미끄러져서 하단 지점 \((x_f,y_f)\)까지 도착하는데 걸리는 시간은 다음과 같이 계산된다.
\[ t= \int_0^{x_f} \frac{ \sqrt{ 1+ \left( \frac{dy}{dx} \right)^2 } }{ \sqrt{2gy} } \ dx \]
여기서 시간 \(t\)를 최소로 만드는 경로 함수 \(y(x)\)를 계산하는 것이 브라키스토크론(Brachistochrone) 문제다.
시간 \(t\)는 함수 \(y(x)\)를 변수로 하는 functional이다. 이 값을 최소화하는 함수 \(y(x)\)를 찾는 문제이므로 변분법의 문제이다.
다음과 같은 functional \(F(y, y^\prime)\)가 있다고 하자.
\[ F(y, y^\prime)= \int_{x_0}^{x_f} h(y(x),y^\prime (x)) \ dx \]
여기서 \(y(x)\)는 \(x\)의 함수이고, \(y^\prime (x)=\frac{dy}{dx}\)는 \(y(x)\)의 도함수이며, 적분 구간의 양쪽 경계 \(y(0)\)과 \(y(x_f)\)는 고정된 값이다. 변분법의 원리에 의하면 functional \(F(y, y\prime)\)이 (로컬) 최소값을 갖기 위한 필요조건에서 다음과 같은 오일러-라그랑지 방정식이 유도된다.
\[ \frac{ \partial h}{ \partial y} - \frac{d}{dx} \left( \frac{\partial h}{ \partial y^\prime} \right) =0 \]
이제 오일러-라그랑지 방정식을 이용해서 브라키스토크론 문제의 해를 구해보도록 하자. 위 식을 비교해 보면,
\[ h(y, y^\prime) = \frac{ \sqrt{1+(y^\prime )^2}}{ \sqrt{2gy}} \]
이다. 따라서 \(h\)는 명시적으로 \(x\)의 함수가 아니므로,
\[ \frac{ \partial h }{ \partial y^\prime} =c =const \]
이다. 한편,
\[ \begin{align} \frac{ \partial h }{ \partial y^\prime} &= \frac{1}{2} \left( 1+(y^\prime)^2 \right) ^{-\frac{1}{2} } (2 y^\prime) \frac{1}{ \sqrt{2gy}} \\ \\ &= \frac{ y^\prime }{ \sqrt{ (2gy) \left( 1+ (y^\prime)^2 \right) } } \\ \\ &= c \end{align} \]
이다. 위 식은
\[ (y^\prime)^2 = c^2 2gy \left( 1+(y^\prime)^2 \right) \]
이므로, \(y^\prime\)에 관한 식으로 정리하면 다음과 같이 된다.
\[ y^\prime = \frac{dy}{dx}=\sqrt{ \frac{2gc^2y}{ (1-2gc^2y)} } \]
여기서 트릭이 필요하다. 다음과 같이 \(y\)를 새로운 독립변수 \(\theta\)를 도입하여 파라미터화 한다.
\[ y = a (1-\cos \theta ) \]
여기서 \(a\)는 적당한 상수다. \(\theta=0\)일 때 \(y=0\)이 되도록 했다.
위 식의 미분을 구하면,
\[ dy=a \sin \theta \ d\theta = a \sqrt{1-\cos^2 \theta } \ d\theta \]
이므로 \(y^\prime\)에 관한 식에 대입하면 다음과 같이 된다.
\[ \sqrt{ \frac{ 1-2gc^2a (1-\cos \theta ) }{2gc^2a (1-\cos \theta ) } } a \sqrt{1-\cos^2 \theta } \ d\theta = dx \]
이제 식을 단순화하기 위해서 이제 상수 \(a\)를 다음과 같이 정한다.
\[ a= \frac{1}{4gc^2} \]
그러면, 위 식은 다음과 같이 단순하게 바뀐다.
\[ a(1+\cos\theta ) \ d\theta =dx \]
위 식을 적분하면 \(x\)를 구할 수 있다. 마찬가지로 \(\theta=0\)일 때 \(x=0\)이 되도록 했다.
\[ x=a ( \theta - \sin \theta ) \]
결국 브라키스토크론 문제의 해는 다음과 같이 \(\theta\)로 파라미터화된 함수로 구할 수 있다.
\[ \begin{align} x &= a(\theta - \sin \theta ) \\ \\ y &= a(1-\cos \theta ) \end{align} \]
도착 지점인 하단 지점 \((x_f, y_f )\)가 주어지면, 위 식을 이용해서 \(a\)와 \(\theta \)는 항상 구할 수 있다(비록 어렵지만 ...).
예를 들어서 상단 지점 \((0, 0)\)에서 하단 지점 \((10, 5)\)미터까지 최단 시간 이동 경로를 구해보자. 먼저 \(a\)와 \(\theta_f\)를 계산하면 다음과 같다.
\[ \begin{align} & a=2.586 \\ \\ & \theta_f=3.5083646 \ rad \end{align} \]
최단 시간 이동 경로의 그림은 다음과 같다.
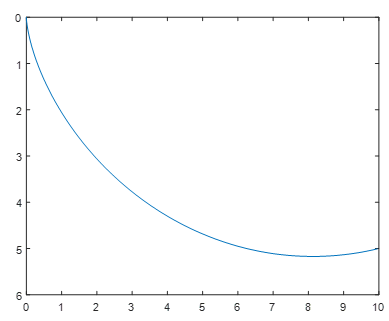
그럼 이 경로로 움직였을 때 이동 시간은? 원래 적분 식을 풀어야 되는데, 어렵기 때문에 일단 패스하고, 나중에 최적제어 알고리즘을 이용해서 시간을 계산해 보기로 하자.
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-2] 르장드르 다항식 (Legendre Polynomials) (0) | 2021.12.15 |
|---|---|
| [PSOC-1] 유사 스펙트럴 기반 최적제어 개요 (0) | 2021.12.15 |
| 변분법과 오일러-라그랑지 방정식 (0) | 2021.01.12 |
| 변분법 (calculus of variation) (0) | 2021.01.11 |
| 브라키스토크론 문제와 변분법 (0) | 2021.01.08 |




댓글