[B-Plane] B-평면 타켓팅 - 1

B-평면 타겟팅(B-plane targeting)은 우주 탐사에서 행성 플라이바이(flyby)나 행성의 접근 경로를 설계할 때 사용되는 중요한 개념이다. B-평면 타켓팅의 목표는 B-평면 상에서 특정 목표점을 맞추는 것이며 이 과정을 통해서 행성 플라이바이, 궤도 진입 (orbit insertion) 또는 행성 착륙 목표 지점 타겟팅의 조건을 만족시킬 수 있다.

또한 행성 간 임무를 수행하는 동안 우주비행체는 섭동력의 영향을 받아 궤도가 원하는 임무 궤도에서 벗어날 수 있으므로 현재 우주비행체의 상태벡터와 목표점 좌표를 바탕으로 오차를 보정하기 위한 궤적수정기동(TCM, trajectory correction manuever)을 설계하는 데에도 B-평면 타겟팅을 적용할 수 있다.

먼저 B-평면 타켓팅과 관련하여 유용한 3가지 알고리즘을 소개한다.
첫번째 알고리즘은 쌍곡선 초과속도(hyperbolic excess velocity) 벡터 \(\vec{v}_\infty\), 설계자가 목표로 하는 근지점(periapsis 또는 perigee)까지의 거리 \(r_p\) 및 궤도의 경사각 \(i\) 가 입력으로 주어졌을 때, B-평면 파라미터를 계산하고 이를 기반으로 도착 쌍곡선 궤도를 결정하는 알고리즘이다. 이 알고리즘을 이용하면 B-평면 타겟팅을 위한 조준점(aim point)을 설정할 수 있다. 여기서 쌍곡선 초과속도 벡터는 행성간 비행단계의 결과로 얻어진다. 알고리즘은 다음과 같다.

0. 입력: \(\vec{v}_\infty, \ r_p, \ i\)

1. \(\vec{v}_\infty\) 로 부터 B-평면 좌표축 \(\hat{S}, \hat{R}, \hat{T}\) 을 계산한다.

            \( \hat{S} = \frac{\vec{v}_\infty}{ \vert \vec{v}_\infty \vert }, \ \ \ \ \ \hat{T}= \frac{ \hat{S} \times \hat{N} }{ \vert \hat{S} \times \hat{N} \vert }, \ \ \ \ \ \hat{R}= \hat{S} \times \hat{T} \)

2. \(\hat{S}\) 으로부터 적경 (RA, right ascension) \(\alpha_\infty\) 과 적위 (Dec, declination) \(\delta_\infty\) 를 계산한다.

            \(\alpha_\infty = \tan^{-1} \frac{S_y}{S_x}, \ \ \ \ \ \delta_\infty = \sin^{-1}⁡ S_z \)

3. \(r_p, \ i\) 로 부터 \(B\) 와 \(\phi \) 를 계산한다.

            \(B=r_p \sqrt{1+ \frac{2\mu}{v_\infty^2 r_p } } \)
            \( \cos (-\phi) = \frac{ \cos i}{\cos \delta_\infty } \)

여기서 위 식에 의하면,

 

\[ \vert \cos (-\phi) \vert = \lvert \frac{ \cos i}{ \cos \delta_\infty } \rvert \le 1 \]

 

이므로 \( \vert \cos \delta_\infty \vert \ge \vert \cos i \vert\) 또는 \(\vert \sin \delta_\infty \vert \le \vert \sin i \vert\) 을 만족해야 한다. 즉 \(\vert \delta_\infty \vert \le \vert i \vert \) 이어야 하므로 궤도의 경사각은 진입 점근선의 적위보다 크거나 같게 설정해야 한다.

4. \(B\) 와 \(\phi\) 로 부터 \(B_T, \ B_R\) 및 B-벡터를 계산한다.

            \( B_T=B \cos \phi, \ \ \ \ \ B_R=B \sin \phi \)
            \( \vec{B}=B_T \hat{T}+B_R \hat{R} \)

5. 도착 쌍곡선 궤도 파라미터를 계산한다.

      5-1. 에너지와 장반경 \(a\) 계산

            \( \mathcal{E} = \frac{ v_\infty^2 }{2}=- \frac{\mu}{2a} \)

      5-2. 이심율 계산

            \( e=1- \frac{r_p}{a} \)

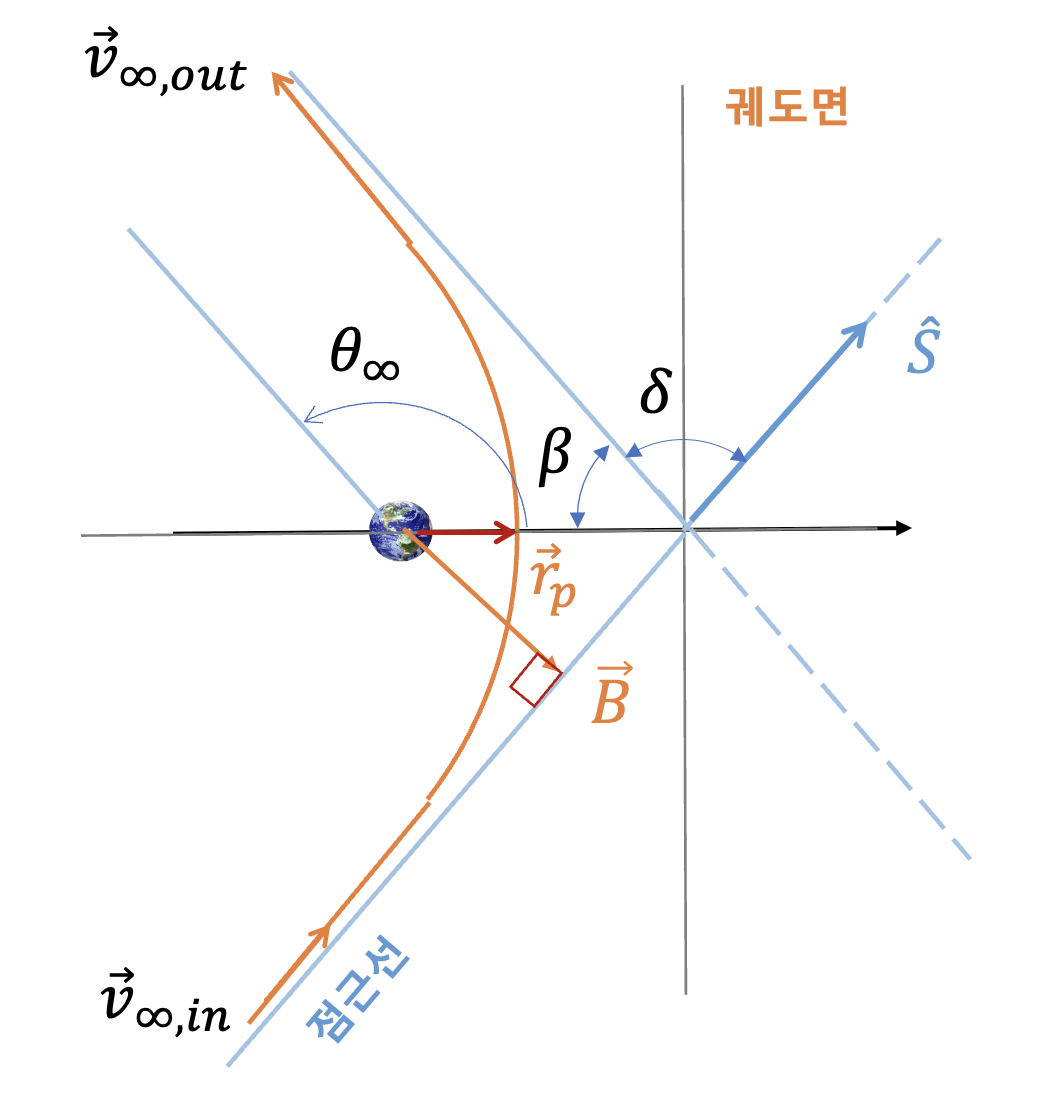
      5-3. 무한대에서 실제비행각 계산

            \( \theta_\infty = \cos^{-1} \left(- \frac{1}{e} \right) \)

      5-4. 점근선의 각도 \(\beta\) 및 회전각 \(\delta\) 계산

            \( \beta= \cos^{-1} \left( \frac{1}{e} \right), \ \ \ \ \ \delta=2 \sin^{-1} \left( \frac{1}{e} \right) \)

 

 

다음은 이 알고리즘의 매트랩 코드다.

 

vri2bplane.m

 

function [bplane, hyper] = vri2bplane(vinf_vec, rp, i, mu)
%
% [bplane, hyper] = vri2bplane(vinf_vec, rp, i, mu)
% input
%   vinf_vec: excessive velocity vector wrt target planet
%   rp : perigee
%   i: inclination
%   mu: gravitational parameter of target planet (km^3/s^2)
%       Mars - 42 828
%       Venus - 324 900
%       Moon - 4903
%       Earth - 398 600
%
% output
%   bplane.S_hat: incoming asymptote vector
%   bplane.T_hat: B-plane axis
%   bplane.R_hat: 
%   bplane.B_vec: B-vector
%   bplane.BT: impact parameter (km)
%   bplane.BR
%   bplane.phi: B-vector angle (rad)
%
%   hyper.vinf: excessive velocity (km/s)
%   hyper.RA (rad)
%   hyper.Dec
%   hyper.a: SMA
%   hyper.e: ECC
%   hyper.rp: perigee
%   hyper.the_inf: true anomaly at inifinity
%   hyper.delta: turn angle
%   hyper.beta: asymptote angle
%
% (c) st.watermelon

% 1. B-plane axes
vinf = norm(vinf_vec);
S_hat = vinf_vec/vinf;
N_hat = [0 0 1]';
T_hat = cross(S_hat, N_hat);
T_hat = T_hat/norm(T_hat);
R_hat = cross(S_hat, T_hat);

% 2. asymptote RA and Dec
RA = atan2(S_hat(2), S_hat(1));
Dec = asin(S_hat(3));

% 3. B-plane paramters
B = rp*sqrt(1+2*mu/(vinf^2*rp));
phi = -acos(cos(i)/cos(Dec));
if Dec<0
    phi = -phi;
end

% 4. B-vector
BT = B*cos(phi);
BR = B*sin(phi);

B_vec = BT*T_hat + BR*R_hat;

% 5. hyperbolic parameters
% 5-1. energy and SMA
E = vinf^2/2;
a = -mu/(2*E);

% 5-2. eccentricity
e = 1-rp/a;

% 5-3. true anomaly at inifinity
the_inf = acos(-1/e);

% 5-4. turn angle and asymptote angle
delta = 2*asin(1/e);
beta = acos(1/e);



%%
% output

bplane.S_hat = S_hat;
bplane.T_hat = T_hat;
bplane.R_hat = R_hat; 
bplane.B_vec = B_vec;
bplane.BT = BT;
bplane.BR = BR;
bplane.phi = phi;

hyper.vinf = vinf;
hyper.RA = RA;
hyper.Dec = Dec;
hyper.a = a;
hyper.e = e;
hyper.rp = rp;
hyper.the_inf = the_inf;
hyper.delta = delta;
hyper.beta = beta;

 

 

 

첫번째 알고리즘이 목표로 하는 B-평면 파라미터를 계산하는 것이었다면, 두번째 알고리즘은 실제 우주비행체의 위치벡터 \(\vec{r}\) 과 속도벡터 \(\vec{v}\) 를 이용하여 B-평면과 쌍곡선궤도의 파라미터를 계산하는 알고리즘이다.

0. 입력 \(\vec{r}, \ \vec{v}\)

1. \(\vec{r}\) 와 \(\vec{v}\) 로 부터 각운동량벡터 \(\vec{h}\) 와 이심율벡터 \(\vec{e}\) 를 계산한다.

            \( \vec{h}= \vec{r} \times \vec{v}, \ \ \ \ \ \vec{e}= \frac{1}{\mu} \left( \vec{v} \times \vec{h}- \mu \frac{ \vec{r}}{r} \right) \)

2. 쌍곡선 초과속도 \(v_\infty\) 를 계산한다.

            \( v_\infty = \sqrt{ v^2- \frac{ 2 \mu}{r} } \)

3. 장반경 \(a\) 와 경사각 \(i\) 를 계산한다.

            \( \mathcal{E} = \frac{v_\infty^2 }{2} =- \frac{\mu}{2a} , \ \ \ \ \ \cos i= \frac{ \hat{N} \cdot \vec{h}}{h} \)

4. 실제비행각과 근지점을 계산한다.

            \( \cos \theta = \frac{ \vec{e} \cdot \vec{r}}{er}, \ \ \ \ \ r_p=a(1-e) \)

5. 최근접 도달 시간(TCA)을 계산한다.

            \( \tanh\frac{F}{2} = \sqrt{ \frac{e-1}{e+1} } \tan \frac{\theta}{2} \)
            \( t_{TCA}= \sqrt{ \frac{(-a)^3}{\mu} } (F-e \sinh F ) \)

6. 무한대에서 실제비행각을 계산한다.

            \( \theta_\infty = \cos^{-1} (- \frac{1}{e} ) \)

7. 점근선의 각도 \(\beta\) 및 회전각 \(\delta\) 를 계산한다.

            \( \beta =\cos^{-1} ( \frac{1}{e} ), \ \ \ \ \ \delta =2 \sin^{-1} ( \frac{1}{e}) \)

8. B-평면 좌표축 \(\hat{S}, \ \hat{R}, \ \hat{T}\) 을 계산한다.

            \( \hat{S}= \frac{\vec{e}}{e^2} + \frac{ \sqrt{e^2-1} }{e^2} \frac{ \vec{h} \times \vec{e} }{h} \)
            \( \hat{T}= \frac{ \hat{S} \times \hat{N} }{ \vert \hat{S} \times \hat{N} \vert }, \ \ \ \ \ \hat{R}= \hat{S} \times \hat{T} \)

9. \( \vec{B}\) 를 계산한다.

            \( \vec{B}= \frac{ \hat{S} \times \vec{h} }{v_\infty } \)
            \( B_T= \vec{B} \cdot \hat{T}, \ \ \ \ \ B_R= \vec{B} \cdot \hat{R} \)
            \( \tan \phi= \frac{B_R}{B_T} \)

10. \(\hat{S}\) 으로부터 적경 (RA, right ascension) \(\alpha_\infty\) 과 적위 (Dec, declination) \(\delta_\infty\) 를 계산한다.

            \( \alpha_\infty = \tan^{-1} \frac{S_y}{S_x}, \ \ \ \ \ \delta_\infty= \sin^{-1} S_z \)

다음은 이 알고리즘의 매트랩 코드다.

 

rv2bplane.m

 

function [bplane, hyper] = rv2bplane(r_vec, v_vec, mu)
%
% [bplane, hyper] = rv2bplane(r_vec, v_vec, mu)
% input
%   r_vec, v_vec : position and velocity vector (km, km/s) wrt target
%   mu: gravitational parameter of target planet (km^3/s^2)
%       Mars - 42 828
%       Venus - 324 900
%       Moon - 4903
%       Earth - 398 600
%
% output
%   bplane.S_hat: incoming asymptote vector
%   bplane.T_hat: B-plane axis
%   bplane.R_hat: 
%   bplane.B_vec: B-vector
%   bplane.BT: impact parameter (km)
%   bplane.BR
%   bplane.phi: angle (rad)
%
%   hyper.vinf: excessive velocity (km/s)
%   hyper.RA (rad)
%   hyper.Dec
%   hyper.a: SMA
%   hyper.e: ECC
%   hyper.i: inclination
%   hyper.the: true anomaly
%   hyper.rp: perigee
%   hyper.tca: time to closest approachs (sec)
%   hyper.the_inf: true anomaly at inifinity
%   hyper.delta: turn angle
%   hyper.beta: asymptote angle
%
% (c) st.watermelon


% 1. angluar momentum and eccentricity
r = norm(r_vec);
v = norm(v_vec);

h_vec = cross(r_vec, v_vec);
h = norm(h_vec);

e_vec = cross(v_vec, h_vec)/mu - r_vec/r;
e = norm(e_vec);

% 2. hyperbolic excessive velocity
vinf = sqrt(v^2-2*mu/r);

% 3. SMA and inlination
E = vinf^2/2;
a = -mu/(2*E);
i = acos([0 0 1]*h_vec/h);  

% 4. true anomaly and perigee
the=acos(e_vec'*r_vec/(e*r));
if (r_vec'*v_vec<0) the = -the; end

rp = a*(1-e);

% 5. TCA
tmp = sqrt((e-1)/(e+1))*tan(the/2);
F = 2*atanh(tmp);
tca = sqrt((-a)^3/mu)*(F-e*sinh(F));

% 6. true anomaly at infinity
the_inf = acos(-1/e);

% 7. asymptote angle and turn angle
beta = acos(1/e);
delta = 2*asin(1/e);

% 8. B-plane axes
S_hat = e_vec/e^2 + sqrt(e^2-1)/e^2 * cross(h_vec, e_vec)/h;
N_hat = [0 0 1]';
T_hat = cross(S_hat, N_hat);
T_hat = T_hat/norm(T_hat);
R_hat = cross(S_hat, T_hat);

% 9. B-vector
B_vec = cross(S_hat, h_vec)/vinf;
BT = B_vec'*T_hat;
BR = B_vec'*R_hat;

phi = atan2(BR, BT);

% asymptote RA and Dec
RA = atan2(S_hat(2), S_hat(1));
Dec = asin(S_hat(3));

% output

bplane.S_hat = S_hat;
bplane.T_hat = T_hat;
bplane.R_hat = R_hat; 
bplane.B_vec = B_vec;
bplane.BT = BT;
bplane.BR = BR;
bplane.phi = phi;

hyper.vinf = vinf;
hyper.RA = RA;
hyper.Dec = Dec;
hyper.a = a;
hyper.e = e;
hyper.i = i;
hyper.the = the;
hyper.rp = rp;
hyper.tca = tca;
hyper.the_inf = the_inf;
hyper.delta = delta;
hyper.beta = beta;

 

 

 

세번째는 플라이바이 또는 중력도움(gravity assist) 비행에 유용한 알고리즘으로서 진입과 진출 쌍곡선 초과속도 벡터인 \(\vec{v}_{\infty,in}\) 과 \(\vec{v}_{\infty,out}\) 이 주어졌을 때, B-벡터와 근지점 거리 \(r_p\) 를 구하는 알고리즘이다.

0. 입력 \( \vec{v}_{\infty,in}, \ \vec{v}_{\infty,out} \)

1. \(\vec{v}_{\infty,in}\) 로 부터 \(\hat{S}\) 를 계산한다.

            \( \hat{S}= \frac{ \vec{v}_{\infty,in} }{ \vert \vec{v}_{\infty,in} \vert } \)

2. \(\vec{v}_{\infty,in}\) 와 \(\vec{v}_{\infty,out}\) 로 부터 \(\hat{h}\) 을 계산한다. \(\hat{h}\) 은 \(\vec{h}\) 와 같은 방향을 갖는 단위벡터다.

            \( \hat{h}= \frac{ \vec{v}_{\infty,in} \times \vec{v}_{\infty,out} }{ \vert \vec{v}_{\infty,in} \times \vec{v}_{\infty,out} \vert } \)

3. \(\hat{R}, \ \hat{T}\) 과 \(\hat{B}\) 을 계산한다. \(\hat{B}\) 은 B-백터와 같은 방향을 갖는 단위벡터다.

            \( \hat{T}= \frac{ \hat{S} \times \hat{N} }{ \vert \hat{S} \times \hat{N} \vert }, \ \ \ \ \ \hat{R}= \hat{S} \times \hat{T} \)
            \(\hat{B} = \hat{S} \times \hat{h} \)

4. 진입(incoming) 점근선과 진출(outgoing) 점근선 사이의 각도인 회전각(turn angle) \(\delta\) 를 계산한다.

            \( \cos \delta= \frac{ \vec{v}_{\infty,in} \cdot \vec{v}_{\infty,out} }{ \vert \vec{v}_{\infty,in} \vert \ \vert \vec{v}_{\infty,out} \vert } \)

5. 점근선의 각도 \(\beta\) 와 이심율 \(e\) 를 계산한다.

            \( \beta= \frac{\pi-\delta }{2}, \ \ \ \ \ \cos \beta =\frac{1}{e} \)

6. \(r_p\) 를 계산한다.

            \( e=1+ \frac{r_p v_\infty^2}{\mu} \ \ \ \ \ \to \ \ \ r_p = \frac{ \mu}{ \vert \vec{v}_{\infty,in} \vert ^2 } (e-1) \)

7. \( \vec{B}\) 를 계산한다.

            \( B= \frac{ \mu }{ \vert \vec{v}_{\infty,in} \vert ^2 } \sqrt{e^2-1} \)
            \( \vec{B}=B \ \hat{B} \)