B-평면과 관련하여 3개의 평면을 정의할 수 있다. 목표(target) 행성의 적도면(equatorial plane), 진입 궤도면(orbital plane), 그리고 B-평면(B-plane)이 그것이다. 또한 각 평면에서 각각 행성중심관성좌표계 \(\{a\}\), 궤도중심좌표계(perifocal frame) \(\{p\}\), 그리고 TRS좌표계 \(\{s\}\) 를 정의할 수 있다. 아래 그림에 이 3개의 평면과 좌표계가 나와 있다. 그림에서 \(i\) 는 궤도의 경사각, \(\vec{h}\) 는 각운동량 벡터다.
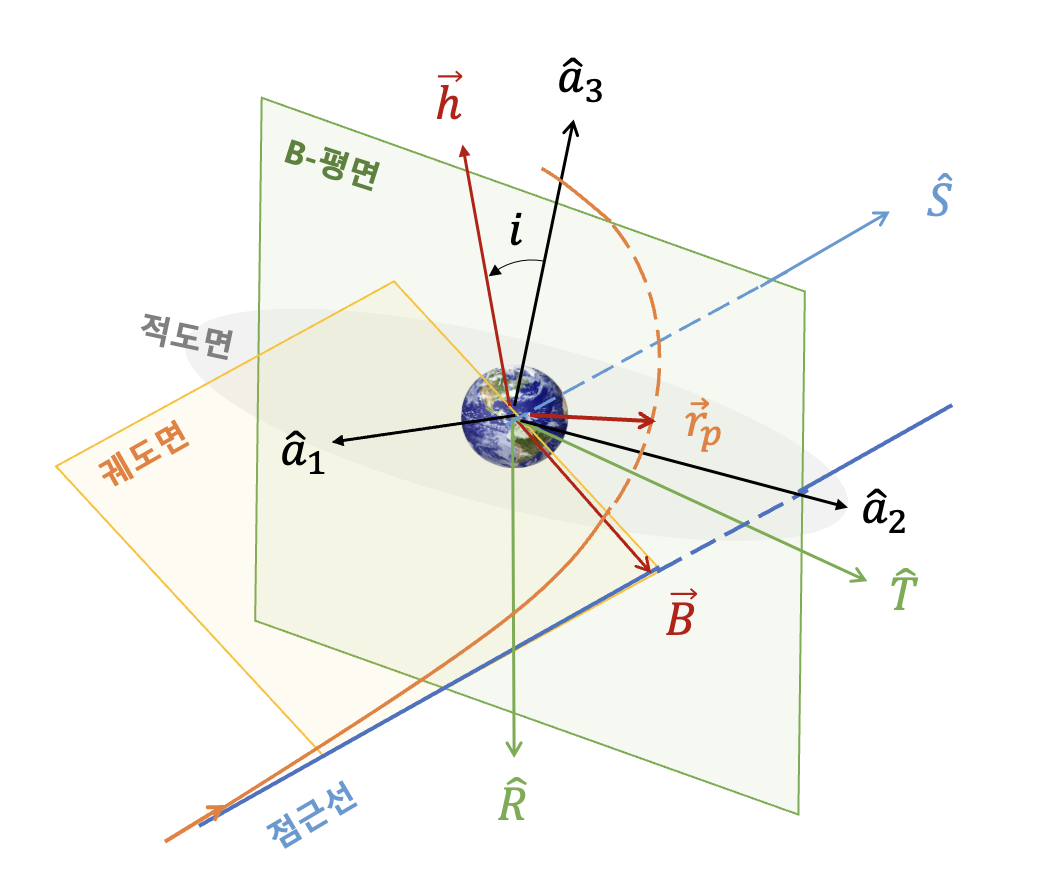
TRS좌표계 \(\{s\}\) 는 행성의 중심에 원점이 있고 점근선벡터 \(\hat{S}\) 를 z축, \(\hat{T}\) 을 x축, \(\hat{R}\) 을 y축으로하는 좌표계다. 관성좌표계 상에서 진입 점근선 벡터의 방향은 다음과 같이 적경(RA, right ascension) \(\alpha_\infty\) 과 적위 (Dec, declination) \(\delta_\infty\) 로 나타낼 수 있다.
\[ \begin{align} \alpha_\infty &= \tan^{-1} \frac{S_y}{S_x} \tag{1} \\ \\ \delta_\infty &= \sin^{-1} S_z \end{align} \]
여기서 \( S_x, \ S_y, \ S_z\) 는 \(\hat{S}\) 의 관성좌표계 축성분이다.

이 두 각을 이용하면 관성좌표계에서 TRS좌표계로의 DCM \(C_s^a\) 를 다음과 같이 단계적으로 계산할 수 있다. 먼저 관성좌표계의 z축을 중심으로 \(-(90^0-\alpha_\infty)\) 만큼 회전한 후,

회전된 좌표계의 x축 (그림에서 \(\hat{a}_1^\prime \))을 중심으로 \(-(90^0-\delta_\infty)\) 만큼 회전한다.

그러면 관성좌표계의 z축은 \(\hat{S}\) 으로, x축은 \(\hat{T}\) 으로, y축은 \(\hat{R}\) 로 이동하여 정렬하게 된다. 이를 DCM으로 표현하면 다음과 같다.
\[ \begin{align} C_s^a &= C(z,-(90^0-\alpha_\infty ) ) \ C(x,-(90^0-\delta_\infty )) \tag{2} \\ \\ &= \begin{bmatrix} \sin \alpha_\infty & \cos \alpha_\infty & 0 \\ -\cos \alpha_\infty & \sin \alpha_\infty & 0 \\ 0 & 0 & 1 \end{bmatrix} \ \begin{bmatrix} 1 & 0 & 0 \\ 0 & \sin \delta_\infty & \cos \delta_\infty \\ 0 & - \cos \delta_\infty & \sin \delta_\infty \end{bmatrix} \end{align} \]
위와 같은 좌표변환에 의하면 \(\hat{T}\) 축은 행성의 적도면에도 존재한다.

궤도중심좌표계 \(\{p\}\) 는 행성의 중심에 원점이 있고, 근지점 방향을 x축, 각운동량 벡터를 z축으로 하는 좌표계다.

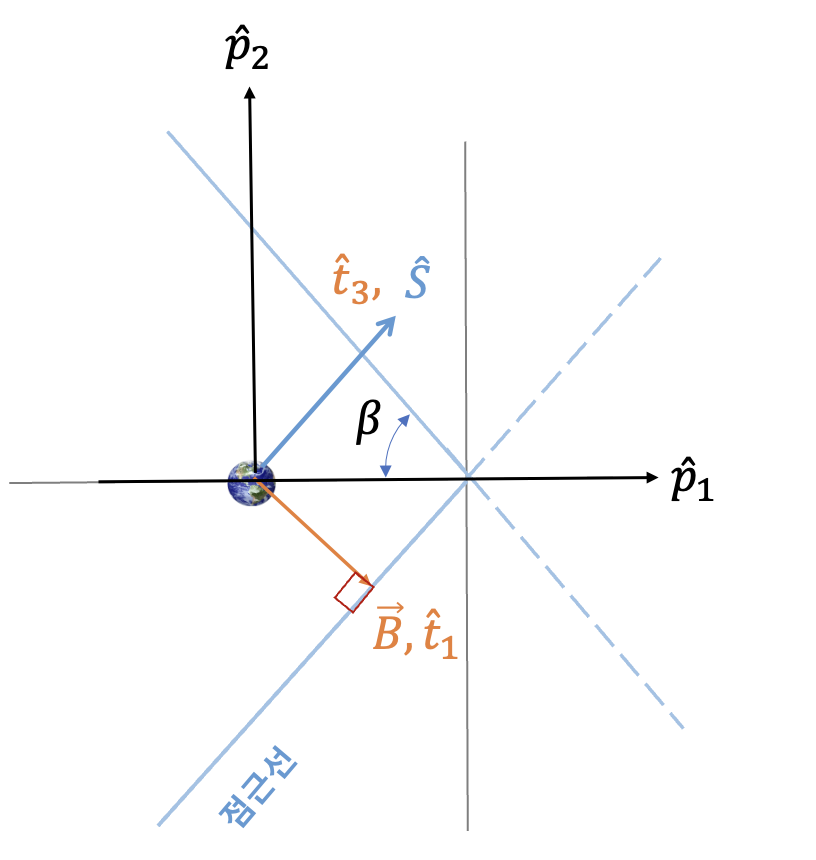
정의에 의하면 B-벡터는 궤도면과 B-평면상에 동시에 존재하므로 TRS좌표계와 궤도중심좌표계의 관계식을 계산하기 전에 먼저 TRS좌표계의 z축인 \(\hat{S}\) 를 중심으로 \(\phi\) 만큼 회전하여 \(\hat{T}\) 축을 B-벡터 뱡향과 일치시키는 좌표변환이 필요하다. 이 좌표계를 임시 좌표계 \(\{t\}\) 라고 하면 TRS좌표계에서 임시 좌표계로의 DCM \(C_t^s\) 는 다음과 같다.
\[ \begin{align} C_t^s = \begin{bmatrix} \cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{3} \end{align} \]
이제 점근선 각 \(\beta\) 와 DCM의 정의에 의해서 임시 좌표계에서 궤도중심좌표계로의 DCM을 구하면 다음과 같다.
\[ \begin{align} C_t^p &= \begin{bmatrix} \cos (90^0-\beta) & - \cos \beta & 0 \\ 0 & 0 & -1 \\\ \cos \beta & \cos (90^0-\beta) & 0 \end{bmatrix} \tag{4} \\ \\ &= \begin{bmatrix} \sin \beta & -\cos \beta & 0 \\ 0 & 0 & -1 \\ \cos \beta & \sin \beta & 0 \end{bmatrix} \end{align} \]
식 (2) 와 (3), (4)를 이용하면 최종적으로 행성중심관성좌표계에서 궤도중심좌표계로의 DCM \(C_p^a\) 를 계산할 수 있다.
\[ \begin{align} C^a_p = C^a_s C^s_t C^t_p \tag{5} \end{align} \]
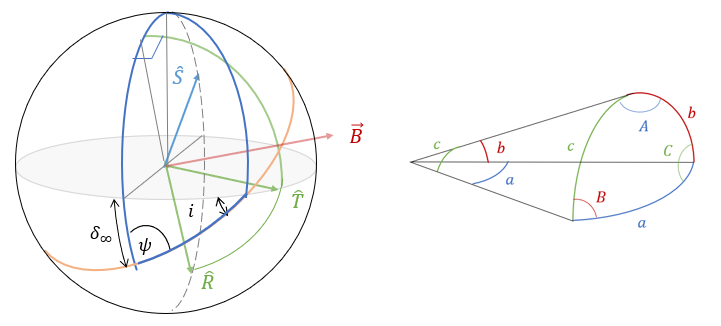
이제 궤도의 경사각 \(i\), \(\hat{T}\) 과 \(\vec{B}\) 의 사잇각 \(\phi\), 그리고 \(\hat{S}\) 의 적위 \(\delta_\infty\) 사이의 관계식을 알아보자. 다음 그림에 3개의 평면과 \(i, \ \phi, \ \delta_\infty\) 가 도시되어 있다. 매우 복잡하게 보이지만 오른쪽 그림에 나온 3개 각의 정의와 비교해 보면 이해가 갈 것이다.

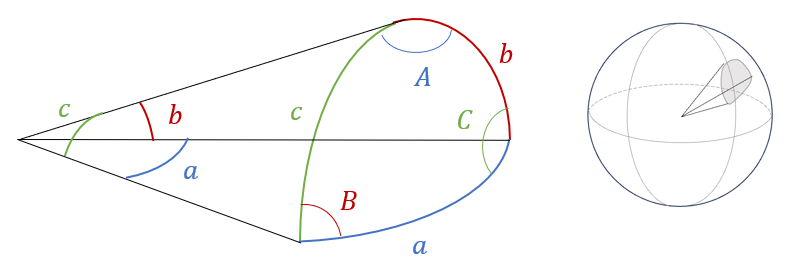
구면(sphere) 사인법칙 (https://pasus.tistory.com/319)을 적용하면 3개의 각사이에 어떤 관련이 있는지 식으로 나타낼 수 있다. 구면 사인법칙은 다음과 같이 구면 상에 정의된 각사이에 다음 수식이 성립한다는 법칙이다.
\[ \begin{align} \frac{\sin a}{\sin A}= \frac{\sin b}{\sin B} = \frac{\sin c}{\sin C} \tag{6} \end{align} \]
아래 그림과 같이 적절하게 구면 삼각형을 선택하고 오른쪽 그림과 비교해보면, \( B \to \psi, \ C \to 90^0, \ b \to 90^0-(-\phi), \ c=90^0\) 의 관계가 있다는 것을 알 수 있다.

이를 식 (6)에 대입하면 다음과 같이 된다.
\[ \begin{align} & \frac{\sin (90^0-(-\phi))}{\sin \psi} = \frac{\sin 90^0 }{\sin 90^0} \\ \\ \to & \ \cos \phi= \sin \psi \tag{7} \end{align} \]
또 다른 구면 삼각형을 선택한 후, 오른쪽 그림과 비교해보면 이번에는 \(B \to \psi, \ C \to 90^0+i, \ b \to 90^0 \ c=90^0+\delta_\infty \) 의 관계가 있다는 것을 알 수 있다.
이를 식 (6)에 대입하면 다음과 같이 된다.
\[ \begin{align} & \frac{\sin 90^0 }{\sin \psi} = \frac{ \sin (90^0+ \delta_\infty )}{\sin (90^0+i)} \\ \\ \to & \ \frac{1}{\sin \psi} = \frac{\cos \delta_\infty}{\cos i} \tag{8} \end{align} \]
식 (7)을 (8)에 대입하면 다음과 같은 관계식을 얻을 수 있다.
\[ \begin{align} \cos (-\phi)= \frac{\cos i}{\cos \delta_\infty} \tag{9} \end{align} \]
식 (9)에 의하면 세 각 \(i, \ \phi, \ \delta_\infty\) 는 서로 독립적이지 않고 함수 관계에 있다는 것을 알 수 있다.
'항공우주 > 우주역학' 카테고리의 다른 글
| [B-Plane] B-평면 타켓팅 - 2 (0) | 2025.01.31 |
|---|---|
| [B-Plane] B-평면 타켓팅 - 1 (0) | 2025.01.30 |
| [B-Plane] B-평면의 정의 (0) | 2024.12.30 |
| 쌍곡선 궤도의 기하학 (0) | 2024.12.27 |
| 대기 항력에 의한 궤도요소의 시간 변화율 (0) | 2024.10.29 |




댓글