[B-Plane] B-평면의 정의

우주비행체가 목표로 한 도착지 행성의 중력권으로 접근하는 단계에서의 궤도 설계는 행성의 궤도에 진입할지 또는 플라이바이(fly-by) 기동을 할지 등, 임무 목적에 따라 달라지며 이와 관련하여 설정된 조건의 충족을 목표로 삼아 수행된다.

예를 들어 행성의 궤도에 진입하는 것을 목적으로 할 경우 특정 시간에 특정 고도, 특정 경사각을 가진 궤도의 지점으로 도착해야 한다는 목표를 설정할 수 있을 것이다. 이러한 목표를 도착 타겟팅이라고 한다. 도착 타겟팅은 도착지 행성을 기준으로 진입 점근선(incoming asymptote)을 원하는 위치와 방향으로 배치하는 것으로써 달성될 수 있는데 이 때 사용되는 유용한 방법이 B-평면 타켓팅(B-plane targeting)이다.

B-평면은 점근선의 위치와 방향을 단순하게 '평면의 조준점'으로 표현할 수 있을 뿐 아니라 섭동력이 궤적에 미치는 영향과 궤적 추정의 불확실성 등을 쉽게 매핑할 수 있다. 또한 조준점과 우주비행체의 속도벡터와의 관계식을 이용하면 속도벡터의 조정으로 수행되는 궤적수정기동(TCM, trajectory correction manuever) 설계에도 쉽게 적용할 수 있다.

 

 

B-평면은 아래 그림과 같이 목표로 하는 도착지 행성의 중심을 원점으로 하고 진입 점근선과 수직인 평면으로 정의한다. 그림에서 $\hat{S}$ 는 점근선벡터(asymptote vector)로서 진입 점근선의 방향을 나타내는 단위벡터다. 이 벡터는 점근선과 평행하므로 우주비행체의 쌍곡선 초과속도(hyperbolic excess velocity) 벡터인 ${\overrightarrow{v}}_{\mathrm{\infty }}$ 와도 평행하다. 두 벡터 $\hat{S}$ 와 ${\overrightarrow{v}}_{\mathrm{\infty }}$ 는 궤도면(orbital plane) 상에 존재한다.

$\overrightarrow{B}$ 는 B-벡터 또는 충격벡터(impact vector)로서 목표 행성의 중심으로부터 진입 점근선까지의 최단거리 벡터이며 진입 점근선과 직교한다. 따라서 $\hat{S}$ 와 직각인 $\overrightarrow{B}$ 는 궤도면과 B-평면에 동시에 존재한다.

B-벡터의 끝점, 쯕 B-벡터와 진입 점근선이 만나는 점을 조준점(aim point)라고 한다. 이 점은 도착지 행성의 중력이 우주비행체의 궤적에 영향을 미치지 않는 경우 우주비행체가 B-평면을 관통하는 지점을 가리킨다.

 

 

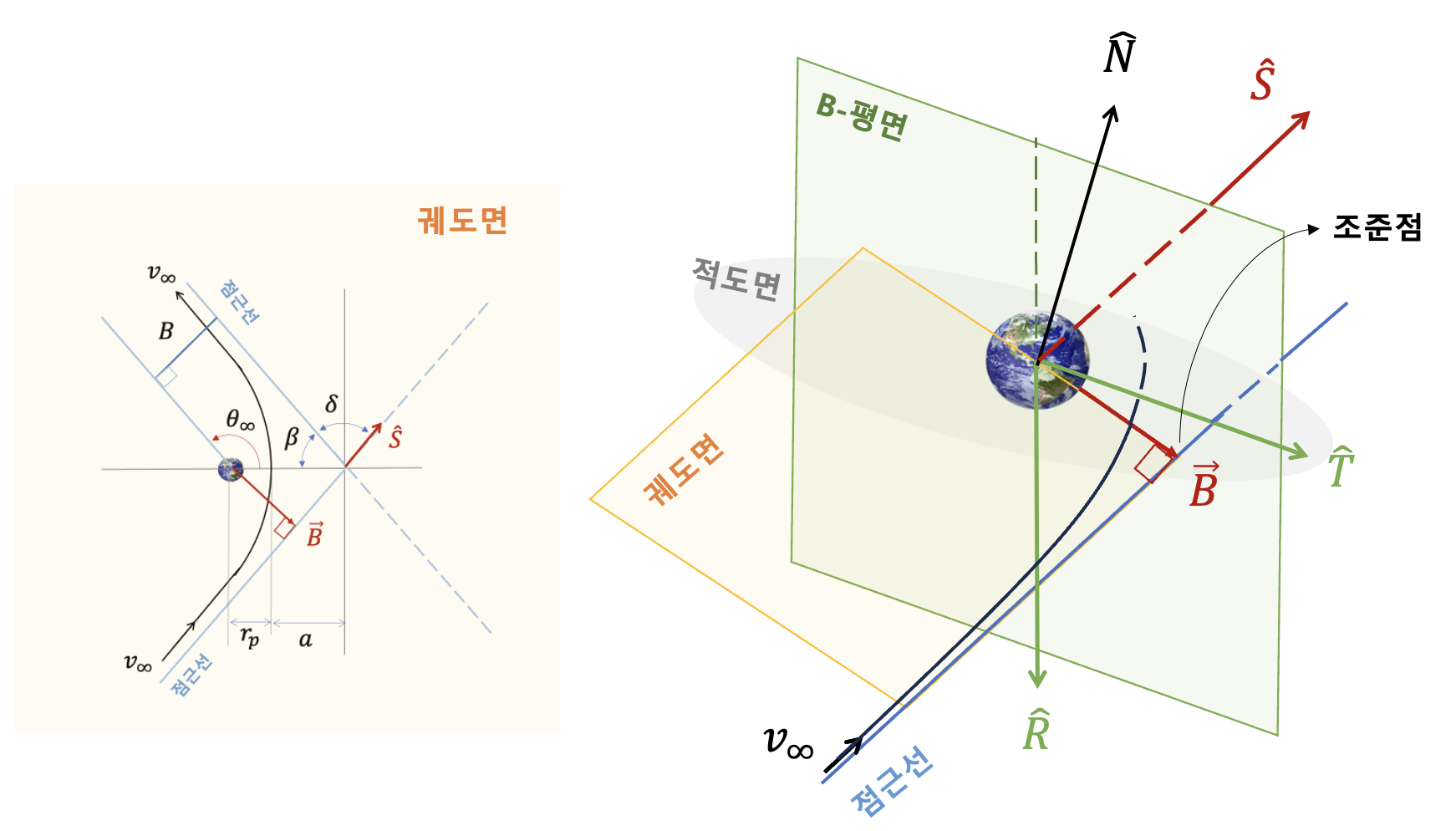
B-벡터를 표현하기 위해서 B-평면 상에 두개의 좌표축인 단위벡터 $\hat{T}$ 와 $\hat{R}$ 을 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(1)}& \hat{T}=\frac{\hat{S}\times \hat{N}}{|\hat{S}\times \hat{N}|},\hat{R}=\hat{S}\times \hat{T}\end{array}$$

 

여기서 $\hat{N}$ 은 $\hat{S}$ 와 평행하지 않은 단위벡터는 모두 가능하나 일반적으로 행성중심관성좌표계의 $z$축과 일치하도록 목표 행성의 적도면과 수직인 벡터로 정한다.

 

 

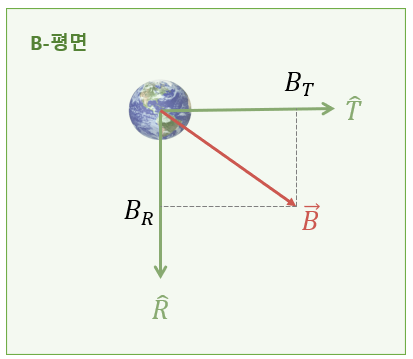
B-벡터를 $\hat{T}$ 축과 $\hat{R}$ 축으로 표현하면 다음과 같다.

 

$$\begin{array}{r}\text{(2)}& \overrightarrow{B}& =B_T\hat{T}+B_R\hat{R}\\ & =(\overrightarrow{B}\cdot \hat{T})\hat{T}+(\overrightarrow{B}\cdot \hat{R})\hat{R}\end{array}$$

 

쌍곡선 궤도의 기하학에 관한 게시글(https://pasus.tistory.com/359)의하면 B-벡터의 크기, 즉 충격파라미터(impact parameter)는 $B=\frac{h}{v_{\mathrm{\infty }}}$ 이므로 B-벡터는 다음과 같은 관계식을 갖는다.

 

$$\begin{array}{}\text{(3)}& \overrightarrow{B}=\frac{\hat{S}\times \overrightarrow{h}}{v_{\mathrm{\infty }}}\end{array}$$

 

식 (3)을 식 (2)에 대입하면 다음과 같이 B-벡터의 $\hat{T}$ 와 $\hat{R}$ 축 성분을 계산할 수 있다.

 

$$\begin{array}{r}\text{(4)}& B_T& =\frac{1}{v_{\mathrm{\infty }}}(\hat{S}\times \overrightarrow{h})\cdot \hat{T}=\frac{1}{v_{\mathrm{\infty }}}(\hat{T}\times \hat{S})\cdot \overrightarrow{h}=-\frac{\hat{R}\cdot \overrightarrow{h}}{v_{\mathrm{\infty }}}\\ B_R& =\frac{1}{v_{\mathrm{\infty }}}(\hat{S}\times \overrightarrow{h})\cdot \hat{R}=\frac{1}{v_{\mathrm{\infty }}}(\hat{R}\times \hat{S})\cdot \overrightarrow{h}=\frac{\hat{T}\cdot \overrightarrow{h}}{v_{\mathrm{\infty }}}\end{array}$$

 

점근선벡터 $\hat{S}$ 는 아래 그림과 같은 기하학적인 관계식을 이용하여 궤도중심좌표계(perifocal frame)로 표현할 수 있다.

 

$$\begin{array}{}\text{(5)}& \hat{S}=\cos \beta {\hat{p}}_1+\sin \beta {\hat{p}}_2\end{array}$$

 

여기서 $\beta$ 는 점근선 각도로서 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(6)}& \beta ={\cos }^{-1}\left(\frac{1}{e}\right)\end{array}$$

 

따라서

 

$$\begin{array}{r}\text{(7)}& & \cos \beta =\frac{1}{e}\\ & \sin \beta =\sqrt{1-{\cos }^2\beta }=\sqrt{\frac{e^2-1}{e^2}}\end{array}$$

 

이 된다.

 

 

정의에 의하면 궤도중심좌표계의 ${\hat{p}}_1$ 축은 이심율 벡터 $\overrightarrow{e}$ 와 평행하고 ${\hat{p}}_3$ 축은 각운동량 벡터 $\overrightarrow{h}$ 와 평행하다. 이를 이용하면 ${\hat{p}}_1$ 축과 ${\hat{p}}_2$ 축을 이심율 벡터와 각운동량 벡터의 함수로 표현할 수 있다.

 

$$\begin{array}{r}\text{(8)}& {\hat{p}}_1& =\frac{\overrightarrow{e}}{e}\\ {\hat{p}}_2& ={\hat{p}}_3\times {\hat{p}}_1=\frac{\overrightarrow{h}\times \overrightarrow{e}}{he}\end{array}$$

 

식 (7)과 (8)을 식 (5)에 대입하면 점근선벡터를 다음과 같이 이심율 벡터와 각운동량 벡터만의 함수로 표현할 수 있다.

 

$$\begin{array}{}\text{(9)}& \hat{S}=\frac{\overrightarrow{e}}{e^2}+\frac{\sqrt{e^2-1}}{e^2}\frac{\overrightarrow{h}\times \overrightarrow{e}}{h}\end{array}$$

 

여기서 운동량 벡터와 이심율 벡터는 다음과 같이 우주비행체의 위치벡터와 속도벡터만으로 계산할 수 있으며 궤도의 어느 위치에서 계산하더라도 일정한 값을 갖는다 (https://pasus.tistory.com/287).

 

$$\begin{array}{r}\text{(10)}& \overrightarrow{h}& =\overrightarrow{r}\times \overrightarrow{v}\\ \overrightarrow{e}& =\frac{1}{\mu }(\overrightarrow{v}\times \overrightarrow{h}-\mu \frac{\overrightarrow{r}}{r})\\ \\ & =\frac{1}{\mu }((v^2-\frac{\mu }{r})\overrightarrow{r}-(\overrightarrow{r}\cdot \overrightarrow{v})\overrightarrow{v})\end{array}$$

 

식 (1)에 의하면 $\hat{N}$ 는 우주비행체의 위치나 속도에 관계없이 목표 행성의 관성좌표계로 정해지기 때문에 $\hat{T}$ 축과 $\hat{R}$ 축은 $\hat{S}$ 만의 함수가 된다. 또한 식 (3)에 의하면 B-벡터도 $\hat{S},\overrightarrow{h},v_{\mathrm{\infty }}$ 로 정해지고 식 (9)와 (10)에 의하면 $\hat{S},\overrightarrow{h}$ 도 우주비행체의 위치벡터와 속도벡터만으로 계산할 수 있으므로 B-벡터와 B-평면 모두 우주비행체의 위치벡터와 속도벡터 및 $v_{\mathrm{\infty }}$ 만의 함수로 나타낼 수 있다.

한편 쌍곡선 궤도의 기하학에 관한 게시글(https://pasus.tistory.com/359)의하면 근지점까지의 거리는 다음식으로부터 계산할 수 있다.

 

$$\begin{array}{}\text{(11)}& B=r_p\sqrt{1+\frac{2\mu }{v_{\mathrm{\infty }}^2{r}_p}}\end{array}$$

 

양변을 제곱하고 근의 공식을 이용하면 $r_p$ 는 다음과 같이 계산된다.

 

$$\begin{array}{}\text{(12)}& r_p=-\frac{\mu }{v_{\mathrm{\infty }}^2}+\sqrt{\frac{{\mu }^2}{v_{\mathrm{\infty }}^4}+B^2}\end{array}$$

 

또한 케플러 방정식에 의하면 쌍곡선 궤도의 근지점에서 임의의 위치까지의 비행시간은 다음 식으로 나타낼 수 있다 (https://pasus.tistory.com/309).

 

$$\begin{array}{r}\text{(13)}& t& =\frac{h^3}{{\mu }^2}\frac{e\sinh F-F}{(e^2-1{)}^{3/2}}\\ & =\sqrt{\frac{(-a{)}^3}{\mu }}(e\sinh F-F)\end{array}$$

 

여기서 $a$ 는 쌍곡선 궤도의 장반경으로 $a<0$ 이며 $F$ 는 쌍곡선궤도의 이심 비행각(hyperbolic eccentric anomaly)이다.

 

 

식 (13)은 근지점부터 측정하기 시작한 비행시간이다. B-평면 문제에서는 외부로부터 목표 행성에 접근하기 때문에 임의의 위치에서부터 근지점까지 도달하는데 걸리는 시간으로 다시 작성해야 한다. 이 시간을 최근접 도달 시간(TCA, time to closest approach)이라고 한다. 그러면 식 (13)에서 실제 비행각과 이에 해당하는 이심 비행각이 모두 음수에 해당하므로 식 (13)을 다음과 같이 변경한다.

 

$$\begin{array}{}\text{(14)}& t_{TCA}=\sqrt{\frac{(-a{)}^3}{\mu }}(F-e\sinh F)\end{array}$$

 

여기서 이심 비행각과 실제 비헹각은 다음과 같은 관계식을 갖는다.

 

$$\begin{array}{}\text{(15)}& \tanh \frac{F}{2}=\sqrt{\frac{e-1}{e+1}}\tan \frac{\theta }{2}\end{array}$$

 

 

결론적으로 목표 행성을 기준으로 우주비행체의 현재 위치와 속도벡터 $\overrightarrow{r}$ 와 $\overrightarrow{v}$가 주어지면 지금까지 유도한 여러 방정식을 통해 B-평면과 조준점의 위치, 또는 B-벡터, 최근접 도달 시간 등을 계산할 수 있다.