[Continuous-Time] 관측가능성 (Observability)

다음과 같은 선형 시불변(LTI) 시스템이 있다.

 

$$\begin{array}{r}\text{(1)}& \dot{\mathbf{x}}& =A\mathbf{x}+B\mathbf{u}\\ \mathbf{y}& =C\mathbf{x}+D\mathbf{u}\end{array}$$

 

여기서 $\mathbf{x}(t)\in {\mathbb{R}}^n$ 는 상태변수, $\mathbf{u}(t)\in {\mathbb{R}}^p$ 는 제어입력, $\mathbf{y}(t)\in {\mathbb{R}}^q$ 는 제어입력이다.

만약 미지의 초기 상태 $\mathbf{x}(0)$ 에 대해 시간 범위 $t\in [0,t_1]$ 에서의 입력 $\mathbf{u}(t)$ 와 출력 $\mathbf{y}(t)$ 에 대한 정보를 바탕으로 초기 상태 $\mathbf{x}(0)$ 를 유일하게 결정하는데 충분한 유한 시간 $t_1>0$ 이 존재하는 경우 시스템 (1) 또는 행렬 $(C,A)$ 는 관측가능(observable)하다고 정의한다.

 

 

LTI 시스템에서 상태변수는 제어입력에 영향을 받으며 차례로 출력에 영향을 미친다. 보통 상태 방정식으로 모델링된 시스템의 상태변수 차원이 제어입력 또는 출력의 차원보다 크다 ($n>p,n>q)$. 이는 각 상태변수를 직접 작동시키거나 추정할 수 없다는 사실을 의미한다. 그럼에도 불구하고 상태변수를 추정해야할 필요가 있다.

관측가능성은 입력과 출력에 대한 지식으로 시스템의 내부 상태를 얼마나 잘 추정할 수 있는지를 측정하는 척도다. 왜냐하면 만약 입력 $\mathbf{u}(t)$ 와 출력 $\mathbf{y}(t)$ 를 이용하여 초기 상태 $\mathbf{x}(0)$ 를 유일하게 결정할 수 있다면 방정식 (1)로 주어지는 시스템의 전체 상태 궤적 $\mathbf{x}(t)$를 계산할 수 있기 때문이다.

그렇다면 시스템이 이러한 관측 ‘능력’을 보유하고 있는지 아닌지 어떻게 판단할 수 있을까.

방정식 (1)의 해는 다음과 같다.

 

$$\begin{array}{}\text{(2)}& \mathbf{y}(t)=C{e}^{At}\mathbf{x}(0)+C{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau +D\mathbf{u}(t)\end{array}$$

 

여기서 입력 $\mathbf{u}(t)$ 와 출력 $\mathbf{y}(t)$ 를 알고 있다고 가정하면 초기 상태 $\mathbf{x}(0)$ 만이 미지수이므로 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(3)}& \tilde{\mathbf{y}}(t)=C{e}^{At}\mathbf{x}(0)\end{array}$$

여기서

$$\begin{array}{r}\tilde{\mathbf{y}}(t)=\mathbf{y}(t)-C{\int }_0^t{e}^{A(t-\tau )}B\mathbf{u}(\tau )d\tau -D\mathbf{u}(t)\end{array}$$

 

는 알고 있는 값이다. 식 (3)에 의하면 결국 $\mathbf{u}(t)\equiv 0$ 로 가정해도 관측가능성에 대한 해석적 결과는 동일하다.

 

$$\begin{array}{r}\text{(4)}& \dot{\mathbf{x}}& =A\mathbf{x}\\ \mathbf{y}& =C\mathbf{x}\end{array}$$

 

따라서 여기서는 시스템 (4)를 이용하여 관측가능성에 대해 논의하고자 한다.

관측가능성에 관련하여 다음 3가지 명제는 동치이다.

(a) $(C,A)$는 관측가능하다.

(b) 어떤 $t_1>0$ 에 대해서도 $W_o(t_1)>0$ 이다. 여기서 $W_o$ 를 관측가능성 그래미안(observability gramian)이라고 하며 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(5)}& W_o(t_1)={\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{At}dt\end{array}$$

 

(c) $Q_o$ 의 랭크(rank)는 $n$ 이다. 여기서 $Q_o$ 를 관측가능성 행렬(observability matrix)이라고 하며 다음과 같이 정의한다.

 

$$\begin{array}{}\text{(6)}& Q_o=\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{n-1}\end{array}\right]\end{array}$$

 

증명은 다음과 같다.

 

 

1. (c) $\to$ (b)
‘(c) 이면 (b)다’라는 것을 직접 증명하기는 어려우므로 이와 동치인 ‘(b)가 아니면 (c)도 아니다’라는 명제를 대신 증명하겠다.
$W_o(t_1)$ 가 정정행렬(positive-definite matrix)이 아니라면 ${\mathbf{v}}^T{W}_o(t_1)\mathbf{v}=0$ 을 만족하는 어떤 벡터 $\mathbf{v}\ne 0$ 가 존재한다. 따라서

 

$$\begin{array}{r}\text{(7)}& 0& ={\mathbf{v}}^T{W}_o(t_1)\mathbf{v}={\mathbf{v}}^T\left({\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{At}dt\right)\mathbf{v}\\ & ={\int }_0^{t_1}{\mathbf{v}}^T{e}^{A^{T}t}{C}^{T}C{e}^{At}\mathbf{v}dt\\ \\ & ={\int }_0^{t_1}{\left(C{e}^{At}\mathbf{v}\right)}^T\left(C{e}^{At}\mathbf{v}\right)dt\\ \\ & ={\int }_0^{t_1}\Vert C{e}^{At}\mathbf{v}{\Vert }^{2}dt\end{array}$$

 

이므로 모든 $0\le t\le t_1$ 에 대해서 $C{e}^{At}\mathbf{v}\equiv 0$ 이 된다. 이는 곧 모든 시간 미분도 모든 시간 $t$ 에서 항상 $0$ 이 되어야 한다는 뜻이므로,

 

$$\begin{array}{rl}& C{e}^{At}\mathbf{v}=0\to C\mathbf{v}=0\\ \\ & CA{e}^{At}\mathbf{v}=0\to CA\mathbf{v}=0\\ \\ & C{A}^2{e}^{At}\mathbf{v}=0\to C{A}^2\mathbf{v}=0\\ \\ & ⋮\\ \\ & C{A}^{n-1}{e}^{At}\mathbf{v}=0\to C{A}^{n-1}\mathbf{v}=0\end{array}$$

 

가 된다. 따라서

 

$$\begin{array}{r}\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{n-1}\end{array}\right]\mathbf{v}=0=Q_o\mathbf{v}\end{array}$$

 

이므로 $rank(Q_o)<n$ 이 되어서 ‘(b)가 아니면 (c)도 아니다’ 라는 명제가 증명되었다.

2. (b) $\to$ (c)
이번에도 ‘(b) 이면 (c)다’라는 것을 직접 증명하기는 어려우므로 이와 동치인 ‘(c)가 아니면 (b)도 아니다’라는 명제를 대신 증명하겠다.
만약 $Q_o$ 의 랭크(rank)가 $n$ 이 아니라면 $Q_o\mathbf{v}=0$ 을 만족하는 어떤 벡터 $\mathbf{v}\ne 0$ 가 존재한다. 따라서

 

$$\begin{array}{r}\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{n-1}\end{array}\right]\mathbf{v}=0\end{array}$$

 

이다. 케일리-해밀톤 정리(https://pasus.tistory.com/335)에 의하면

 

$$\begin{array}{r}{e}^{At}=\sum _{i=0}^{n-1}{\beta }_i(t)A^i\end{array}$$

 

로 쓸 수 있으므로 다음 식이 성립한다.

 

$$\begin{array}{r}C{e}^{At}\mathbf{v}=\sum _{i=0}^{n-1}{\beta }_i(t)C{A}^i\mathbf{v}=0\end{array}$$

 

따라서

 

$$\begin{array}{rl}{W}_o(t_1)\mathbf{v}& =\left({\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{At}dt\right)\mathbf{v}\\ \\ & ={\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{At}\mathbf{v}dt=0\end{array}$$

 

이 되므로 $W_o(t_1)$ 는 정정행렬이 아니다.

3. (b) $\to$ (a)
어떤 $t_1>0$ 에서 식 (4)의 해는 다음과 같다.

 

$$\begin{array}{}\text{(8)}& \mathbf{y}(t)=e^{At}\mathbf{x}(0)\end{array}$$

 

이제 다음 관계식을 보자.

 

$$\begin{array}{rl}{\int }_0^{t_1}{e}^{A^{T}t}{C}^T\mathbf{y}(t)dt& ={\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{A{t}_1}\mathbf{x}(0)dt\\ \\ & =\left({\int }_0^{t_1}{e}^{A^{T}t}{C}^{T}C{e}^{At}dt\right)\mathbf{x}(0)\\ \\ & =W_o(t_1)\mathbf{x}(0)\end{array}$$

 

위 식에 의하면

 

$$\begin{array}{r}\mathbf{x}(0)=W_o^{-1}(t_1){\int }_0^{t_1}{e}^{A^{T}t}{C}^T\mathbf{y}(t)dt\end{array}$$

 

이 되므로 $W_o(t_1)>0$ 이면 시스템의 초기상태 $\mathbf{x}(0)$ 를 계산할 수 있다.

4. (a) $\to$ (b)
이번에도 '(a) 이면 (b)다'라는 것을 직접 증명하기는 어려우므로 이와 동치인 '(b)가 아니면 (a)도 아니다'라는 명제를 대신 증명하겠다.
$W_o(t_1)>0$ 이 아니라면 ${\mathbf{v}}^T{W}_o(t_1)\mathbf{v}=0$ 을 만족하는 어떤 벡터 $\mathbf{v}\ne 0$ 가 존재한다. 따라서 식 (7)에 의하면 모든 $0\le t\le t_1$ 에 대해서 $C{e}^{At}\mathbf{v}\equiv 0$ 이 된다. 그런데 만약 $\mathbf{y}(t)=C{e}^{At}{\mathbf{x}}_1(0)$ 이라면

 

$$\begin{array}{rl}\mathbf{y}(t)& =C{e}^{At}({\mathbf{x}}_1(0)+\mathbf{v})\\ \\ & =C{e}^{At}{\mathbf{x}}_2(0)\end{array}$$

 

로 이 되므로 동일한 $\mathbf{y}(t)$ 에 대한 초기 상태가 유일하지 않기 때문에 시스템은 관측가능하지 않다.

(a) $\to$ (c) 의 증명은 (a) $\to$ (b) $\to$ (c)의 순서로, (c) $\to$(a) 의 증명은 (c)$\to$ (b) $\to$ (a)의 순서로 증명하면 된다.

 

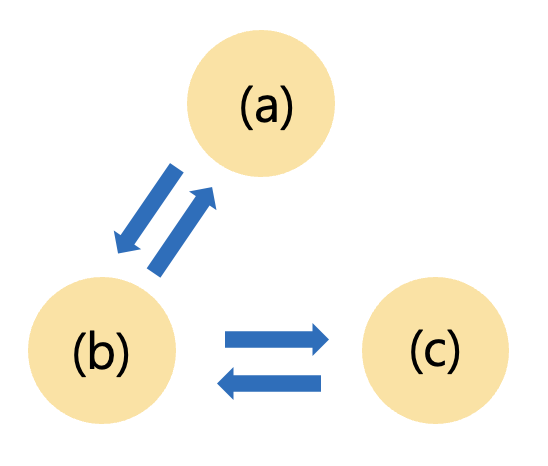
로 따라서 증명 1,2,3,4에 의해서 관측가능성에 관련한 3가지 명제가 동치임을 증명하였다. 보통 어떤 시스템이 관측가능한지의 여부는 식 (6)의 관측가능성 행렬의 랭크를 계산해서 확인한다.