질량중심을 기준으로 한 강체의 운동방정식은 다음과 같았다 (https://pasus.tistory.com/191).
\[ \begin{align} \vec{M}_G &= \frac{ ^bd \vec{H}_G}{dt}+ \ ^i\vec{\omega} ^b \times \vec{H}_G \tag{1} \\ \\ &= \bar{I}_G \cdot \frac{ ^b d \ ^i\vec{\omega} ^b }{dt} + \ ^i\vec{\omega} ^b \times (\bar{I}_G \cdot \ ^i\vec{\omega} ^b ) \end{align} \]
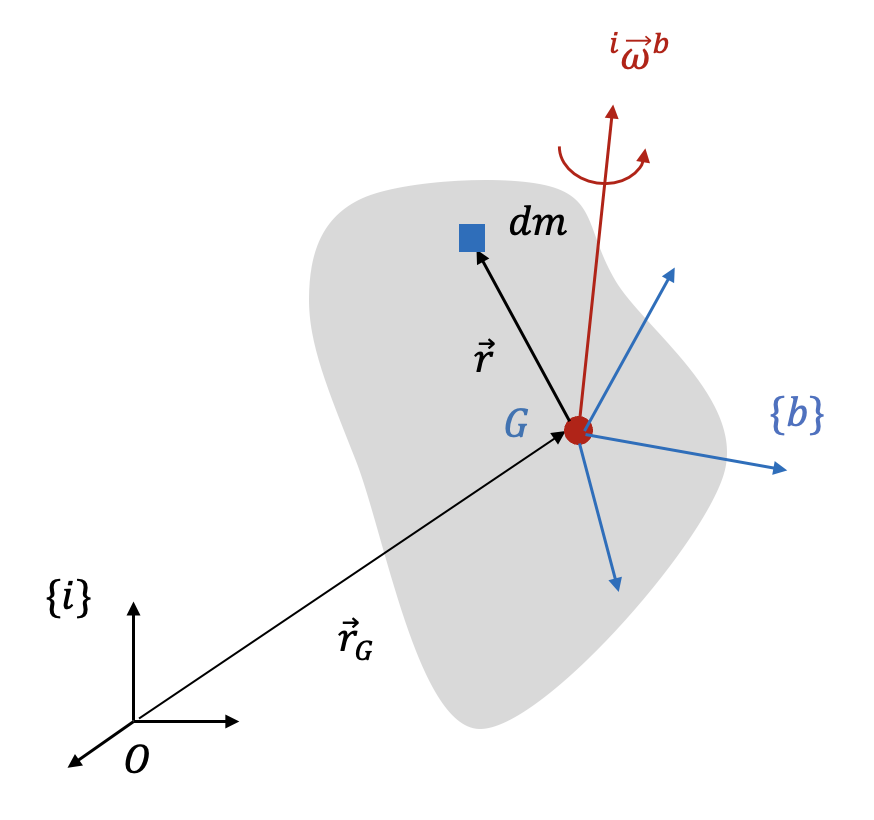
여기서 \( ^i \vec{\omega} ^b\) 는 관성 좌표계 \(\{i\}\) 에 대한 강체 좌표계 \(\{b\}\) 의 각속도벡터, \(\bar{I}_G\) 는 강체의 질량중심점 \(G\) 에 관한 관성 다이아딕(inertia dyadic), \(\vec{M}_G\) 와 \(\vec{H}_G\) 는 각각 질량중심점에 관한 모멘트와 각운동량 벡터다.
이제 식 (1)의 각 항을 각각 다음과 같이 강체 좌표계 \(\{b\}\) 로 표현해 보자.
\[ \begin{align} & \vec{M}_G = M_x \hat{b}_1+M_y \hat{b}_2+M_z \hat{b}_3 \tag{2} \\ \\ & \vec{H}_G = H_x \hat{b}_1+H_y \hat{b}_2+H_z \hat{b}_3 \\ \\ & ^i \vec{\omega}^b = \omega_x \hat{b}_1+ \omega_y \hat{b}_2+ \omega_z \hat{b}_3 \\ \\ & \bar{I}_G = \sum_{i=1}^3 \sum_{j=1}^3 I_{ij} \hat{b}_i \hat{b}_j \\ \\ & \vec{r} = x \hat{b}_1+y \hat{b}_2+z \hat{b}_3 \end{align} \]
식 (2)를 이용하여 각운동량 벡터를 좌표계 \(\{b\}\) 로 표현하면 다음과 같다.
\[ \begin{align} & H_G^b=[I_G^b] \omega_{ib}^b \tag{3} \\ \\ \to \ & \begin{bmatrix} H_x \\ H_y \\ H_z \end{bmatrix}= \begin{bmatrix}I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yz} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{bmatrix} \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \end{align} \]
여기서 관성모멘트(MOI, moment of inertia) \(I_{xx}, \ I_{yy}, \ I_{zz}\) 와 관성곱(product of inertia) \(I_{xy}, \ I_{xz}, \ I_{yx}, \ I_{yz}, \ I_{zx}, \ I_{zy}\) 는 다음과 같다.
\[ \begin{align} & I_{xx}= \int (y^2+z^2 ) \ dm, \ \ \ \ \ I_{xy}=I_{yx}= \int xy \ dm \tag{4} \\ \\ & I_{xz}=I_{zx}= \int xz \ dm, \ \ \ \ \ I_{yy}= \int (x^2+z^2 ) \ dm \\ \\ & I_{yz}=I_{zy}= \int yz \ dm, \ \ \ \ \ I_{zz}= \int (x^2+y^2) \ dm \end{align} \]
식 (3)에서 관성곱에 있는 음(\(-\))의 부호는 관성곱을 식 (4)와 같이 정의하기 때문에 붙은 것이다.
이제 식 (2)와 (3)을 이용하여 식 (1)의 회전 운동방정식을 좌표계 \(\{b\}\) 로 표현하면 다음과 같다.
\[ \begin{align} & M_G^b = \dot{H}_G^b+[\omega_{ib}^b \times] H_G^b \tag{5} \\ \\ \to \ & \begin{bmatrix} M_x \\ M_y \\ M_z \end{bmatrix} = \begin{bmatrix} \dot{H}_x \\ \dot{H}_y \\ \dot{H}_z \end{bmatrix} + \begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix} \begin{bmatrix} H_x \\ H_y \\ H_z \end{bmatrix} \\ \\ & \ \ \ \ \ \ \ \ \ \ \ = \begin{bmatrix} \dot{H}_x- H_y \omega_z+H_z \omega_y \\ \dot{H}_y+H_x \omega_z-H_z \omega_x \\ \dot{H}_z-H_x \omega_y+H_y \omega_x \end{bmatrix} \end{align} \]
식 (5)를 풀어 쓰면 다음과 같다.
\[ \begin{align} M_x &= I_{xx} \dot{\omega}_x-I_{xy} \dot{\omega}_y-I_{xz} \dot{\omega}_z-(-I_{yx} \omega_x+I_{yy} \omega_y-I_{yz} \omega_z ) \omega_z \tag{6} \\ \\ & \ \ \ \ \ +(-I_{zx} \omega_x-I_{zy} \omega_y+I_{zz} \omega_z ) \omega_y \\ \\ M_y &= -I_{yx} \dot{\omega}_x+I_{yy} \dot{\omega}_y-I_{yz} \dot{\omega}_z+(I_{xx} \omega_x-I_{xy} \omega_y-I_{xz} \omega_z ) \omega_z \\ \\ & \ \ \ \ \ -(-I_{zx} \omega_x-I_{zy} \omega_y+I_{zz} \omega_z ) \omega_x \\ \\ M_z & = -I_{zx} \dot{\omega}_x-I_{zy} \dot{\omega}_y+I_{zz} \dot{\omega}_z-(I_{xx} \omega_x-I_{xy} \omega_y-I_{xz} \omega_z ) \omega_y \\ \\ & \ \ \ \ \ +(-I_{yx} \omega_x+I_{yy} \omega_y-I_{yz} \omega_z ) \omega_x \end{align} \]

만약 일반적인 항공기의 형상과 같이 강체가 xz 평면에 대해서 대칭(symmetry)이라면 관성곱 \(I_{xy}=I_{yz}=0\) 이므로 (https://pasus.tistory.com/244) 식 (6)은 다음과 같이 간략화 된다.
\[ \begin{align} & M_x= I_{xx} \dot{\omega}_x-I_{xz} \dot{\omega}_z-I_{zx} \omega_x \omega_y+(I_{zz}-I_{yy} ) \omega_y \omega_z \tag{7} \\ \\ & M_y= I_{yy} \dot{\omega}_y+(I_{xx}-I_{zz} ) \omega_x \omega_z+I_{xz} (\omega_x^2-\omega_z^2 ) \\ \\ & M_z= -I_{xz} \dot{\omega}_x+I_{zz} \dot{\omega}_z+(I_{yy}-I_{xx} ) \omega_x \omega_y+I_{xz} \omega_y \omega_z \end{align} \]
이 때 식 (3)의 각운동량은 다음과 같이 간략화 된다.
\[ \begin{align} & H_x= I_{xx} \omega_x-I_{xz} \omega_z \tag{8} \\ \\ & H_y= I_{yy} \omega_y \\ \\ & H_z= I_{zz} \omega_z-I_{xz} \omega_x \end{align} \]
만약 강체 좌표계의 각 축의 방향이 관성 주축(principal axes of inertia)과 일치한다면 관성곱은 모두 \(0\) 이 되므로 식 (7)은 다음과 같이 더욱 간단해 진다.
\[ \begin{align} & M_x= I_{xx} \dot{\omega}_x+(I_{zz}-I_{yy} ) \omega_y \omega_z \tag{9} \\ \\ & M_y= I_{yy} \dot{\omega}_y+(I_{xx}-I_{zz} ) \omega_x \omega_z \\ \\ & M_z= I_{zz} \dot{\omega}_z+(I_{yy}-I_{xx} ) \omega_x \omega_y \end{align} \]
식 (9)를 오일러의 운동방정식(Euler’s equation of motion)이라고 한다. 이 때 식 (8)의 각운동량은 다음과 같다.
\[ \begin{align} & H_x= I_{xx} \omega_x \tag{10} \\ \\ & H_y= I_{yy} \omega_y \\ \\ & H_z= I_{zz} \omega_z \end{align} \]
'항공우주 > 동역학' 카테고리의 다른 글
| 로드리게스 파라미터 (0) | 2025.06.01 |
|---|---|
| 회전벡터 (Rotation Vector)의 시간 변화율 (0) | 2025.04.09 |
| 관성 주축 (Principal Axes of Inertia) (0) | 2023.02.19 |
| 좌표변환과 관성행렬 (Inertia Matrix) (0) | 2023.02.17 |
| 오일러의 회전 정리 (Euler’s Rotation Theorem) (0) | 2022.03.22 |




댓글