중력 영향권 (Sphere of Influence)

우주비행체가 지구에서 출발하여 태양계 내의 다른 행성으로 비행한다고 하자. 이 우주비헹체는 지구의 영향권에서 벗어나면 태양의 영향권으로 들어가고, 태양의 영향권에서 벗어나면 도착 행성의 영향권으로 들어갈 것이다. 지구의 영향권 내에서는 지구에 인한 중력이 우주비행체에 작용하는 주된 힘(force)이고, 태양을 비롯한 다른 천체로 인한 중력은 교란(disturbance)으로 간주할 수 있다. 따라서 지구의 영향권 내에서는 우주비행체의 운동방정식을 지구중심 관성좌표계(ECI)로 작성하는 것이 유리할 것이다 (https://pasus.tistory.com/184).

마찬가지로 태양의 영향권 내에서는 태양의 중력이 우주비행체에 작용하는 주된 힘이고 지구를 비롯한 다른 천체로 인한 중력은 교란으로 간주할 수 있다. 따라서 태양의 영향권 내에서는 태양중심 관성좌표계(SCI)에서 우주비행체의 운동 방정식을 만드는 것이 유리할 것이다.

문제는 지구로부터 우주비행체까지 주어진 거리에 대해서 어느 좌표계를 선택하느냐에 관한 것이다. 또는 지구로부터 어느 정도 거리까지 지구의 중력 영향권으로 간주할 것이냐 하는 것이다.

 

 

라플라스(Laplace)는 주된 힘에 대한 교란력의 비가 더 작은 영역을 기준으로 좌표계를 선택할 것을 제안했다. 이 영역을 '중력 영향권 (SOI, sphere of influence)'이라고 한다.

아래 그림과 같이 질량이 \(m_1\) 과 \(m_2\), \(m\) 인 세 질점이 각각 일정 거리만큼 서로 떨어져 있고, 세 질점 간에는 오직 만유인력만 작용한다고 가정하자.

 

 

그림에서 \(\{i\}\) 는 관성좌표계, \(\vec{r}_1\) 은 관성좌표계의 원점에서 질점 \(m_1\) 까지의 위치벡터, \(\vec{r}_2\) 는 질점 \(m_2\) 까지의 위치벡터, \(\vec{r}_3\) 는 질점 \(m\) 까지의 위치벡터이며, \(\vec{r}_{21}\) 는 질점 \(m_2\) 에서 \(m_1\) 까지의 위치벡터, \(\vec{d}\) 는 질점 \(m_1\) 에서 \(m\) 까지의 위치벡터, \(\vec{r}\) 은 질점 \(m_2\) 에서 \(m\) 까지의 위치벡터이다. \(\gamma\) 는 위치벡터 \(\vec{r}\) 과 \(\vec{r}_{21}\) 의 사잇각이다.

세 질점 중 한 개의 질점의 질량 m의 질량은 다른 두 질점 보다 훨씬 작아서 무시할 수 있을 정도라고 가정하자. 즉, \(m_1≫m\), \(m_2≫m\). 그러면 질점 \(m\) 은 두 질점 \(m_1\) 및 \(m_2\) 의 운동에는 어떤 영향도 미치지 못할 것이다.

만유인력의 법칙에 의하면 질점 \(m_1\) 에는 질점 \(m_2\) 방향과 질점 \(m\) 방향으로 힘이 작용하므로 질점 \(m_1\) 의 운동방정식은 뉴턴의 제2법칙에 의해서 다음과 같이 주어진다.

 

\[ G \frac{m_1 m}{d^2} \frac{\vec{d}}{d}-G \frac{m_1 m_2}{r_{21}^2 } \frac{\vec{r}_{21}}{r_{21}} = m_1 \frac{ ^i d^2 \vec{r}_1 }{dt^2 } \tag{1} \]

 

여기서 \(G\) 는 만유인력 상수, \(d\) 와 \(r_{21}\) 은 각각 위치벡터 \(\vec{d}\) 와 \(\vec{r}_{21}\) 의 크기다. 수식에 있는 음(\(-\))의 부호는 질점에 작용하는 힘이 위치벡터와 반대방향으로 작용한다는 것을 의미한다.

한편 질점 \(m_2\) 와 \(m\) 에도 만유인력이 작용하므로 질점 \(m_2\) 와 \(m\) 의 운동방정식은 각각 다음과 같이 구할 수 있다.

 

\[ \begin{align} & G \frac{m_1 m_2}{ r_21^2 } \frac{\vec{r}_{21}}{r_{21}} + G \frac{m_2 m}{r^2} \frac{\vec{r}}{r} = m_2 \frac{ ^i d^2 \vec{r}_2 }{dt^2 } \tag{2} \\ \\ - & G \frac{ m_1 m}{d^2} \frac{\vec{d}}{d}-G \frac{m_2 m}{r^2} \frac{\vec{r}}{r} = m \frac{ ^i d^2 \vec{r}_3 }{dt^2} \tag{3} \end{align} \]

 

이제, 질점 \(m_1\) 에 대한 질점 \(m\) 의 상대 운동을 기술하기 위해 식 (3)에서 (1)을 빼 본다.

 

\[ \begin{align} -G \frac{m_1}{d^2} \frac{\vec{d}}{d}-G \frac{m_2}{r^2} \frac{\vec{r}}{r}-G \frac{m}{d^2} \frac{\vec{d}}{d}+G \frac{m_2}{r_{21}^2} \frac{\vec{r}_{21}}{r_{21}} = \frac{ ^id^2 \vec{r}_3 }{dt^2 }- \frac{ ^i d^2 \vec{r}_1 }{dt^2} \tag{4} \end{align} \]

 

여기서 \( \vec{d}= \vec{r}_3-\vec{r}_1\) 임을 이용하면, 위 식은 다음과 같이 된다.

 

\[ \begin{align} \frac{ ^i d^2 \vec{d} }{dt^2 }+ G \frac{(m_1+m)}{d^2} \frac{\vec{d}}{d} &=-G \frac{m_2}{r^2} \frac{\vec{r}}{r}+G \frac{m_2}{ r_{21}^2 } \frac{ \vec{r}_{21}}{r_{21}} \tag{5} \\ \\ &=-G m_2 \left( \frac{\vec{r}}{r^3} - \frac{ \vec{r}_{21} }{ r_{21}^3 } \right) \end{align} \]

 

또한 질점 \(m_2\) 에 대한 질점 \(m\) 의 상대 운동을 기술하기 위해 식 (3)에서 (2)를 빼 본다.

 

\[ \begin{align} -G \frac{m_1}{d^2} \frac{\vec{d}}{d}-G \frac{m_2}{r^2} \frac{\vec{r}}{r}-G \frac{m_1}{r_{21}^2} \frac{\vec{r}_{21}}{r_{21}} -G \frac{m}{r^2} \frac{\vec{r}}{r} = \frac{ ^i d^2 \vec{r}_3 }{dt^2 }- \frac{ ^i d^2 \vec{r}_2 }{dt^2 } \tag{6} \end{align} \]

 

여기서 \(\vec{r}= \vec{r}_3- \vec{r}_2\) 임을 이용하면, 위 식은 다음과 같이 된다.

 

\[ \begin{align} \frac{ ^i d^2 \vec{r} }{dt^2 }+ G \frac{(m_2+m)}{r^2} \frac{\vec{r}}{r} &=-G \frac{m_1}{d^2} \frac{\vec{d}}{d}-G \frac{m_1}{r_{21}^2 } \frac{\vec{r}_{21}}{r_{21}} \tag{7} \\ \\ &=-G m_1 \left( \frac{\vec{d}}{d^3 } + \frac{ \vec{r}_{21}}{r_{21}^3 } \right) \end{align} \]

 

식 (5)는 질점 \(m\) 의 질점 \(m_1\) 에 대한 상대 운동방정식이고 식 (7)은 질점 \(m\) 의 질점 \(m_2\) 에 대한 상대 운동방정식이다. 두 식과 이체문제 (two-body problem)의 운동방정식과의 차이점은 식 (5)와 (7)에는 각각 질점 \(m_2\) 와 질점 \(m_1\) 에 의한 교란 항이 있다는 점이다.

식 (5)와 (7)에서 주된 힘에 의한 가속도와 교란력에 의한 가속도 항을 각각 써보자.

 

\[ \begin{align} & \vec{a}_1=-G \frac{ (m_1+m)}{d^2} \frac{\vec{d}}{d} \tag{8} \\ \\ & \vec{a}_{1d}= -Gm_2 \left( \frac{\vec{r}}{r^3} - \frac{\vec{r}_{21}}{r_{21}^3} \right) = \frac{Gm_2}{r^2} \left( \left( \frac{r}{r_{21} } \right)^2 \hat{e}_{21}- \hat{e}_r \right) \\ \\ & \vec{a}_2=-G \frac{(m_2+m)}{r^2} \frac{\vec{r}}{r} \tag{9} \\ \\ & \vec{a}_{d2}=-Gm_1 \left( \frac{\vec{d}}{d^3} + \frac{\vec{r}_{21}}{r_{21}^3 } \right) \end{align} \]

 

여기서 \(\vec{a}_1\) 과 \(\vec{a}_2\) 는 주된 힘에 의한 가속도, \(\vec{a}_{1d}\) 와 \(\vec{a}_{d2}\) 는 교란력에 의한 가속도, \(\hat{e}_{21}= \frac{\vec{r}_{21}}{r_{21}}\), \(\hat{e}_r= \frac{\vec{r}}{r}\) 이다.

 

 

이제부터 주된 가속도와 교란 가속도의 크기 비를 구하려고 한다. 조금 복잡한 식의 전개가 필요한데 우선 몇가지 유용한 관계식부터 유도한다.

 

 

먼저 \(\vec{d}= \vec{r}- \vec{r}_{21}\) 이고 \(d^2= \vec{d} \cdot \vec{d}\) 이므로 다음 관계식이 성립한다.

 

\[ \begin{align} \frac{d^2}{r_{21}^2} &= \frac{ (\vec{r}- \vec{r}_{21} ) \cdot (\vec{r}-\vec{r}_{21} )}{r_{21}^2 } \tag{10} \\ \\ &= \frac{1}{r_{21}^2 } (r^2-2r r_{21} \cos \gamma +r_{21}^2 ) \\ \\ &= 1-2 \frac{r}{r_{21}} \cos \gamma + \left( \frac{r}{r_{21}} \right)^2 \end{align} \]

 

또한 식 (9)의 교란 가속도 식의 오른쪽 항은 다음과 같이 쓸 수 있다.

 

\[ \begin{align} \frac{ \vec{d}}{d^3} + \frac{\vec{r}_{21} }{r_{21}^3 }= - \frac{ \partial }{ \partial \vec{r} } \left( \frac{1}{d}- \frac{1}{r_{21}^3 } \vec{r} \cdot \vec{r}_{21} \right) \tag{11} \end{align} \]

 

위 식의 성립여부는 식 오른쪽 항의 미분을 직접해보면 알 수 있다.

 

\[ \begin{align} & \frac{ \partial }{\partial \vec{r} } \left( \frac{1}{d} \right) =\frac{ \partial }{\partial \vec{r} } ((\vec{r}-\vec{r}_{21}) \cdot (\vec{r}-\vec{r}_{21}) )^{-1/2} \tag{12} \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = - ((\vec{r}-\vec{r}_{21}) \cdot (\vec{r}-\vec{r}_{21}) )^{-3/2} (\vec{r}-\vec{r}_{21}) \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = - \frac{\vec{d}}{d^3} \\ \\ & \frac{ \partial }{ \partial \vec{r} } \left( \frac{1}{r_{21}^3 } \vec{r} \cdot \vec{r}_{21} \right) = \frac{\vec{r}_{21}}{r_{21}^3 } \end{align} \]

 

식 (11)을 (9)에 대입하면 교란 가속도는 다음과 같이 된다.

 

\[ \begin{align} \vec{a}_{d2} &= Gm_1 \frac{ \partial }{ \partial \vec{r} } \left( \frac{1}{d}- \frac{1}{r_{21}^3} \vec{r} \cdot \vec{r}_{21} \right) \tag{13} \\ \\ &=\frac{ \partial }{ \partial \vec{r} } \left( \frac{G m_1}{r_{21}} \left( \frac{r_{21}}{d}- \frac{r}{r_{21}} \cos \gamma \right) \right) \end{align} \]

 

여기서

 

\[ \begin{align} R= \frac{G m_1}{r_{21}} \left( \frac{r_{21}}{d}- \frac{r}{r_{21}} \cos \gamma \right) \tag{14} \end{align} \]

 

로 놓으면, 식 (13)은 다음과 같이 된다.

 

\[ \begin{align} \vec{a}_{d2} = \frac{ \partial R}{ \partial \vec{r} } \tag{15} \end{align} \]

 

한편 식 (10)에 의하면,

 

\[ \begin{align} \frac{r_{21}}{d}= \left( 1-2 \frac{r}{r_{21}} \cos \gamma + \left( \frac{r}{r_{21}} \right)^2 \right)^{-\frac{1}{2}} \tag{16} \end{align} \]

 

이 되는데, 식 (16)은 르장드르 다항식(Legendre polynomials)으로 표현할 수 있다. 즉 르장드르 다항식은 생성함수(generating function)를 통해서 다음과 같이 정의할 수도 있는데

 

\[ \begin{align} (1-2 \nu x+x^2 )^{-\frac{1}{2}}= \sum_{k=0}^\infty x^k P_k (\nu), \ \ \ \vert x \vert \lt 1 \tag{17} \end{align} \]

 

식 (17)에서 \(x= \frac{r}{r_{21}}\) 로, \(\nu =\cos \gamma\) 로 놓으면 식 (16)과 일치하기 때문이다. 식 (17)은 왼쪽항을 이항정리(binomial theorem)를 이용하여 무한 급수로 전개하는 방법으로 증명할 수 있다. 식 (17)에서 \(P_k (\nu)\) 는 \(k\) 차 르장드르 다항식으로서 다음과 같이 주어진다 (https://pasus.tistory.com/175).

 

\[ \begin{align} & P_0 (\nu)=1 \tag{18} \\ \\ & P_1 (\nu)= \nu \\ \\ & P_2 (\nu )= \frac{1}{2} (3 \nu^2-1) \\ \\ & \ \ \ \ \ \cdots \end{align} \]

 

식 (16), (17), (18)을 식 (14)에 대입하면 다음과 같다.

 

\[ \begin{align} R &= \frac{Gm_1}{r_{21}} \left( \sum_{k=0}^\infty \left( \frac{r}{r_{21}} \right)^k P_k (\cos \gamma ) -\frac{r}{r_{21}} \cos \gamma \right) \tag{19} \\ \\ &= \frac{Gm_1 }{r_{21}} \left[ 1+ \sum_{k=2}^\infty \left( \frac{r}{r_{21}} \right)^k P_k (\cos \gamma) \right] \end{align} \]

 

또한 식 (19)를 (15)에 대입하면 교란 가속도 \(\vec{a}_{d2}\) 는 다음과 같이 된다.

 

\[ \begin{align} \vec{a}_{d2}= \frac{Gm_1}{r_{21}^2} \sum_{k=1}^\infty \left( \frac{r}{r_{21}} \right)^k \left[ P_{k+1}^\prime (\cos \gamma) \hat{e}_{21}-P_k^\prime (\cos \gamma ) \hat{e}_r \right] \end{align} \]

 

여기서 다음과 같은 미분 관계식,

 

\[ \begin{align} \frac{ \partial }{ \partial \vec{r} } P_k (\cos \gamma ) &= P_k^\prime (\cos \gamma ) \frac{ \partial }{ \partial \vec{r} } \cos \gamma \tag{21} \\ \\ &= P_k^\prime (\cos \gamma ) \frac{ \partial }{ \partial \vec{r} } \left( \frac{ \vec{r} \cdot \hat{e}_{21}}{r} \right) \\ \\ &= P_k^\prime (\cos \gamma ) \left[ \frac{ \hat{e}_{21} r- \vec{r} \cdot \hat{e}_{21} \hat{e}_r}{r^2} \right] \\ \\ &= \frac{1}{r} P_k^\prime (\cos \gamma ) \left[ \hat{e}_{21}- \cos \gamma \hat{e}_r \right] \end{align} \]

 

과 르장드르 다항식에 관련된 항등식,

 

\[ \begin{align} kP_k (\cos \gamma )=P_k^\prime (\cos \gamma ) \cos \gamma -P_{k-1}^\prime (\cos \gamma ) \tag{22} \end{align} \]

 

을 이용하였다.

 

 

이제 식 (8)로부터 질점 \(m_1\) 에 의한 주된 가속도와 질점 \(m_2\) 에 의한 교란 가속도의 크기 비를 구하면 다음과 같다.

 

\[ \begin{align} \frac{a_{1d}}{a_1} &= \left| \frac{\vec{a}_{1d}}{\vec{a}_1} \right| \tag{23} \\ \\ &= \frac{m_2}{m_1+m} \frac{d^2}{r^2} \left| \left( \frac{r}{r_{21}} \right)^2 \hat{e}_{21}- \hat{e}_r \right| \\ \\ & = \frac{m_2}{m_1+m} \frac{d^2}{r^2} \sqrt{ \left( \frac{r}{r_{21}} \right)^4+1-2 \left( \frac{r}{r_{21}} \right)^2 \cos \gamma } \end{align} \]

 

여기서 식 (10)을 이용하면,

 

\[ \begin{align} \frac{d^2}{r^2} &= \frac{d^2}{r_{21}^2 } \frac{r_{21}^2}{r^2} \tag{24} \\ \\ &= \frac{1}{ \left( \frac{r}{r_{21}} \right)^2} \left( 1-2 \frac{r}{r_{21}} \cos \gamma+ \left( \frac{r}{r_{21}} \right)^2 \right) \end{align} \]

 

이 되므로 식 (23)은 다음과 같이 된다.

 

\[ \begin{align} \frac{a_{1d}}{a_1} & = \frac{m_2}{m_1+m} \frac{1}{ \left( \frac{r}{r_{21}} \right)^2} \left( 1-2 \frac{r}{r_{21}} \cos \gamma+ \left( \frac{r}{r_{21}} \right)^2 \right) \\ & \ \ \ \ \ \ \ \ \ \ \times \sqrt{ \left( \frac{r}{r_{21}} \right)^4+1-2 \left( \frac{r}{r_{21}} \right)^2 \cos \gamma } \tag{25} \end{align} \]

 

또한 식 (9)와 (20)으로부터 질점 \(m_2\) 에 의한 주된 가속도와 질점 \(m_1\) 에 의한 교란 가속도의 크기 비를 구하면 다음과 같다.

 

\[ \begin{align} \frac{a_{2d}}{a_2} &= \left| \frac{ \vec{a}_{2d}}{\vec{a}_2} \right| \tag{26} \\ \\ &= \frac{m_1}{m_2+m} \left( \frac{r}{r_{21}} \right)^2 \left| \sum_{k=0}^\infty \left( \frac{r}{r_{21}} \right)^k \left[ P_{k+1}^\prime (\cos \gamma) \hat{e}_{21}-P_k^\prime (\cos \gamma ) \hat{e}_r \right] \right| \\ \\ &=\frac{m_1}{m_2+m} \left( \frac{r}{r_{21}} \right)^2 \left[ \left( \frac{r}{r_{21}} \right) \sqrt{ 9 \cos^2 \gamma+1-6 \cos^2 \gamma }+ \mathcal{O} \left( \left( \frac{r}{r_{21}} \right)^2 \right) \right] \\ \\ &= \frac{m_1}{m_2+m} \left( \frac{r}{r_{21}} \right)^3 \sqrt{1+3 \cos^2 \gamma }+ \mathcal{O} \left( \left( \frac{r}{r_{21}} \right)^4 \right) \end{align} \]

 

라플라스에 따르면, 식 (25)와 (26)에서 주된 가속도와 교란 가속도의 비가 작은 쪽이 질점 \(m\) 에 작용하는 중력이 더 우세하다고 볼 수 있다.

 

 

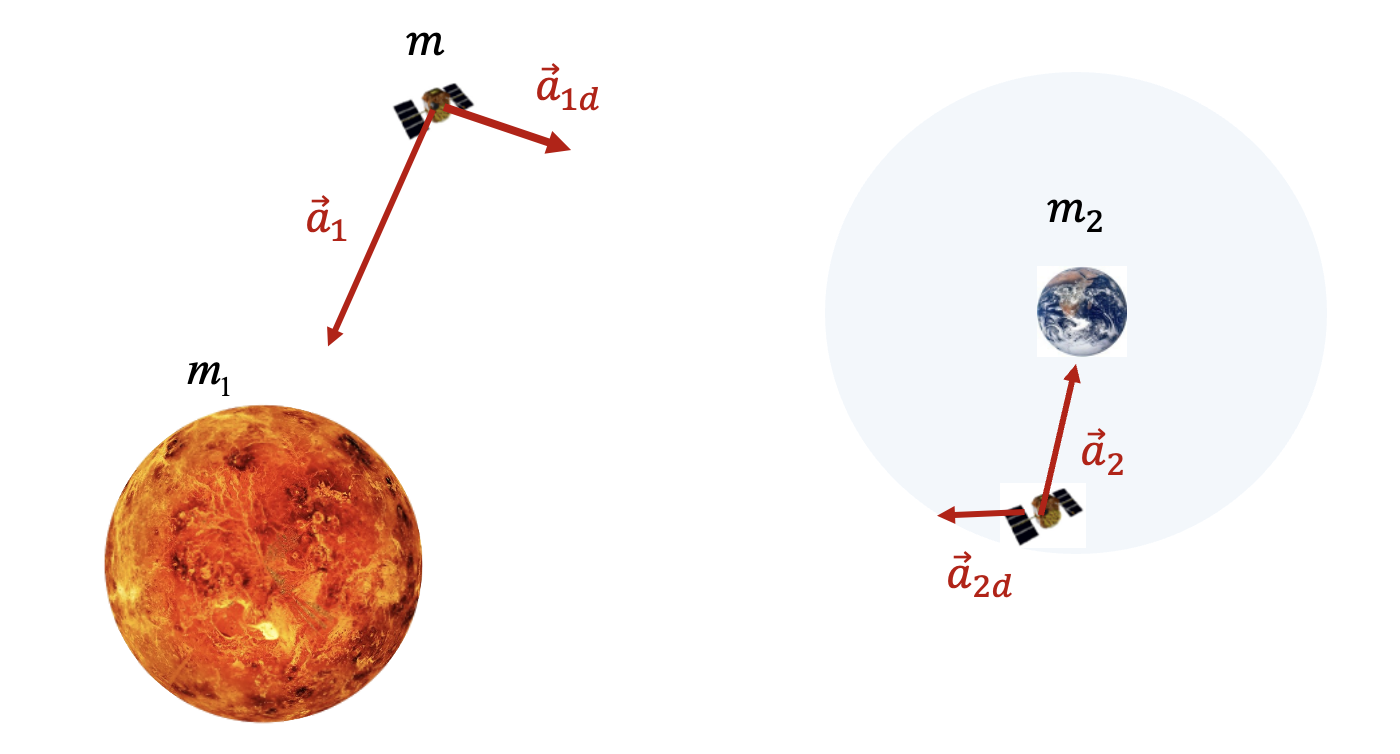
만약 두 비율이 같다면 어느 쪽의 중력도 우세하지 않는 경계면에 해당할 것이다. 이 경계면이 중력 영향권의 경계면에 해당한다.

 

\[ \begin{align} \frac{a_{1d}}{a_1} = \frac{a_{2d}}{a_2} \tag{27} \end{align} \]

 

두 질점의 질량이 \(m_1 ≫ m_2 \) 라면 \( \frac{r}{r_{21}} ≪1 \) 로 가정할 수 있으므로, 식 (25)와 (26)을 식 (27)에 대입하면 다음과 같이 근사화 된다.

 

\[ \begin{align} \frac{r}{r_{21}} \approx \left( \frac{m_2 (m_2+m)}{m_1 (m_1+m) } \right)^{\frac{1}{5}} (1+3 \cos^2 \gamma )^{-\frac{1}{10}} \tag{28} \end{align} \]

 

위 식에서 \(m_1≫m_2≫m \) 이고, \((1+3 \cos^2 \gamma )^{\frac{1}{10}} \le 1.15\) 이므로 식 (28)은 다음과 같이 더 근사화 할 수 있다.

 

\[ \begin{align} \frac{r}{r_{21}} \approx \left( \frac{m_2}{m_1} \right)^{\frac{2}{5}} \tag{29} \end{align} \]

 

\(m_1, \ m_2, \ m\) 을 각각 태양, 행성, 우주비행체라고 하면, \(r\) 은 행성의 중력 영향권의 반지름 \(R_{SOI}\) 이고, \(r_{21}\) 은 행성의 공전 반지름 \(r_{planet}\), \(m_1\)은 태양의 질량 \(M_{sun}\), \(m_2\) 는 행성의 질량 \(M_{planet}\) 이다.

 

\[ \begin{align} R_{SOI} = r_{planet} \left( \frac{M_{planet}}{M_{sun}} \right)^{\frac{2}{5}} \tag{30} \end{align} \]

 

행성의 중력 영향권 안에서는 행성의 중력이 우세하며 중력 영향권 밖에서는 태양의 중력이 우세하다고 볼 수 있다.

참고로 지구의 중력 영향권의 반지름은 \(925,000 km\) 로서 지구 반지름의 약 145배이며, 지구에서 태양까지의 거리 \(149,600,000 km\) 의 0.6% 에 해당한다.

만약 3개의 질점이 지구와 달, 우주비행체라고 한다면 식 (29)는 정확하지 않은 근사식이 된다. 왜냐하면 달의 질량이 상당하여 \(m_1≫m_2\) 라고 가정할 수 없고 따라서 \( \frac{r}{r_{21}} ≪1\) 라고 할 수 없기 때문이다. 이 때는 식 (27)에서 (28)을 유도할 때 고차항까지 더 고려할 필요가 있다.