다중 슈팅방법 (Multiple Shooting Method)

다음과 같은 비선형 미분방정식이 있다.

 

$$\begin{array}{}\text{(1)}& \dot{\mathbf{x}}(t)=\mathbf{f}(\mathbf{x}(t))\end{array}$$

 

여기서 초기값 $\mathbf{x}(t_0)$ 는 일부만 주어지거나 또는 주어지지 않았다고 가정한다. 대신 최종 시간 $t_f$ 에서 경계값 ${\mathbf{x}}_f$ 가 주어졌다고 가정한다. 이와 같은 경계값 문제의 경우 초기값이 다 주어지지 않았으므로 시간 전파를 통해 수치적분을 수행할 수가 없다.

슈팅방법(shooting method)은 경계값 문제를 초기값 문제로 바꾸어 푼다 (https://pasus.tistory.com/276). 주어지지 않은 초기값을 적당히 추정한 다음에 수치적분하여 시간이 $t_f$ 일 때 $\mathbf{x}(t_f)$ 를 ${\mathbf{x}}_f$ 와 비교한다. 오차가 있다면 그 오차를 바탕으로 초기값 $\mathbf{x}(t_0)$ 를 다른 값으로 조정하고 다시 이 값을 초기값 삼아 다시 수치적분한다. 이것을 $\mathbf{x}(t_f)={\mathbf{x}}_f$ 가 될 때까지 반복하는 방법이다.

대부분의 경우 이와 같은 방법으로 경계값 문제를 효과적으로 풀 수 있다 (https://pasus.tistory.com/328). 하지만 식 (1)의 미분방정식이 매우 비선형적이거나 불안정할 경우 초기 추정값 $\mathbf{x}(t_0)$ 에 매우 민감하여 실제 해와 약간만 벗어난 초기값을 선택하더라도 특이점이 발생하거나 발산할 수 있다. 또한 수치적분 구간이 매우 긴 경우에도 최종값이 초기값의 작은 변화에도 매우 크게 변할 수 있다. 이런 경우에는 슈팅방법으로 수치 해를 구하기가 매우 어렵거나 불가능해진다.

 

 

이 문제를 슈팅방법 구조 내에서 해결하기 위한 방안으로 다중 슈팅방법(multiple shooting method)이 있다. 이 방법의 기본 아이디어는 초기값 문제의 적분 시간 구간을 줄이는 것이다. 전체 시간 구간을 여러 개의 작은 구간으로 나누고 각각의 작은 시간 구간에 대해서 슈팅방법을 적용하여 전체 시간 구간에서의 해를 구하는 방법이다. 즉 초기 시간에서만 슈팅하는 것이 아니고 전체 시간 구간 내의 여러 싯점에서 여러 번 슈팅하는 것이다. 대신 각 시간 구간의 경계 지점에서 이전 궤적과의 연속성을 만족해야 하는 조건(매칭조건)이 필요하다. 다중 슈팅방법은 단일 슈팅방법에 비해 수치 안정성을 크게 개선했다.

 

 

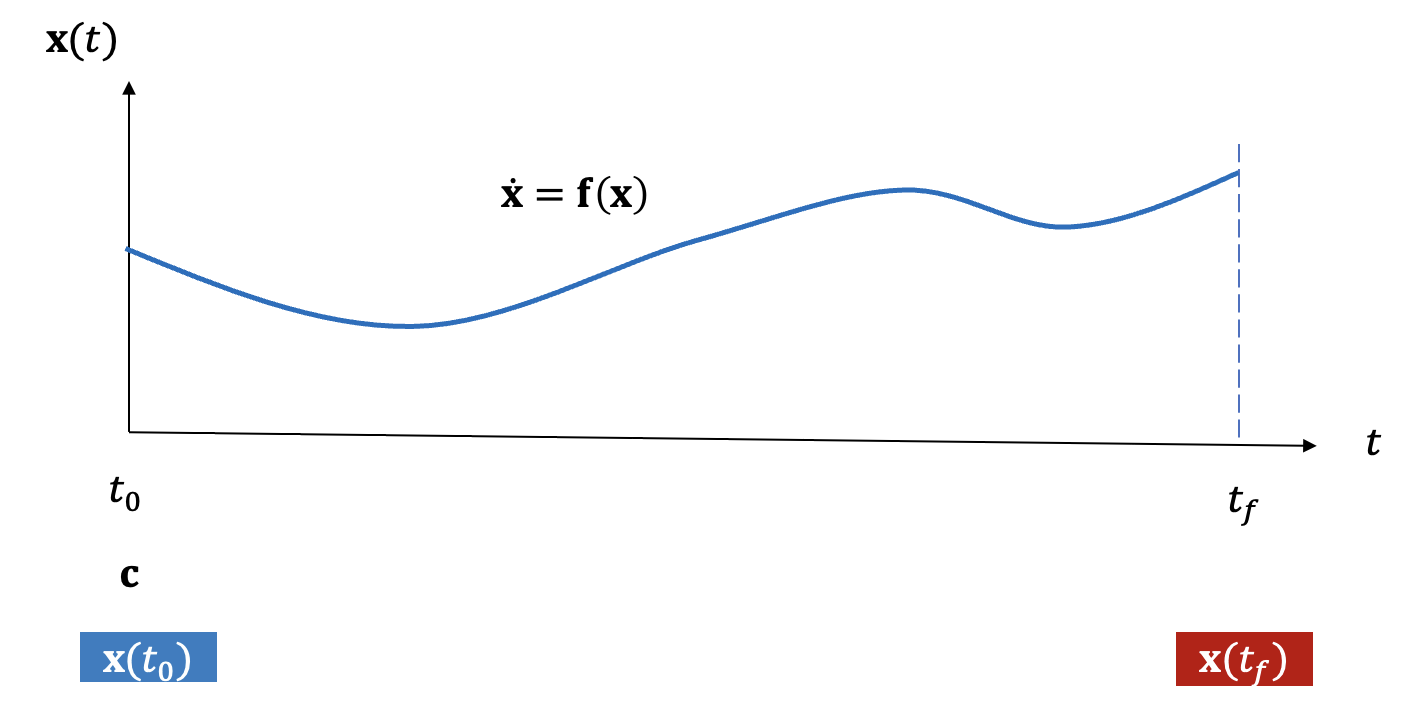
다중 슈팅방법을 설명하기 전에, 단일 슈팅방법과의 비교를 위해 먼저 단일 슈팅방법에 대해서 설명한다.

식 (1)의 경계 조건이 다음과 같이 주어졌다고 가정한다.

 

$$\begin{array}{}\text{(2)}& \mathbf{g}(\mathbf{x}(t_0),\mathbf{x}(t_f))=0\end{array}$$

 

식 (2)에 의하면 경계조건은 초기시간 $t_0$ 에서의 초기값 $\mathbf{x}(t_0)$ 과 최종시간 $t_f$ 에서의 최종값 $\mathbf{x}(t_f)$ 의 함수로 주어진다.

단일 슈팅방법은 식 (2)를 만족하도록 식 (1)의 초기값 $\mathbf{c}$ 를 구하는 것이다. 초기값이 $\mathbf{c}$ 일 때 식 (1)의 수치 해를 다음과 같이 표기한다.

 

$$\begin{array}{}\text{(3)}& \mathbf{x}(t)=\mathbf{x}(t;\mathbf{c})\end{array}$$

 

그러면 경계조건 식 (2)를 다음과 같이 표기할 수 있다.

 

$$\begin{array}{}\text{(4)}& \mathbf{h}(\mathbf{c})=\mathbf{g}(\mathbf{c},\mathbf{x}(t_f;\mathbf{c}))=0\end{array}$$

 

식 (4)에서 함수 $\mathbf{h}(\mathbf{c})$ 를 도입한 이유는 경계조건이 이제 초기값 $\mathbf{c}$ 만의 함수가 되었다는 것을 명확히 하기 위해서다.

 

 

식 (4)를 뉴톤-랩슨(Newton Raphson) 반복법으로 풀면 다음과 같다.

 

$$\begin{array}{}\text{(5)}& {\mathbf{c}}^{(i+1)}={\mathbf{c}}^{(i)}-{\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}^{-1}\mathbf{h}({\mathbf{c}}^{(i)}),i=1,2,...\end{array}$$

 

여기서 위첨자 $(i)$ 는 $i$ 번째 반복횟수를 나타내며 자코비안 ${\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}$ 는 식 (4)에 의해서 다음과 같다.

 

$$\begin{array}{r}{\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}={\left(\frac{d\mathbf{g}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}\end{array}$$

 

 

 

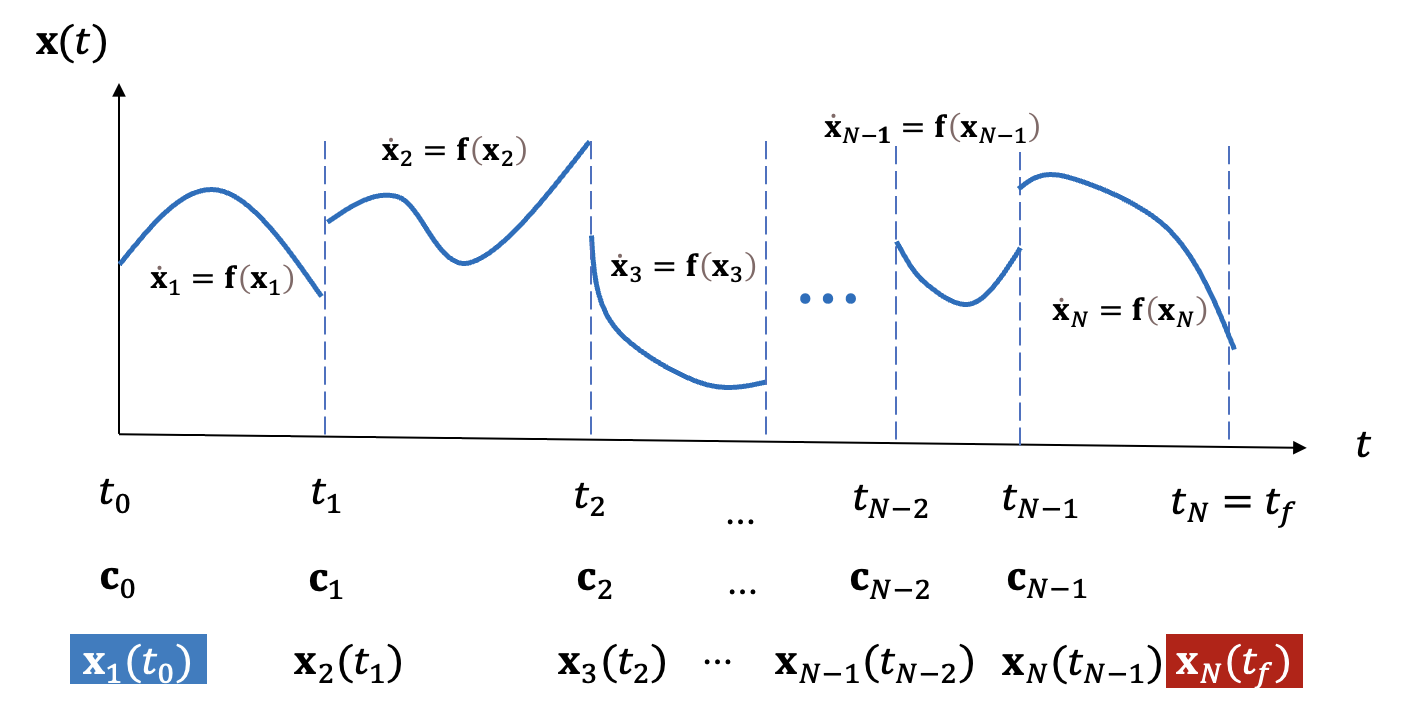
다중 슈팅방법에서는 전체 시간 구간을 다음과 같이 $N$ 개로 나눈다. 각 분할점 또는 노드는 적절히 분포시킨다.

 

$$\begin{array}{}\text{(7)}& t_0<t_1<t_2<\cdots <t_{N-1}<t_N=t_f\end{array}$$

 

식 (7)로 주어진 시간 구간에서 미분방정식 (1)의 초기값 문제는 다음과 같다.

 

$$\begin{array}{r}\text{(8)}& & {\dot{\mathbf{x}}}_n(t)=\mathbf{f}({\mathbf{x}}_n(t)),t_{n-1}\le t\le t_n\\ & {\mathbf{x}}_n(t_{n-1})={\mathbf{c}}_{n-1},n=1,2,...,N\end{array}$$

 

여기서 ${\mathbf{c}}_{n-1}$ 은 시간 $t_{n-1}$ 에서 미분방정식 (8)의 초기값이다.

 

 

식 (8)의 수치 해를 다음과 같이 표기한다.

 

$$\begin{array}{}\text{(9)}& \mathbf{x}(t)={\mathbf{x}}_n(t;{\mathbf{c}}_{n-1}),t_{n-1}\le t\le t_n,n=1,2,...,N\end{array}$$

 

그러면 경계조건 식 (2)는 다음과 같이 표기할 수 있다.

 

$$\begin{array}{}\text{(10)}& \mathbf{g}({\mathbf{c}}_0,{\mathbf{x}}_N(t_f;{\mathbf{c}}_{n-1}))=0\end{array}$$

 

여기서 시간 구간을 여러 개로 나누었기 때문에 전체 시간 구간에서 미분방정식 (1)의 해가 연속성을 가지기 위해서는 각 노드점에서 다음과 같이 매칭조건(matching condition)을 만족해야 한다.

 

$$\begin{array}{}\text{(11)}& {\mathbf{x}}_n(t_n;{\mathbf{c}}_{n-1})={\mathbf{c}}_n,n=1,2,...,N-1\end{array}$$

 

 

 

식 (10)의 경계조건과 식 (11)로 주어지는 매칭조건을 구속조건으로 통합하면 다음과 같이 표현할 수 있다.

 

$$\begin{array}{}\text{(12)}& \mathbf{h}(\mathbf{c})=\left[\begin{array}{c}{\mathbf{x}}_1(t_1;{\mathbf{c}}_0)-{\mathbf{c}}_1\\ {\mathbf{x}}_2(t_2;{\mathbf{c}}_1)-{\mathbf{c}}_2\\ ⋮\\ {\mathbf{x}}_{N-1}(t_{N-1};{\mathbf{c}}_{N-2})-{\mathbf{c}}_{N-1}\\ \mathbf{g}({\mathbf{c}}_0,{\mathbf{x}}_N(t_N;{\mathbf{c}}_{N-1}))\end{array}\right]=0\end{array}$$

 

여기서 $\mathbf{c}$ 는 각 노드점에서의 초기값으로 구성된 벡터로서 다음과 같다.

 

$$\begin{array}{}\text{(13)}& \mathbf{c}=\left[\begin{array}{c}{\mathbf{c}}_0\\ {\mathbf{c}}_1\\ {\mathbf{c}}_2\\ ⋮\\ {\mathbf{c}}_{N-1}\end{array}\right]\end{array}$$

 

다중 슈팅방법은 식 (12)를 만족하는 $\mathbf{c}$ 를 구하는 것으로서 뉴톤-랩슨(Newton Raphson) 반복법으로 풀면 다음과 같다.

 

$$\begin{array}{}\text{(14)}& {\mathbf{c}}^{(i+1)}={\mathbf{c}}^{(i)}-{\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}^{-1}\mathbf{h}({\mathbf{c}}^{(i)}),i=1,2,...\end{array}$$

 

여기서 자코비안 ${\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}$ 는 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(15)}& {\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}=\left[\begin{array}{cccccc}{\left(\frac{\partial {\mathbf{x}}_1(t_1)}{\partial {\mathbf{c}}_0}\right)}_{{\mathbf{c}}_0^{(i)}}& -I& 0& & 0& 0\\ 0& {\left(\frac{\partial {\mathbf{x}}_2(t_2)}{\partial {\mathbf{c}}_1}\right)}_{{\mathbf{c}}_1^{(i)}}& -I& & 0& 0\\ 0& 0& {\left(\frac{\partial {\mathbf{x}}_3(t_3)}{\partial {\mathbf{c}}_2}\right)}_{{\mathbf{c}}_2^{(i)}}& \ddots & 0& 0\\ & & & \ddots & & \\ 0& 0& 0& & {\left(\frac{\partial {\mathbf{x}}_{N-1}(t_{N-1})}{\partial {\mathbf{c}}_{N-2}}\right)}_{{\mathbf{c}}_{N-2}^{(i)}}& -I\\ {\left(\frac{\partial \mathbf{g}}{\partial {\mathbf{c}}_0}\right)}_{{\mathbf{c}}_0^{(i)}}& 0& 0& & 0& {\left(\frac{\partial \mathbf{g}}{\partial {\mathbf{c}}_{N-1}}\right)}_{{\mathbf{c}}_{N-1}^{(i)}}\end{array}\right]\end{array}$$

 

자코비안 ${\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}$ 는 다시 자코비안 ${\left(\frac{\partial {\mathbf{x}}_n(t_n)}{\partial {\mathbf{c}}_{n-1}}\right)}_{{\mathbf{c}}_{n-1}^{(i)}}$ 과 ${\left(\frac{\partial \mathbf{g}}{\partial {\mathbf{c}}_0}\right)}_{{\mathbf{c}}_0^{(i)}}$ 및 ${\left(\frac{\partial \mathbf{g}}{\partial {\mathbf{c}}_{N-1}}\right)}_{{\mathbf{c}}_{N-1}^{(i)}}$ 으로 구성되어 있다. 식 (14)에 의하면 $\mathbf{c}$ 를 업데이트하기 위해서는 자코비안 ${\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}$의 역행렬을 계산해야 한다. 노드수가 증가할 수록 식 (15)의 자코비안 행렬의 차원이 증가하여 역행렬 계산에 부담이 따를 수 있지만, 식 (15)에 의하면 자코비안 ${\left(\frac{d\mathbf{h}}{d\mathbf{c}}\right)}_{{\mathbf{c}}^{(i)}}$는 대부분의 구성요소가 $0$ 인 행렬이므로 가우스 소거법 등의 알고리즘을 사용할 수 있다.