미분보정 (Differential Correction)

미분보정(differential correction)은 슈팅방법(shooting method)으로도 불린다. 기본적으로 미분방정식의 경계값 문제(boundary value problem)를 초기값 문제(initial value problem)로 바꾸어 해를 구하는 방법이다.

다음과 같은 비선형 미분방정식이 있다.

 

$$\begin{array}{}\text{(1)}& \dot{\mathbf{x}}(t)=\mathbf{f}(\mathbf{x}(t))\end{array}$$

 

여기서 초기값 $\mathbf{x}(t_0)$ 은 일부만 주어지거나 또는 주어지지 않았다고 가정한다. 대신 정해진 시간 $t_f$ 에서 경계값 ${\mathbf{x}}_d$ 가 주어졌다고 가정한다. 문제는 시간 $t_f$ 에서 $\mathbf{x}(t_f)={\mathbf{x}}_d$ 가 되도록 초기값 $\mathbf{x}(t_0)$ 을 구하는 것이다.

 

 

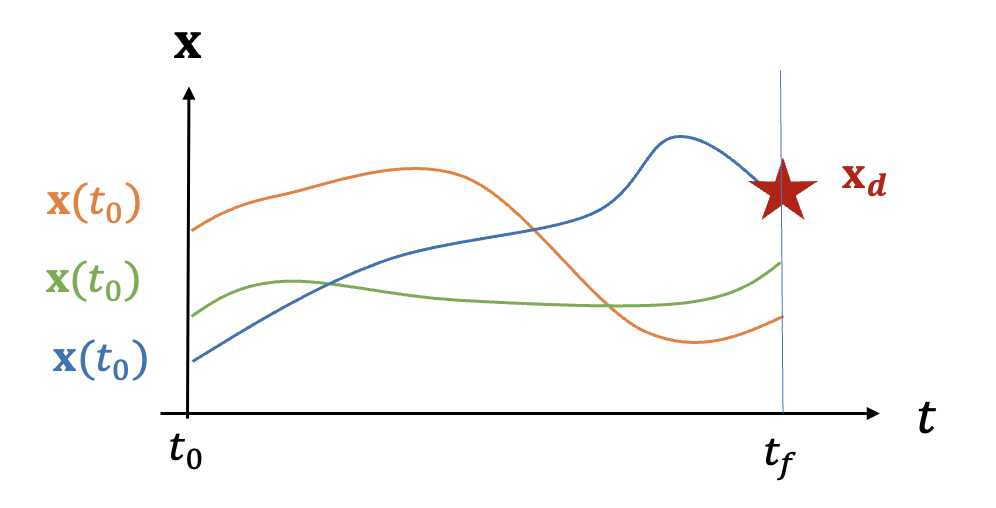
경계값 문제의 경우 초기값이 다 주어지지 않았으므로 시간 전파를 하며 수치적분을 수행할 수가 없다. 대신 주어지지 않은 초기값을 적당히 추정한 다음에 초기값 문제를 풀 듯이 순차적으로 시간 전파해야 한다. 그리고 시간이 $t_f$ 일 때 $\mathbf{x}(t_f)$ 를 ${\mathbf{x}}_d$ 와 비교해서 오차가 있다면 그 오차를 바탕으로 초기값 $\mathbf{x}(t_0)$ 를 다른 값으로 조정해 본다. 그리고 다시 이 값을 초기값 삼아 시간 전파하는 것이다. 이것을 $\mathbf{x}(t_f)={\mathbf{x}}_d$ 가 될 때까지 반복하는 방법을 미분보정 또는 슈팅방법이라고 한다.

 

 

초기값 $\mathbf{x}(t_0)$ 일 때 식 (1)의 해 또는 궤적을 $\mathbf{x}(t)$ 로 표현하자. 또한 원래 초기값에 섭동을 준 새로운 초기값 $\mathbf{x}(t_0)+\delta \mathbf{x}(t_0)$ 에서 시작된 궤적을 $\tilde{\mathbf{x}}(t)$ 로 표현하자.

 

 

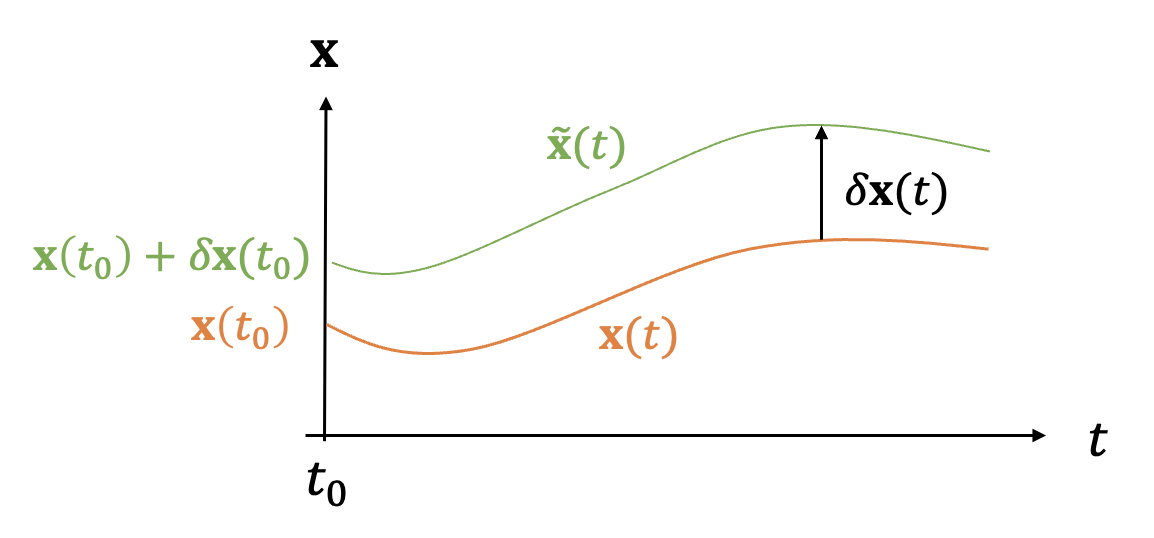
러면 두 궤적 사이의 차이는 다음과 같다.

 

$$\begin{array}{}\text{(2)}& \delta \mathbf{x}(t)=\tilde{\mathbf{x}}(t)-\mathbf{x}(t)\end{array}$$

 

만약 초기값의 섭동 $\delta \mathbf{x}(t_0)$ 가 매우 작다면 두 궤적 사이의 차이 $\delta \mathbf{x}(t)$ 도 작다고 가정할 수 있으므로 테일러 시리즈 1차항에서 절삭한 $\delta \mathbf{x}(t)$ 의 미분방정식을 다음과 같이 표현할 수 있다.

 

$$\begin{array}{r}\text{(3)}& \delta \dot{\mathbf{x}}(t)& =\dot{\tilde{\mathbf{x}}}(t)-\dot{\mathbf{x}}(t)=\mathbf{f}(\tilde{\mathbf{x}}(t))-\mathbf{f}(\mathbf{x}(t))\\ & =\mathbf{f}(\mathbf{x}(t)+\delta \mathbf{x}(t))-\mathbf{f}(\mathbf{x}(t))\\ \\ & =\mathbf{f}(\mathbf{x}(t))+{\frac{\partial \mathbf{f}}{\partial \mathbf{x}}|}_{\mathbf{x}(t)}\delta \mathbf{x}(t)+HOT-\mathbf{f}(\mathbf{x}(t))\\ \\ & \approx {\frac{\partial \mathbf{f}}{\partial \mathbf{x}}|}_{\mathbf{x}(t)}\delta \mathbf{x}(t)\\ \\ & =A(t)\delta \mathbf{x}(t)\end{array}$$

 

여기서 자코비안 $\frac{\partial \mathbf{f}}{\partial \mathbf{x}}$ 는 궤적 $\mathbf{x}(t)$ 를 따라서 계산해야 하기 때문에 시간 함수 $A(t)$ 가 된다.

식 (3)은 선형 시변(linear time-varying) 방정식이므로 다음과 같이 상태천이행렬(state transition matrix)을 이용하여 해를 구할 수 있다(https://pasus.tistory.com/274).

 

$$\begin{array}{}\text{(4)}& \delta \mathbf{x}(t)=\mathrm{\Phi }(t,t_0)\delta \mathbf{x}(t_0)\end{array}$$

 

그러면 초기값 $\mathbf{x}(t_0)+\delta \mathbf{x}(t_0)$ 로 시작한 상태변수 값이 시간 $t_f$ 에서는 다음 값이 된다.

 

$$\begin{array}{r}\text{(5)}& \tilde{\mathbf{x}}(t_f)& =\mathbf{x}(t_f)+\delta \mathbf{x}(t_f)\\ & =\mathbf{x}(t_f)+\mathrm{\Phi }(t_f,t_0)\delta \mathbf{x}(t_0)\end{array}$$

 

$\tilde{\mathbf{x}}(t_f)$ 값이 ${\mathbf{x}}_d$ 가 되는 것이 목표이므로 위 식에서 초기값의 섭동 $\delta \mathbf{x}(t_0)$ 을 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(6)}& \delta \mathbf{x}(t_0)={\mathrm{\Phi }}^{-1}(t_f,t_0)[{\mathbf{x}}_d-\mathbf{x}(t_f)]\end{array}$$

 

식 (6)에 의하면 초기값 $\mathbf{x}(t_0)$ 를 $\mathbf{x}(t_0)+\delta \mathbf{x}(t_0)$ 로 변경하면 테일러 시리즈 1차 근사의 정확도로 $\tilde{\mathbf{x}}(t_f)$ 값이 ${\mathbf{x}}_d$ 가 될 수 있음을 알 수 있다. 이것이 미분보정의 기본 프로세스이다. 즉, 시간 $t_f$ 에서 목표값 ${\mathbf{x}}_d$ 와 현재의 초기값으로 산출된 최종값 $\mathbf{x}(t_f)$ 간의 차이를 이용하여 초기값을 수정하는 것이다.

결국 다음 식으로 수정된 초기값

 

$$\begin{array}{}\text{(7)}& \mathbf{x}(t_0)\leftarrow \mathbf{x}(t_0)+{\mathrm{\Phi }}^{-1}(t_f,t_0)[{\mathbf{x}}_d-\mathbf{x}(t_f)]\end{array}$$

 

을 이용하여 위 프로세스를 반복하면 $\mathbf{x}(t_f)={\mathbf{x}}_d$ 가 되는 초기값 $\mathbf{x}(t_0)$ 를 계산해 낼 수 있다.

우주역학 분야에서는 주로 섭동력을 받는 램버트 문제(Lambert's problem)나 또는 삼체문제에서 주기궤도(periodic orbit)를 설계하는 데에 미분보정이 사용되고 있다.