가우시안 쿼드래처(Gaussian quadrature)는 구간 \([-1, 1]\) 에서 어떤 함수 \(f(\tau)\) 의 적분값을 적분 구간내의 특정 지점에서의 함수값의 가중치 합으로 계산하는 수치적분 방법이다.
\[ \int_{-1}^1 f(\tau) \ d \tau \approx \sum_{i=1}^N w_i f(\tau_i) \tag{1} \]
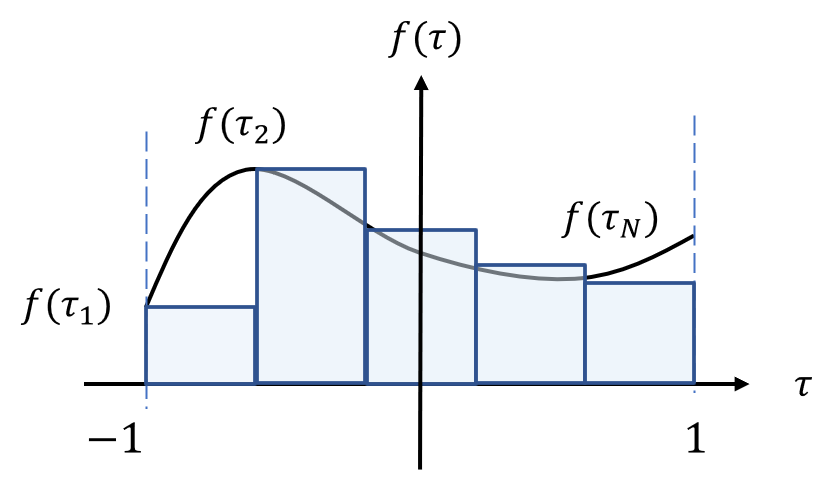
여기서 적분 구간내의 특정 지점인 \(\tau =\tau_1, \tau_2, ..., \tau_N\) 을 쿼드래처 포인트라고 하고, \(w_i\) 를 쿼드래처 포인트의 가중치(weighting)이라고 한다. 가우시안 쿼드래처의 정확도는 쿼드래처 포인트의 갯수와 점 사이의 간격에 달려있다.
함수 \(f(\tau)\) 를 \((N-1)\) 차 라그랑지 보간 다항식으로 근사화한다고 하면, 식 (1)은 다음과 같이 된다.
\[ \begin{align} \int_{-1}^1 f(\tau) \ d \tau & \approx \int_{-1}^1 \sum_{i=1}^N f(\tau_i ) L_i (\tau) \ d \tau \tag{2} \\ \\ &= \sum_{i=1}^N f(\tau_i ) \int_{-1}^1 L_i (\tau) \ d \tau \end{align} \]
식 (1)과 (2)를 비교해 보면, 가중치는 다음과 같음을 알 수 있다.
\[ w_i= \int_{-1}^1 L_i (\tau) \ d \tau = \int_{-1}^1 \prod_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \frac{ \tau-\tau_k}{\tau_i-\tau_k } \ d \tau \tag{3} \]
쿼드래처 포인트로는 주로 LGL, LG, 또는 LGR 포인트가 사용된다.
LGL 포인트가 사용될 경우 가중치는 다음과 같이 주어진다.
\[ w_i= \begin{cases} \frac{2}{ N(N-1) [P_{N-1} (\tau_i )]^2 }, & i=2, ..., N-1 \\ \frac{2}{N(N-1)}, & i=1, N \end{cases} \tag{4} \]
여기서 \(P_{N-1} (\tau)\) 은 \((N-1)\) 차 르장드르 다항식이다.
LG 포인트가 사용될 경우 가중치는 다음과 같이 주어진다.
\[ w_i= \frac{2}{ (1-\tau_i^2 ) \left[ \dot{P}_N (\tau_i ) \right]^2 }, \ \ \ 1= 1, 2, ..., N \tag{5} \]
LGR 포인트가 사용될 경우 가중치는 다음과 같이 주어진다.
\[ w_i= \begin{cases} \frac{1}{ (1-\tau_i) \left[ \dot{P}_{N-1} (\tau_i ) \right]^2 }, & i=2, ..., N \\ \frac{2}{N^2}, & i=1 \end{cases} \tag{6} \]
다음은 쿼드래처 포인트가 각각 LGL, LG, LGR 포인트일 때, 가우시안 쿼드래처 가중치를 계산하는 매트랩 함수의 코드이다.
function weights = GaussianQuadrature(n,ptype)
%
% quadrature weights of n Gaussian quadrature points
% weights = GaussianQuadrature(n,ptype)
%
% Needs GaussPoints.m LegendrePoly.m
%
% input: n (quadrature point number=interpolating point number of Lagrange poly)
% ptype (quadrature point type: LGL, LG, LGR)
% LG - Legendre-Gauss points
% LGR - Legendre-Gauss-Radau points
% LGL - Legendre-Gauss-Lobatto points
% output: quadrature weights
%
% coded by St.Watermelon
%
if n<2
weights=0;
return;
end
switch ptype
case 'LG'
lgp=GaussPoints(n,'LG');
lpd=LegendrePolyDerivative(n);
lpdval=polyval(lpd,lgp);
weights=2./((1-lgp.^2).*(lpdval).^2);
return;
case 'LGR'
lgrp=GaussPoints(n,'LGR');
lpd=LegendrePolyDerivative(n-1);
lpdval=polyval(lpd,lgrp(2:end));
weights=1./((1-lgrp(2:end)).*(lpdval).^2);
weights=[2/n^2;weights];
return
case 'LGL'
lglp=GaussPoints(n,'LGL');
lp=LegendrePoly(n-1);
lpval=polyval(lp,lglp(2:end-1));
weights=2./(n*(n-1).*(lpval).^2);
weights=[2/(n*(n-1));weights;2/(n*(n-1))];
return;
otherwise
weights=0;
return;
end
function Pnd=LegendrePolyDerivative(n)
% derivative of Legendre polynomials
Pn=LegendrePoly(n);
pl2=[];
for kk=1:(length(Pn)-1)
pl2=[pl2 (length(Pn)-kk)*Pn(kk)];
end
Pnd=pl2;
그러면 가우시안 쿼드래처를 이용하여 실제로 수치적분을 해보자. 다음 적분식이 있다.
\[ \int_{-1}^1 f(t) \ dt = \int_{-1}^1 \left( 1+\frac{t}{3}-t^2 \right) \ dt \tag{7} \]
위 식은 해석적으로 풀 수 있는데 적분값은 \( 4/3=1.3333\) 이다. 이제 각각 3개의 LGL, LG, LGR 쿼드래처 포인트를 이용하여 위 식을 수치적분 해본다.
먼저 LGL 포인트와 가중치는 다음과 같다.
\[ \begin{align} & t_1=-1, \ t_2=0, \ t_3=1 \\ \\ & w_1=0.3333, \ w_2=1.3333, \ w_3=0.3333 \end{align} \]
따라서 수치 적분값은 다음과 같다.
\[ \sum_{i=1}^3 w_i f(t_i) =0.3333 f(-1)+1.3333f(0)+0.3333f(1)=1.3333 \]
이번에는 LG 포인트와 가중치를 이용한 수치적분이다.
\[ \sum_{i=1}^3 w_i f(t_i) =0.5556f(-0.7746)+0.8889f(0)+0.5556f(0.7746)=1.3333 \]
LGR 포인트와 가중치를 이용한 수치 적분값은 다음과 같다.
\[ \sum_{i=1}^3 w_i f(t_i) =0.2222f(-1)+1.0250f(-0.2899)+0.7528f(0.6899)=1.3333 \]
따라서 세 경우 모두 수치적분 값이 정답과 일치함을 알 수 있다.
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-7] 유사 스펙트럴 방법 예제 (0) | 2022.04.24 |
|---|---|
| [PSOC-6] 유사 스펙트럴 방법 (Pseudospectral Method) (0) | 2022.04.23 |
| [PSOC-4] 라그랑지 보간 다항식 (0) | 2021.12.17 |
| [PSOC-3] 가우스 포인트 (Gauss Points) (0) | 2021.12.16 |
| [PSOC-2] 르장드르 다항식 (Legendre Polynomials) (0) | 2021.12.15 |




댓글