\(N\) 개의 임의의 점 \(t_i\) 에서 함수 \(f(t)\) 의 값 \(f(t_i)\) 가 주어졌을 때,
\(N\) 개의 점 \(f(t_i)\) 를 지나는 \((N-1)\) 차 라그랑지 보간 다항식(Lagrange interpolation polynomials) \(p(t)\) 는 다음과 같이 주어진다.
\[ f(t) \approx p(t) = \sum_{i=1}^N f(t_i ) L_i (t) \tag{1} \]
여기서 \(t_i\) 를 보간점(interpolating point)라고 한다. 또한 \(L_i (t)\) 를 \((N-1)\) 차 라그랑지 기저 다항식(Lagrange basis polynomials) 또는 라그랑지 다항식이라고 하며 다음과 같이 정의한다.
\[ L_i (t)= \prod_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \frac{t-t_k}{t_i-t_k} \tag{2} \]
라그랑지 기저 다항식의 갯수는 보간점의 갯수와 같다. 아래 그림은 4개의 보간점에서 데이터셋 \((-9, 5)\), \( (-4, 2)\), \( (-1, -2)\), \( (7, 9)\) 가 주어졌을 때, 기저 다항식 \(L_1 (t), ..., L_4 (t)\) 와 보간 다항식 \(p(t)\) 를 그린 것이다.
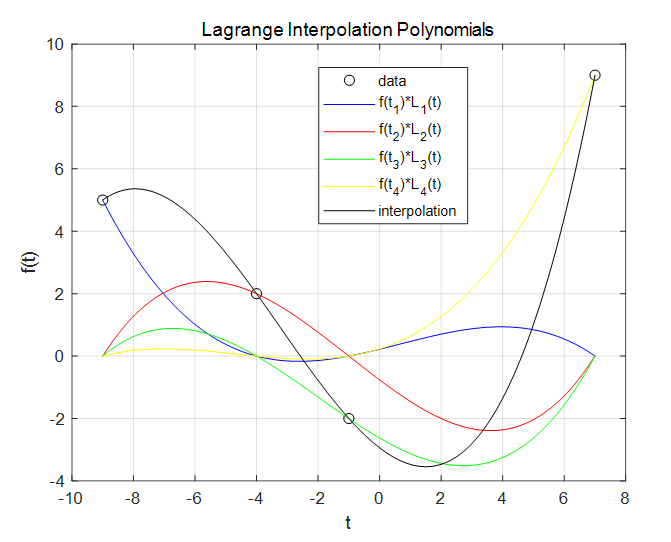
라그랑지 기저 다항식의 정의에 의해서 \(L_i (t_i )=1\) 이고, \(i \ne j\) 이면 \(L_i (t_j )=0\) 이다. 위 그림에서도 이런 사실을 확인할 수 있다. 여기서 \(t_j\) 는 보간점 중의 한 점이다.
다음은 라그랑지 다항식의 계수를 구하는 매트랩 함수의 코드이다.
function [p, Li] = LagrangePoly(dataset,t)
%
% Lagrange interpolation polynomials
% [p, Li] = LagrangePoly(dataset,t)
%
% want p(t) ~ f(t)
% given (t1,f(t1)), (t2,f(t2)), ..., (tn,f(tn))
% within time intervals t0 <= t <= tf
%
% input: dataset=[t_i f(t_i)], i=1,...,N
% t (evaluation intervals)
% output: polynomial function p(t)
% Lagrange polynomials Li(t)
%
% coded by St.Watermelon
%
spoint=dataset(:,1); % interpolating points
fi=dataset(:,2); % f(t) at interpolating points
p=zeros(length(t),1);
N=length(spoint); % number of interpolating points
for ii=1:N
Li{ii}=ones(length(t),1); % Lagrange polynomials
for kk=1:N
if kk~=ii
Li{ii}=Li{ii} ...
.*((t-spoint(kk))./(spoint(ii)-spoint(kk)));
end
end
p=p+Li{ii}.*fi(ii); % p(t)
end
라그랑지 보간 다항식에서 보간점의 선택은 근사해의 정확도에 큰 영향을 미친다. 보간점의 간격이 일정하면 다항식을 이용한 보간(interpolation)에서 룽게현상(Runge's phenomenon)이라는 문제를 일으킨다. 룽게현상이란 보간식으로 산출하는 값이 참값을 중심으로 진동하는 현상을 말한다. 룽게현상은 보간점의 개수가 증가할수록, 또한 보간 구간의 양 끝단으로 갈수록 더 심해진다.
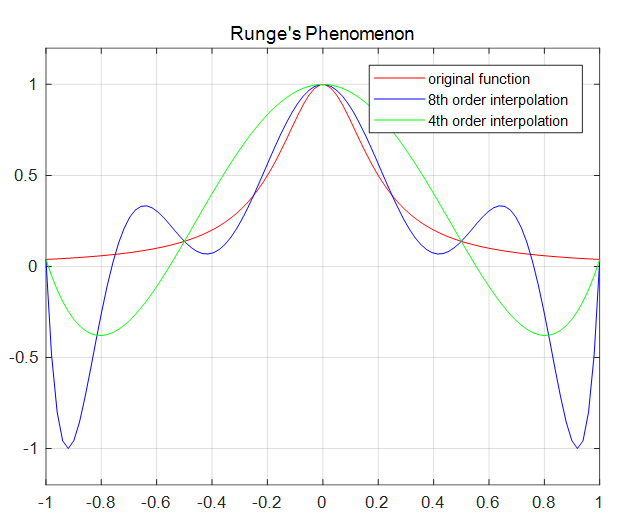
따라서 점들 사이의 간격이 서로 다른 보간점을 이용하는데, 주로 LGL, LG, 또는 LGR 포인트가 사용되고 있다. LGL, LG, LGR 포인트는 \([-1, 1]\) 구간에서 정의된다는 점에 주의하자.
다음 그림은 각각 LGL, LG, LGR 포인트를 보간점으로 하는 8차 라그랑지 보간 다항식과 실제 함수의 그림을 비교한 것이다. 룽게현상이 확실히 준 것을 알 수 있다. LGR 포인트는 LGL, LG 포인트와는 달리 보간점의 분포가 비대칭이므로 보간 다항식의 결과가 실제 함수와 달리 비대칭적이다.
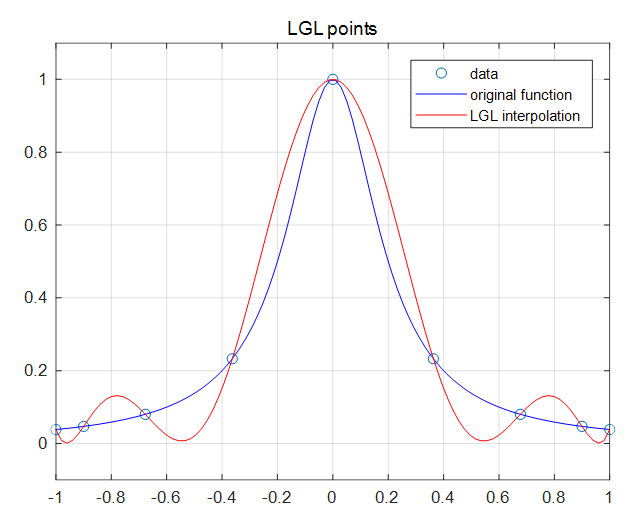
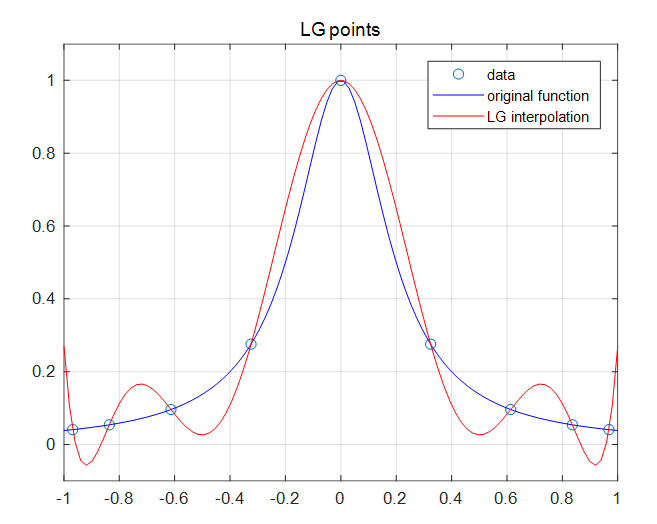

라그랑지 기저 다항식의 미분 \( \dot{L}_i (t)\) 은 다음과 같다.
\[ \begin{align} \dot{L}_i (t) &= \frac{d}{dt} \prod_{\begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \frac{t-t_k}{t_i-t_k } \tag{3} \\ \\ &= \frac{1}{t_i-t_1} \prod_{\begin{matrix} m=1 \\ m \ne i,1 \end{matrix}}^N \frac{t-t_m}{t_i-t_m } + \frac{1}{t_i-t_2} \prod_{\begin{matrix} m=1 \\ m \ne i,2 \end{matrix}}^N \frac{t-t_m}{t_i-t_m } \\ \\ & \ \ \ \ + ... + \frac{1}{t_i-t_N} \prod_{\begin{matrix} m=1 \\ m \ne i,N \end{matrix}}^N \frac{t-t_m}{t_i-t_m } \\ \\ &= \sum_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \left[ \frac{1}{t_i-t_k } \prod _{ \begin{matrix} m=1 \\ m \ne i,k \end{matrix}}^N \frac{t-t_m}{t_i-t_m } \right] \end{align} \]
보간점 \(t=t_j\) 에서 라그랑지 다항식의 미분 \(\dot{L}_i (t_j )\) 을 계산하면, \(i=j\) 인 경우에는
\[ \begin{align} \dot{L}_i (t_i ) &= \sum_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \left[ \frac{1}{t_i-t_k} \prod_{ \begin{matrix} m=1 \\ m \ne i,k \end{matrix}}^N \frac{t_i-t_m}{t_i-t_m } \right] \tag{4} \\ &= \sum_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \frac{1}{t_i-t_k } \end{align} \]
이 되고, \(i \ne j\) 인 경우에는
\[ \dot{L}_i (t_j ) = \sum_{ \begin{matrix} k=1 \\ k \ne i \end{matrix}}^N \left[ \frac{1}{t_i-t_k} \prod_{ \begin{matrix} m=1 \\ m \ne i,k \end{matrix}}^N \frac{t_j-t_m}{t_i-t_m } \right] \tag{5} \]
이다. 여기서 \(k=j\) 를 제외하고는 오른쪽항의 곱셈이 모두 \(0\) 이 되므로,
\[ \begin{align} \dot{L}_i (t_j ) &= \frac{1}{t_i-t_j} \prod_{ \begin{matrix} m=1 \\ m \ne i,j \end{matrix}}^N \frac{t_j-t_m}{t_i-t_m } \tag{6} \\ \\ &= \frac{ \prod_{ m=1, m \ne j }^N (t_j-t_m) }{ (t_i-t_j ) \prod_{ m=1, m \ne i }^N (t_i-t_m) } \end{align} \]
\(t=t_j\) 에서 계산한 라그랑지 다항식의 미분을 행렬로 나타내고 미분행렬(differentiation matrix)이라고 정의한다.
\[ \left[ D_{ji} \right] = \dot{L}_i (t_j ) = \begin{bmatrix} \dot{L}_1 (t_1) & \dot{L}_2 (t_1) & ... & \dot{L}_N (t_1) \\ \dot{L}_1 (t_2) & \dot{L}_2 (t_2) & ... & \dot{L}_N (t_2) \\ \vdots & \vdots & \ddots & \vdots \end{bmatrix} \tag{7} \]
유사 스펙트럴 방법(pseudospectral method)을 이용한 최적제어에서는 콜로케이션 포인트에서 미분값이 계산된다. 콜로케이션 포인트로는 주로 LGL, LG, 또는 LGR 포인트가 사용되며, 보간점으로는 LGL 포인트, LG 포인트에 \(-1\) 점을 추가한 점, 또는 LGR 포인트에 \(+1\) 점을 추가한 점이 사용된다.
다음은 라그랑지 다항식의 미분을 \(t=t_j\) 에서 계산하는 매트랩 함수의 코드이다. 여기서 미분값이 계산되는 점(evaluation point)은 보간점의 전부 또는 일부로 구성되는 점이다.
function Dji = LagrangePolyDerivative(eval_point,int_point)
%
% Differentiation of Lagrange basis polynomials at t_j
% Dji = LagrangePolyDerivative(eval_point,int_point)
%
% input: evaluation point = {t_1, t_2,..., t_N}
% mostly given by collocation point
% eval_point= t_j
% interpolation point = {t_0, eval_point, t_N+1} (-1<= t <= 1)
% always includes evaluation point
% int_point = t_i
% if t_1=-1, t_0=[]
% if t_N=1, t_N+1=[]
% output: differentiation matrix Dji = Ld_i (t_j)
%
% coded by St.Watermelon
%
atol = 1e-7; % tolerance
iNo=length(int_point);
eNo=length(eval_point);
if eNo > iNo
Dji=0;
return;
end
Dji=zeros(eNo,iNo);
for jj = 1: eNo
for ii = 1:iNo
if abs(eval_point(jj)-int_point(ii))< atol % if i==j
sum = 0;
for kk = 1:iNo
% if ii~=kk
if abs(int_point(ii)-int_point(kk))> atol
sum = sum + 1/(int_point(ii)-int_point(kk));
end
end
Dji(jj,ii) = sum;
else
mul = 1;
for mm = 1:iNo
% if ii~=mm && jj~=mm
if abs(int_point(ii)-int_point(mm))> atol ...
&& abs(eval_point(jj)-int_point(mm))> atol
mul = mul * (eval_point(jj)-int_point(mm)) ...
/(int_point(ii)-int_point(mm));
end
end
mul = mul/(int_point(ii)-eval_point(jj));
Dji(jj,ii) = mul;
end
end
end
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-6] 유사 스펙트럴 방법 (Pseudospectral Method) (0) | 2022.04.23 |
|---|---|
| [PSOC-5] 가우시안 쿼드래처 (Gaussian Quadrature) (0) | 2021.12.18 |
| [PSOC-3] 가우스 포인트 (Gauss Points) (0) | 2021.12.16 |
| [PSOC-2] 르장드르 다항식 (Legendre Polynomials) (0) | 2021.12.15 |
| [PSOC-1] 유사 스펙트럴 기반 최적제어 개요 (0) | 2021.12.15 |




댓글