가우스 포인트(Gauss points)는 \([-1, 1]\) 의 구간에서 정의되는 점들의 집합으로서 점(point)간의 간격이 서로 다르다는 특징이 있다.
가우스 포인트는 라그랑지 보간 다항식(Lagrange interpolation polynomials)의 보간점(interpolating point), 가우스 쿼드래처(Gauss quadrature)의 쿼드래처 포인트(quadrature point), 그리고 유사 스펙트럴 방법(pseudospectral method)의 콜로케이션 포인트(collocation point)로 사용된다.
가우스 포인트는 다음 3가지가 있으며, 각각 다음과 같이 정의된다.
(a) LGL (Legendre-Gauss-Lobatto) 포인트:
LGL 포인트는 \((N-1)\) 차 르장드르 다항식을 미분한 식 \(\dot{P}_{N-1} (\tau)\) 의 근(root) \((N-2)\) 개와 두 점 \(-1, +1\) 등 \(N\) 개의 점들로 구성된다.
(b) LG (Legendre-Gauss) 포인트:
LG 포인트는 \(N\) 차 르장드르 다항식 \(P_N (\tau)\) 의 근 \(N\) 개로 구성된다. LG 포인트는 두 점 \(-1,+1\) 을 포함하지 않는다.
(c) LGR (Legendre-Gauss-Radau) 포인트:
LGR 포인트는 두 개의 르장드르 다항식의 합 \(P_N (\tau)+P_{N-1} (\tau)\) 의 근 \(N\) 개로 구성된다. LGR 포인트는 \(-1\) 점을 포함하고 있다. 플립(flipped) LGR은 \(P_N (\tau)-P_{N-1} (\tau)\) 의 근 \(N\) 개로 구성되며 LGR 포인트를 거울에 비춘 상이다. 플립 LGR 포인트는 \(+1\) 점을 포함하고 있다.
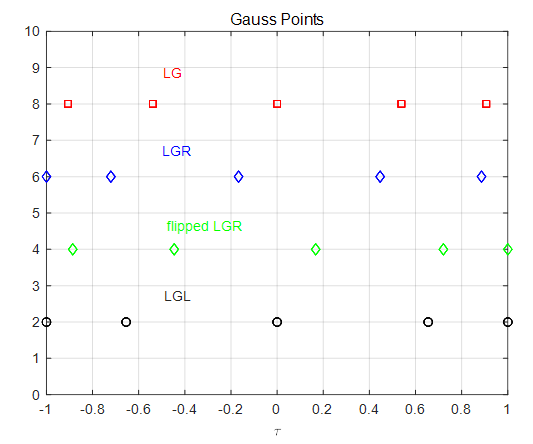
다음 그림은 각각 5개의 점들로 이루어진 가우스 포인트를 그린 것이다.
다음은 가우스 포인트를 구하는 매트랩 함수의 코드이다.
function points = GaussPoints(n,ptype)
%
% n Guassian points generation
% points = GaussPoints(n,ptype)
%
% Needs LegendrePoly.m
%
% input: n (point number)
% ptype (point type: LG, LGR, fLGR, LGL)
% LG - Legendre-Gauss points
% LGR - Legendre-Gauss-Radau points
% fLGR - flipped Legendre-Gauss-Radau points
% LGL - Legendre-Gauss-Lobatto points
% output: Gauss points
%
% coded by St.Watermelon
%
% if input point number is 0 or 1, just return
if n<2
points=0;
disp('not enough number of Gauss points');
return;
end
switch ptype
case 'LG' % Legendre-Gauss points
lg=LegendrePoly(n); % n-th Legendre polynomials
points=sort(roots(lg));
return;
case 'LGR' % Legendre-Gauss-Radau points
plN=LegendrePoly(n); % n-th Legendre polynomials
plN1=LegendrePoly(n-1); % (n-1)-th Legendre polynomials
pl=plN+[0 plN1]; % Pn + Pn-1
points=sort(roots(pl));
return
case 'fLGR' % flipped LGR
plN=LegendrePoly(n); % n-th Legendre polynomials
plN1=LegendrePoly(n-1); % (n-1)-th Legendre polynomials
pl=plN-[0 plN1]; % Pn - Pn-1
points=sort(roots(pl));
return
case 'LGL' % Legendre-Gauss-Lobatto points
plL=LegendrePoly(n-1); % (n-1)-th Legendre polynomials
pl2=[];
for kk=1:(length(plL)-1) % derivatives of Pn-1
pl2=[pl2 (length(plL)-kk)*plL(kk)];
end
points=[-1; sort(roots(pl2)); 1]; % insert -1, +1
return;
otherwise
points=0;
return;
end
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [PSOC-5] 가우시안 쿼드래처 (Gaussian Quadrature) (0) | 2021.12.18 |
|---|---|
| [PSOC-4] 라그랑지 보간 다항식 (0) | 2021.12.17 |
| [PSOC-2] 르장드르 다항식 (Legendre Polynomials) (0) | 2021.12.15 |
| [PSOC-1] 유사 스펙트럴 기반 최적제어 개요 (0) | 2021.12.15 |
| 오일러-라그랑지 방정식과 브라키스토크론 문제의 풀이 (0) | 2021.01.13 |




댓글