유사 스펙트럴(pseudospectral) 방법은 다음과 같이 경계조건을 갖는 미분방정식이 있을 때,
\[ \begin{align} & \mathcal{D} \mathbf{x}(t)=\mathbf{g}(t), \ \ \ \mathbf{x} \in V \subset \mathbb{R}^n \tag{1} \\ \\ & \mathcal{B} \mathbf{x}(t)=0, \ \ \ \mathbf{x} \in \partial V \end{align} \]
방정식의 미지해 \(\mathbf{x}(t)\) 를 다음과 같은 형식을 갖는 \(\mathbf{X}(t)\) 로 근사적으로 구하는 방법이다.
\[ \mathbf{x}(t) \approx \mathbf{X}(t)= \sum_{i=1}^N \mathbf{d}_i L_i (t) \tag{2} \]
위 식에서 \(N\) 개의 파라미터 \(\mathbf{d}_i\) 는 다음 식을 만족하도록 계산된다.
\[ \mathcal{D} \mathbf{X}(t_j ) = \sum_{i=1}^N \mathbf{d}_i \dot{L}_i (t_j) = \mathbf{g}(t_j ), \ \ \ j=1, ..., M \tag{3} \]
여기서 \(\mathcal{D}\) 는 미분, \(\mathcal{B}\) 는 경계조건을 뜻하는 연산자이고. \(L_i (t)\) 는 라그랑지 기저 다항식(Lagrange basis polynomial), \(N\) 은 라그랑지 다항식의 보간점(interpolating point) 갯수, \(M\) 은 콜로케이션 포인트(collocation point)의 갯수이다.
유사 스펙트럴 방법으로 다음 경계조건을 갖는 일차 미분방정식의 근사해를 구해보자.
\[ \begin{align} & \frac{dx}{dt}=-2t+\frac{1}{3}, \ \ \ t \in [-1, 1] \tag{4} \\ \\ & x(-1)= - \frac{1}{3} \end{align} \]
위 미분 방정식은 해석적으로 풀 수 있는데 정답은 다음과 같다.
\[ x(t)=1+\frac{t}{3}-t^2 \tag{5} \]
이제 3개의 보간점을 이용한 유사 스펙트럴 방법으로 근사해를 구해본다. 근사해는 식 (2)의 형식대로 다음과 같이 주어진다.
\[ x(t) \approx X(t)= \sum_{i=1}^3 d_i L_i (t) \tag{6} \]
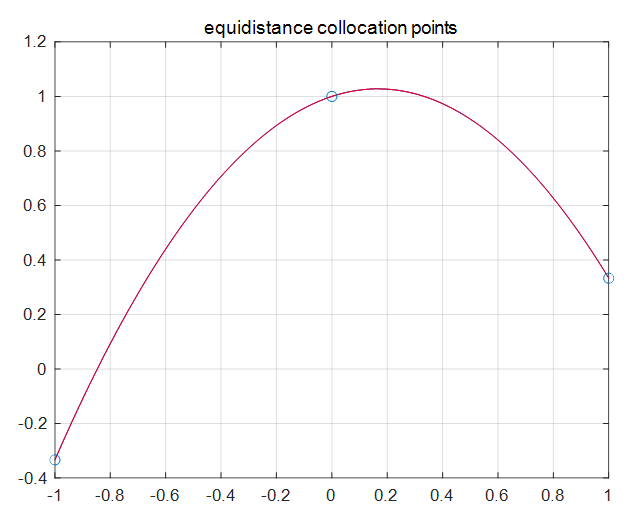
먼저 3개의 등간격(equidistance) 콜로케이션 포인트 \(t_1=-1, t_2=0, t_3=1\) 을 이용해 보자. 보간점은 콜로케이션 포인트와 일치시킨다. 그럼 각 콜로케이션 포인트에서는 식 (3)으로 주어진 대로 다음 미분 방정식을 만족해야 한다.
\[ \sum_{i=1}^3 d_i \dot{L}_i (t_j) =-2t_j+\frac{1}{3}, \ \ \ j=1, 2, 3 \tag{7} \]
위 식을 행렬식으로 풀어쓰면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} \dot{L}_1 (t_1) & \dot{L}_2 (t_1) & \dot{L}_3 (t_1) \\ \dot{L}_1 (t_2) & \dot{L}_2 (t_2) & \dot{L}_3 (t_2) \\ \dot{L}_1 (t_3) & \dot{L}_2 (t_3) & \dot{L}_3 (t_3)) \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix} \tag{8} \\ \\ & \ \ \ \ \ \ \ = \begin{bmatrix} -1.5 & 2 & -0.5 \\ -0.5 & 0 & 0.5 \\ 0.5 & -2 & 1.5 \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}= \begin{bmatrix} 7/3 \\ 1/3 \\ -5/3 \end{bmatrix} \end{align} \]
그리고 경계조건인 다음 식을 만족해야 한다.
\[ X(t_1 ) = - \frac{1}{3} = \sum_{i=1}^3 d_i L_i (t_1 ) =d_1 \tag{9} \]
식 (8)에서 역행렬은 존재하지 않는다. 하지만 경계조건에서 \(d_1=-1/3\) 임을 알고 있으므로 \(d_2=1, d_3=1/3\) 을 얻을 수 있다. 따라서 근사해는 다음 그림과 같이 되어서 해석적인 해와 일치한다.
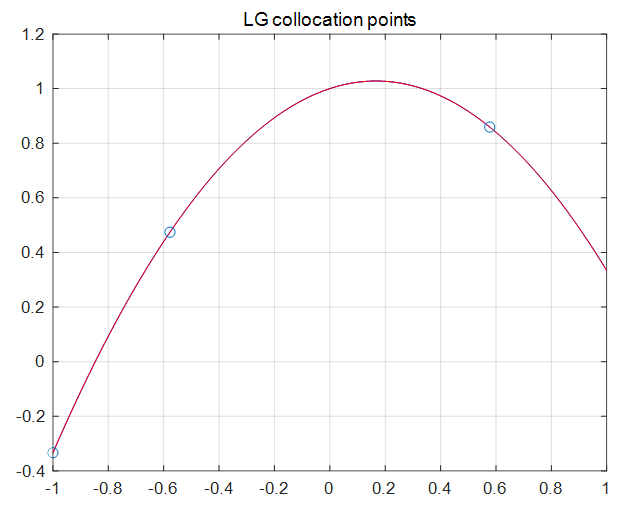
이번에는 2개의 LG(Legendre-Gauss) 콜로케이션 포인트 \(t_1=-0.5774, t_2=0.5774\) 를 이용해 보자. 보간점으로는 여기에 포인트 \(t_0=-1\) 을 추가한다. 그러면 각 콜로케이션 포인트에서는 다음 미분 방정식을 만족해야 한다.
\[ \sum_{i=0}^2 d_i \dot{L}_i (t_j) =-2t_j+\frac{1}{3}, \ \ \ j=1, 2 \tag{10} \]
위 식을 행렬식으로 풀어쓰면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} \dot{L}_0 (t_1) & \dot{L}_1 (t_1) & \dot{L}_2 (t_1) \\ \dot{L}_0 (t_2) & \dot{L}_1 (t_2) & \dot{L}_2 (t_2) \end{bmatrix} \begin{bmatrix} d_0 \\ d_1 \\ d_2 \end{bmatrix} \tag{11} \\ \\ & \ \ \ \ \ \ \ = \begin{bmatrix} -1.7321 & 1.5 & 0.2321 \\ 1.7321 & -3.2321 & 1.5 \end{bmatrix} \begin{bmatrix} d_0 \\ d_1 \\ d_2 \end{bmatrix}= \begin{bmatrix} 1.4880 \\ -0.8214 \end{bmatrix} \end{align} \]
그리고 경계조건인 다음 식을 만족해야 한다.
\[ X(t_0 )= - \frac{1}{3} = \sum_{i=0}^2 d_i L_i (t_0 ) =d_0 \tag{12} \]
\(d_0=-1/3\) 이므로 \(d_1=0.4742, d_2=0.859\) 를 얻을 수 있다. 따라서 근사해는 다음 그림과 같이 되어서 해석적인 해와 일치한다.
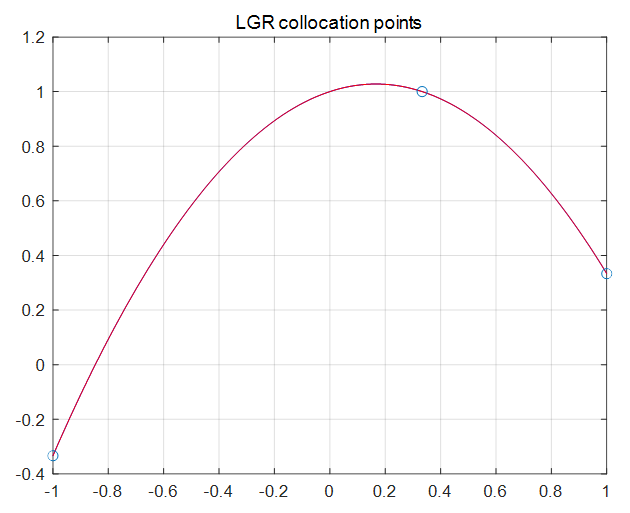
다음은 2개의 LGR (Legendre-Gauss-Radau) 콜로케이션 포인트 \(t_1=-1, t_2=0.3333\) 의 경우이다. 보간점으로는 여기에 포인트 \(t_3=1\) 을 추가한다. 그럼 각 콜로케이션 포인트에서는 다음 미분 방정식을 만족해야 한다.
\[ \sum_{i=1}^3 d_i \dot{L}_i (t_j) =-2t_j+\frac{1}{3}, \ \ \ j=1, 2 \tag{13} \]
위 식을 행렬식으로 풀어쓰면 다음과 같다.
\[ \begin{align} & \begin{bmatrix} \dot{L}_1 (t_1) & \dot{L}_2 (t_1) & \dot{L}_3 (t_1) \\ \dot{L}_1 (t_2) & \dot{L}_2 (t_2) & \dot{L}_3 (t_2) \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix} \tag{14} \\ \\ & \ \ \ \ \ \ \ = \begin{bmatrix} -1.25 & 2.25 & -1.0 \\ -0.25 & -0.75 & 1.0 \end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}= \begin{bmatrix} 7/3 \\ -1/3 \end{bmatrix} \end{align} \]
그리고 경계조건인 다음 식을 만족해야 한다.
\[ X(t_1 )=-\frac{1}{3} = \sum_{i=1}^3 d_i L_i (t_0 ) = d_1 \tag{15} \]
\(d_1=-1/3\) 이므로 \(d_2=1, d_3=1/3\) 을 얻을 수 있다. 따라서 근사해는 다음 그림과 같이 되어서 해석적인 해와 일치한다.
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [MPC] MPC를 위한 두가지 QP 모델 - 1 (0) | 2022.11.30 |
|---|---|
| [MPC] 모델예측제어 개요 (0) | 2022.11.28 |
| [PSOC-6] 유사 스펙트럴 방법 (Pseudospectral Method) (0) | 2022.04.23 |
| [PSOC-5] 가우시안 쿼드래처 (Gaussian Quadrature) (0) | 2021.12.18 |
| [PSOC-4] 라그랑지 보간 다항식 (0) | 2021.12.17 |




댓글