궤도 에너지와 속도

운동에너지(kinetic energy)와 위치에너지(potential energy)의 합이 기계적인 에너지 $\mathcal{E}$ 이며, 이 에너지는 운동 궤도상에서 일정하게 보존된다.

 

$$\begin{array}{}\text{(1)}& \frac{v^2}{2}-\frac{\mu }{r}=\mathcal{E}=\text{constant}\end{array}$$

 

여기서 $\frac{v^2}{2}$ 은 단위질량당 운동에너지, $-\frac{\mu }{r}$ 는 단위질량당 위치에너지이다.

 

 

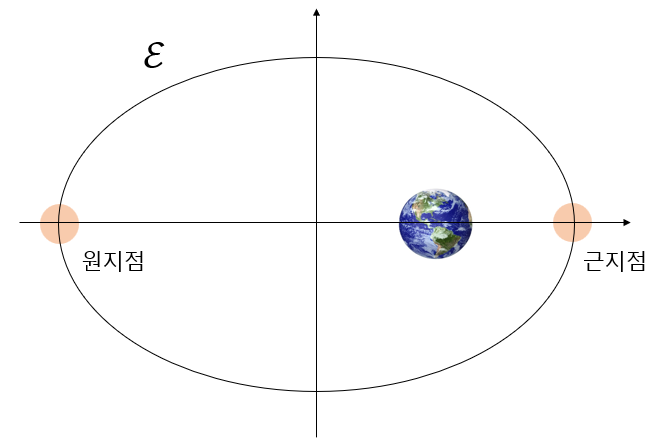
이제 이체문제(two-body problem)에서 질점 $M$ 을 지구로, 질점 $m$ 을 우주비행체로 보고 논의를 진행하자. 궤도의 에너지 $\mathcal{E}$ 는 궤도상에서 모두 동일하므로 근지점(perigee)이나 원지점(apogee)에서 에너지를 계산하는 것이 쉽다. 지구중심에 가장 근접한 지점을 근지점이라고 하고, 가장 먼 지점을 원지점이라고 한다.

 

 

원 궤도는 지구중심에서의 거리가 일정하기 때문에 근지점과 원지점이 따로 없다. 타원, 포물선, 쌍곡선 궤도에서 근지점 $r_p$ 는 실제 비행각이 $\theta =0$ 인 지점이 되며 아래 식과 같이 주어진다.

 

$$\begin{array}{}\text{(2)}& r_p=\frac{p}{1+e\cos 0}=\frac{p}{1+e}\end{array}$$

 

포물선 궤도는 $e=1$ 이므로 근지점의 거리는 $r_p=\frac{p}{2}$ 이다. 포물선 궤도를 제외한 모든 궤도에서 $p=a(1-e^2)$ 이므로 타원과 쌍곡선 궤도에서 위 식은 다음과 같이 쓸 수 있다.

 

$$\begin{array}{}\text{(3)}& r_p=\frac{p}{1+e}=\frac{a(1-e^2)}{1+e}=a(1-e)\end{array}$$

 

포물선과 쌍곡선 궤도의 경우 열린 궤도(open orbit)이므로 원지점까지의 거리는 무한대이다. 타원 궤도의 원지점 $r_a$ 는 $\theta ={180}^0$ 에서 다음과 같이 주어진다.

 

$$\begin{array}{}\text{(4)}& r_a=\frac{a(1-e^2)}{1+e\cos {180}^0}=\frac{a(1-e^2)}{1-e}=a(1+e)\end{array}$$

 

근지점과 원지점에서는 $\overrightarrow{r}$ 과 $\overrightarrow{v}$ 가 서로 직각이므로 각운동량 크기는 $h=r_p{v}_p=r_a{v}_a$ 가 된다. 여기서 $v_p$ 와 $v_a$ 는 각각 근지점과 원지점에서의 속도이다.

 

 

근지점에서 에너지는 식 (1)의 정의에 의하여

 

$$\begin{array}{}\text{(5)}& \mathcal{E}=\frac{v_p^2}{2}-\frac{\mu }{r_p}=\frac{h^2}{2r_p^2}-\frac{\mu }{r_p}\end{array}$$

 

가 된다. 포물선 궤도를 제외한 모든 궤도에서 $p=a(1-e^2)$ 이고 정의에 의하여 $h^2=\mu p$ 이며, 근지점의 거리는 식 (3)으로 주어지므로, 식 (5)의 에너지는

 

$$\begin{array}{r}\text{(6)}& \mathcal{E}& =\frac{\mu a(1-e^2)}{2a^2(1-e{)}^2}-\frac{\mu }{a(1-e)}\\ & =-\frac{\mu }{2a}\end{array}$$

 

가 된다. 포물선 궤도에서는 근지점의 거리가 $r_p=\frac{p}{2}$ 이므로 식 (5)에 대입하면,

 

$$\begin{array}{}\text{(7)}& \mathcal{E}=\frac{\mu p}{2(p/2{)}^2}-\frac{\mu }{(p/2)}=0\end{array}$$

 

이 된다. 식 (6)은 포물선 궤도를 제외한 조건에서 유도되었지만 포물선 궤도의 장반경의 길이를 $a=\mathrm{\infty }$ 라고 생각하면 식 (6)을 4개의 궤도 모두의 에너지 식으로 사용할 수가 있다.

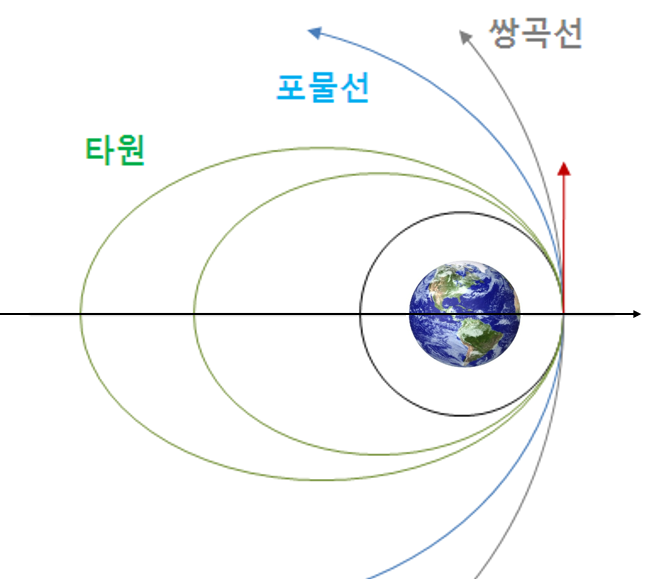
식 (6)에 의하면 궤도의 장반경은 에너지만의 함수임을 알 수 있다. 따라서 궤도의 장반경을 알 수 있다면 에너지를 계산할 수 있고, 궤도의 에너지를 알 수 있다면 궤도의 장반경을 계산할 수 있다. 또한 원과 타원 궤도와 같이 닫힌 궤도(closed orbit)의 경우 장반경은 $a>0$ 이므로 에너지는 $\mathcal{E}<0$ 이며, 포물선 궤도와 쌍곡선 궤도와 같이 열린 궤도(open orbit)의 경우 장반경은 $a=\mathrm{\infty }$ 이거나 $a<0$ 이므로 에너지는 $\mathcal{E}\ge 0$ 임을 알 수 있다.

 

 

궤도상에서 우주비행체의 속도를 식 (1)과 (6)을 이용하여 유도하면 다음과 같다.

 

$$\begin{array}{}\text{(8)}& v=\sqrt{2(\frac{\mu }{r}+\mathcal{E})}=\sqrt{\frac{2\mu }{r}-\frac{\mu }{a}}\end{array}$$

 

원 궤도는 궤도의 반지름이 $r=a$ 이므로

 

$$\begin{array}{}\text{(9)}& v_{circle}=\sqrt{\frac{\mu }{a}}\end{array}$$

 

이며, 포물선 궤도에서는 $\mathcal{E}=0$ 이므로 속도는

 

$$\begin{array}{}\text{(10)}& v_{parabola}=\sqrt{\frac{2\mu }{r}}\end{array}$$

 

이다.

한편 포물선 궤도에서 $r=\mathrm{\infty }$ 일 때 속도는 $v_{\mathrm{\infty }}=0$ 이지만 쌍곡선 궤도에서는 $v_{\mathrm{\infty }}=\sqrt{2\mathcal{E}}$ 임을 알 수 있다.

지구의 중력장을 벗어나려면 열린 궤도를 취해야 한다. 이때 우주비행체의 속도는 포물선 궤도를 따를 경우는 식 (10), 쌍곡선 궤도를 따를 경우는 식 (8)로 주어진다. 동일 위치 $r$ 에서의 속도를 비교해 보면 쌍곡선 궤도의 에너지가 $\mathcal{E}>0$ 이므로 항상 $v_{hyperbola}>v_{parabola}$ 이다. 따라서 지구 중력장을 벗어날 수 있는 최소의 속도, 즉 최소 지구탈출 속도는 포물선 궤도를 따를 때이며 그 속도는 $v_{escape}=\sqrt{\frac{2\mu }{r}}$ 이다.

 

 

지구의 표면에서의 지구탈출 속도를 계산해 보면

 

$$\begin{array}{}\text{(11)}& v_{escape}=\sqrt{\frac{2{\mu }_{earth}}{R_{earth}}}=11.18km/sec\end{array}$$

 

이다. 여기서 $R_{earth}$ 는 지구 반지름, ${\mu }_{earth}$ 는 지구의 중력 파라미터이다. 이 속도는 마하 $33$ 에 해당하는 엄청난 속도로 지구 중력장을 벗어나는 속도를 얻는 것이 불가능하게 생각될 정도다. 하지만 이 속도는 지구와 우주비행체 사이에 만유인력만 작용한다는 가정하에서 지표면에서 지구 중력장을 벗어나는데 필요한 초기 속도라는 것을 알아야 한다.

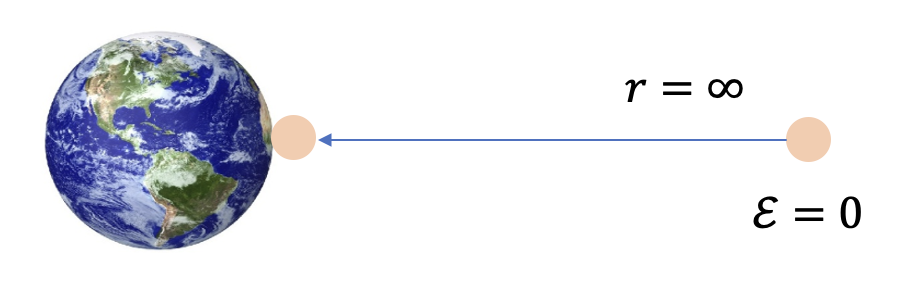
식 (8)의 속도는 에너지 보존법칙으로도 구할 수 있다. $r=\mathrm{\infty }$ 에서 속도가 $v_{\mathrm{\infty }}=0$ 인 물체가 지구 표면으로 떨어진다면 지표면에서의 속도는 식 (1)에 의해서 다음과 같이 계산할 수 있다.

 

$$\begin{array}{r}\text{(12)}& & \frac{v_{\mathrm{\infty }}^2}{2}-\frac{{\mu }_{earth}}{r_{\mathrm{\infty }}}=0=\frac{v_{escape}^2}{2}-\frac{{\mu }_{earth}}{R_{earth}}\\ & \to v_{escape}=\sqrt{\frac{2{\mu }_{earth}}{R_{earth}}}\end{array}$$

 

 

지표면에서의 지구탈출 속도를 제2우주속도라고도 한다. 그렇다면 제1우주속도는?

우주비행체가 지구의 표면에 추락하지 않고 지구의 중심을 기준으로 최소의 주기를 갖고 운동할 수 있는 속도를 제1우주속도라고 한다. 궤도의 주기는 다음 식으로 주어진다.

 

$$\begin{array}{}\text{(13)}& T=\frac{2\pi }{\sqrt{\mu }}{a}^{\frac{3}{2}}\end{array}$$

 

여기서 $a$ 는 원 궤도에서는 궤도의 반지름, 타원 궤도에서는 장반경의 길이이다. 최소 주기 운동을 하려면 이 값이 최소가 되어야 하는데, 이 값을 최소로 하면서 물체가 지구의 지표면에서 추락하지 않는 운동은 지구의 중심을 기준으로 지구의 반지름 $R_{earth}$ 을 반지름으로 하는 원 궤도 운동이다.

 

 

이 때의 속도는 식 (9)에 의해서 다음과 같이 계산할 수 있다.

 

$$\begin{array}{}\text{(14)}& v_c=\sqrt{\frac{{\mu }_{earth}}{R_{earth}}}=7.9km/sec\end{array}$$

 

식 (14)의 속도를 제1우주속도라고 한다. 이때의 주기는 식 (13)에 의해서 다음과 같이 주어진다.

 

$$\begin{array}{}\text{(15)}& T=\frac{2\pi }{\sqrt{{\mu }_{earth}}}{R}_{earth}^{\frac{3}{2}}=84.5min\end{array}$$

 

식 (15)로 주어지는 시간이 지표면에 추락하지 않고 지구를 1회전할 수 있는 최소 시간이다.