이체문제 가정하에서 다음과 같이 기본 궤도 미분 방정식을 유도한 바 있다.
\[ \frac{^id^2 \vec{r}}{dt^2} + \frac{\mu}{r^3} \vec{r} =0 \tag{1} \]
여기서 \(\mu=GM\) 은 중력 파라미터, \(\vec{r}\) 은 관성 좌표계 \(\{i\}\) 의 원점에서 질점 \(m\) 까지의 위치 벡터, \(r\)은 위치 벡터의 크기, 즉 거리다.
이 방정식에서 사용하는 거리와 시간의 크기는 \(km\) 나 초 (\(sec\))로 표시하기에는 너무 큰 경우가 많기 때문에 숫자의 크기를 줄이고 수치연산 시간을 줄이기 위해서 천문단위를 도입하여 사용하는 경우가 있다. 천문단위는 무차원화(nondimensionalization)된 시간과 거리 단위를 말한다.
먼저 기본 궤도 미분 방정식을 무차원화 해보자. 우선 기준 거리와 기준 시간을 각각 \(r_0\), \(t_0\) 로 두고 무차원화된 거리와 시간을 다음과 같은 기호로 표시한다.
\[ \tilde{\vec{r}} = \frac{\vec{r}}{r_0}, \ \ \ \tilde{r}= \frac{r}{r_0}, \ \ \ \tilde{t}= \frac{t}{t_0} \tag{2} \]
그리고 무차원화된 미분을 계산한다.
\[ \begin{align} & \frac{d\vec{r}}{dt} = \frac{d(r_0 \tilde{\vec{r}})}{d(t_0 \tilde{t})} = \frac{r_0}{t_0} \frac{d \tilde{\vec{r}}}{d \tilde{t}} \tag{3} \\ \\ & \frac{d^2 \vec{r}}{dt^2 }= \frac{d}{dt} \left( \frac{r_0}{t_0} \frac{d \tilde{\vec{r}}}{d \tilde{t}} \right) = \frac{r_0}{t_0^2 } \frac{ d}{d \tilde{t}} \left( \frac{d\tilde{\vec{r}}}{d\tilde{t}} \right) = \frac{r_0}{t_0^2 } \frac{d^2 \tilde{\vec{r}}}{d \tilde{t}^2 } \end{align} \]
식 (2)와 (3)을 식 (1)에 대입하여 운동방정식을 무차원화하면 다음과 같다.
\[ \frac{r_0}{t_0^2 } \frac{d^2 \tilde{\vec{r}}}{d \tilde{t}^2} + \frac{\mu}{r_0^3 \tilde{r}^3} r_0 \tilde{\vec{r}} = \frac{d^2 \tilde{\vec{r}}}{d \tilde{t}^2} + \frac{t_0^2}{r_0^3 } \frac{ \mu}{ \tilde{r}^3} \tilde{\vec{r}}=0 \tag{4} \]
여기서 \(\mu=GM\) 으로서 단위는 \(km^3/sec^2\) 이다. 이를 감안하여 기준 시간을
\[ t_0= \sqrt{ \frac{r_0^3}{\mu}} \tag{5} \]
로 정하면 식 (4)는 다음과 같이 된다.
\[ \frac{d^2 \tilde{\vec{r}}}{d \tilde{t}^2} + \frac{1}{ \tilde{r}^3} \tilde{\vec{r} }=0 \tag{6} \]
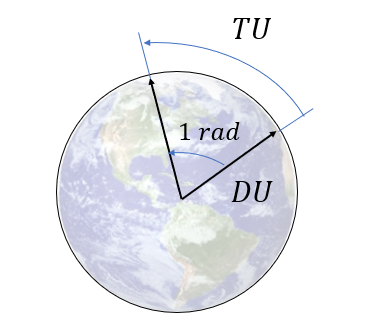
지구와 관련된 천문단위로서 기준 거리를 지구의 반지름으로 정의한다. 그러면 식 (5)에 의해서 기준 시간은 다음과 같이 된다.
\[ \begin{align} & r_0=DU=6378.137 \ km \tag{7} \\ \\ & t_0=TU= \sqrt{ \frac{DU^3}{\mu_{earth}}}=806.8 \ sec \approx 13.45 \ min \end{align} \]
여기서 \(DU\) 는 Distance Unit, \(TU\) 는 Time Unit을 뜻한다. 기준 시간 \(TU\) 는 반지름이 지구 반지름과 같은 원 궤도를 \(1 \ rad\) 만큼 움직이는데 걸리는 시간과 같다.
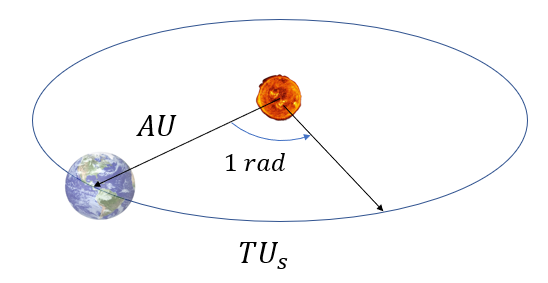
태양과 관련된 천문단위로는 기준 거리를 지구에서 태양까지의 평균 거리로 정의하고 기준 시간은 식 (5)로 정의한다.
\[ \begin{align} & r_0=AU=1.49598 \times 10^8 \ km \tag{8} \\ \\ & t_0=TU_s= \sqrt{ \frac{AU^3}{\mu_{sun} }} \approx 58.13282 \ days \end{align} \]
여기서 \(AU\) 는 Astronomical Unit을 뜻한다. 기준 시간 \(TU_s\) 는 반지름이 지구 공전 반지름과 같은 원 궤도를 \(1 \ rad\) 만큼 움직이는데 걸리는 시간과 같다.
'항공우주 > 우주역학' 카테고리의 다른 글
| ECEF 좌표계와 LLH 좌표계 (0) | 2021.12.30 |
|---|---|
| SCI 좌표계와 ECI 좌표계 (0) | 2021.12.30 |
| 궤도 에너지와 속도 (0) | 2021.12.14 |
| 케플러(Kepler) 법칙의 증명 (0) | 2021.12.13 |
| 이체문제에서 궤도의 모양 (0) | 2021.12.13 |




댓글